BBC BASIC, 570 514 490 bytes ASCII
Download interpreter at http://www.bbcbasic.co.uk/bbcwin/download.html
435 bytes tokenised
Full program displays an input from L.bmp on the screen, then modifies it to find a solution.
*DISPLAY L
t=PI/8q=FNa(1)
DEFFNa(n)IFn=7END
LOCALz,j,p,i,c,s,x,y,m,u,v
F.z=0TO99u=z MOD10*100v=z DIV10*100ORIGINu,v
F.j=0TO12S.4p=0F.i=j+3TOj+9S.2c=9*COS(i*t)s=9*SIN(i*t)p=p*4-(POINT(c,s)<>0)*2-(POINT(9*c,9*s)<>0)N.
m=n:IFn=5A.(43A.p)=0p=0m=7
IF(ASCM."??O|(C",n)-64A.p)=0THEN
F.i=-1TO0GCOL0,-i*n:c=99*COS(j*t)s=99*SIN(j*t)y=402/3^m MOD3-1MOVE-c-s*y,c*y-s:x=n<3MOVEc*x-s*x,s*x+c*x:x=2778/3^m MOD3-1y=5775/3^m MOD3-1PLOT85-32*(n MOD6>3),c*x-s*y,s*x+c*y:IFi q=FNa(n+1)ORIGINu,v
N.
ENDIF
N.N.=0
Explanation
Note that in BBC basic a distance of 1 pixel = 2 units, so the 50x50 pixel grid becomes a 100x100 grid.
We use a recursive function to place the 2 large triangles, medium triangle, square and parallelogram into the shape. The earlier shape in the list is drawn before the next recursive call is made. if a recursive call returns without finding a solution, the earlier shape is overdrawn in black and a new position of the earlier shape is tried.
Once these five shapes are drawn, placing the two small triangles is just a formality. It is necessary to draw one of them though, in order to distiguish them if they share a common edge. We only colour one of the two small triangles. The other is left in natural black.
Placing of each shape is attempted at different x,y coordinates and in 4 different rotations. To test if there is free space to draw a shape we use the template below, with 45 degree angles. The rotations are made about the * and the 8 pixels tested are in 2 semicircles of radius 9 and 81 units and fall on radiating lines at odd multiples of 22.5 degrees to the x and y axes.
For a large triangle all 8 spaces are required to be clear. For other shapes only some of the cells must be clear so a mask is applied.
+----+---- Shape Mask HGFEDCBA Mask decimal
|\ E/|\G /
| \/F|H\/ 1,2. Large triangle 11111111 -1
|C/\ | / 3. Med triangle 00001111 15
|/ D\|/ 4. Square 00111100 60
+----* 5. Parallelogram 11101000 -24
|\ B/ 6. Small triangle 00000011 3
|A\/ 7. Parallogr reversed 00101011 43
| / Note: reversed parallelogram is checked/drawn at recursion depth n=5
|/ with a special check, but the coordinates are encoded as m=7.
Once it is established that a shape will fit, it must be drawn. If it is a triangle it is plotted with PLOT 85, if it is a parallelogram, the number is 32 higher (note that for PLOT purposes we consider a square a special parallelogram). In either case 3 consecutive vertices must be given. The second vertex is the origin of the shape (marked * in the above table) except in the case of the large triangle, where (prior to rotation) it is -1,-1. The other 2 vertices can have x and y coordinates of -1,0 or 1 which are extracted from base 3 encoded numbers, then scaled by 99 and rotated as necessary by transformation with c and s.
Ungolfed code
*DISPLAY L
t=PI/8 :REM Constant 22.5 degrees.
q=FNa(1) :REM Call function, return dummy value to q
END :REM End the program gracefully if no solution. Absent in golfed version.
DEFFNa(n) :REM Recursive function to place shapes.
IFn=7END :REM If n=7 solution found, end program.
LOCALk,z,j,p,i,c,s,x,y,m,u,v :REM declare local variables for function.
k=ASCMID$("??O|(C",n)-64 :REM Bitmasks for big tri, big tri, med tri, sq, normal paralellogram, small tri.
FORz=0TO99 :REM For each point on the grid
u=z MOD10*100:v=z DIV10*100 :REM calculate its x and y coordinates relative to bottom left of screen
ORIGINu,v :REM and set the origin to this point.
FORj=0TO12STEP4 :REM For each rotation 0,90,180,270deg
p=0 :REM assume no non-black pixels found
FORi=j+3TOj+9STEP2 :REM test angles of 3,5,7,9 times 22.5 deg anticlockwise from right x axis.
c=9*COS(i*t) :REM Coords of test points at radius ll
s=9*SIN(i*t)
p*=4 :REM Leftshift any existing data in p
p-=(POINT(c,s)<>0)*2+(POINT(9*c,9*s)<>0) :REM and check pixels at radius 11 and 99.
NEXT
m=n :REM The index of the shape to plot normally corresponds with recursion depth n.
IF n=5 AND (43ANDp)=0 p=0:m=7 :REM If n=5 check if a reverse parallelogram is possible (mask 43). If so, clear p and change m to 7.
REM :REM Check p against mask k, if the shape fits then...
IF (k ANDp)=0 THEN
FOR i=-1 TO 0 :REM draw the shape in colour, and if deeper recursions prove unsuccesful, redraw it in black.
GCOL0,-i*n :REM Colour is equal to n.
c=99*COS(j*t) :REM Set parameters c and s for scaling by 99
s=99*SIN(j*t) :REM and rotation by 0,90,180 or 270 as appropriate.
x=-1 :REM For vertex 1, x=-1 always.
y=402/3^m MOD3-1 :REM Lookup y value for vertex 1.
MOVEc*x-s*y,s*x+c*y :REM Use c and s to transform the vertex and move to it.
x=n<3 :REM For vertex 2, coords are 0,0 except for large triangle where they are -1,-1
y=x :REM in BBC BASIC, TRUE=-1
MOVEc*x-s*y,s*x+c*y :REM Use c and s to transform the vertex and move to it.
x=2778/3^m MOD3-1 :REM Lookup x and y value for vertex 3.
y=5775/3^m MOD3-1 :REM PLOT85 uses last 2 points + specified point to make triangle, PLOT85+32 makes paralelogram (or square.)
PLOT85-32*(n MOD6>3),c*x-s*y,s*x+c*y :REM Use c and s to transform the vertex and draw shape.
IFi q=FNa(n+1):ORIGINu,v :REM If i=-1 recurse to next level. If it fails, reset the origin before replotting this level's shape in black.
NEXT
ENDIF
NEXT
NEXT
=0 :REM Dummy value to return from function
Output
This is a montage of the solutions found by the program for the test cases. Use of 99 instead of 100 for golfing reasons leaves some small black gaps. As the shapes are redrawn during the searches, it can take a few seconds to run for some cases, and is quite fascinating to watch.
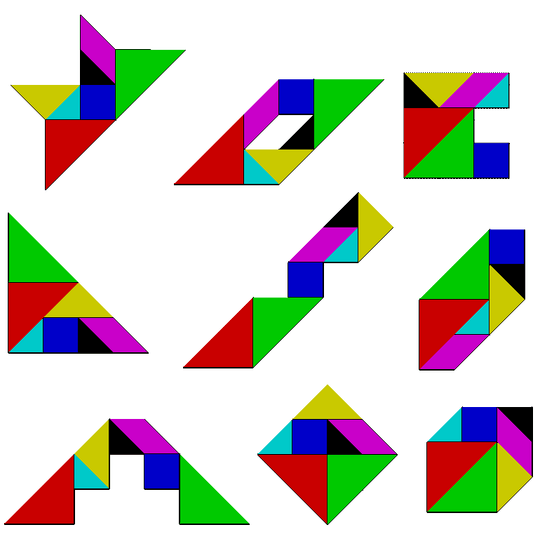
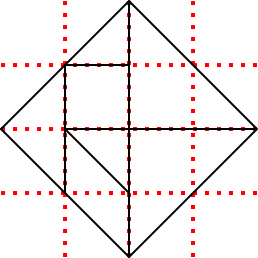












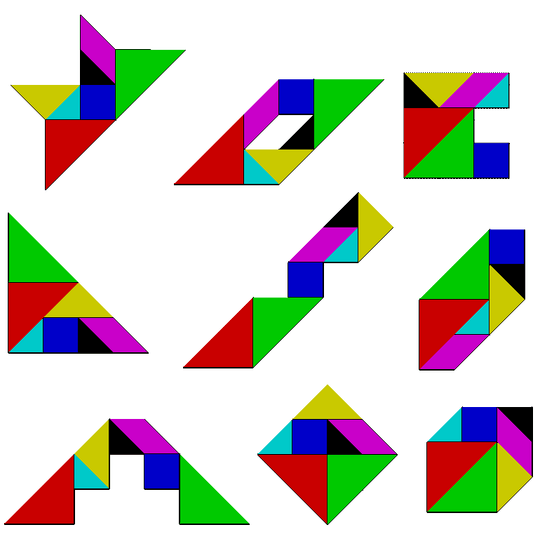
image processing is an entirely unnecessary hurdle in this challenge. I'd find it much more appealing if you just specified the input as a small binary array. – Sparr – 2016-09-10T22:00:38.943
I did consider that when the challenge was in the sandbox, but the majority thought that an input and output that is "human readable" is more appealing. But you have enough room to sample the images yourself. – flawr – 2016-09-10T22:05:45.530
I would've been more interested if, as flawr said, there was a more flexible input format. – Magic Octopus Urn – 2016-09-12T21:05:00.427
What do you consider as the big hurdle here? I think you can easily read, e.g. every 25th pixel, with an offset of 12 pixels to get e.g. a binary image with one pixel per "section". As I see it, reading the input is the smallest of all the problems, as the input is strictly defined. The real challenge is the computation itself. – flawr – 2016-09-12T21:29:17.900
I think that's the very objection: If reading the image isn't part of "the real challenge," why is it part of the task at all? It's tedious and adds a lot of bytes—and that's assuming someone's language of choice can even read images. – Jordan – 2016-09-13T15:37:38.723
1As I said, that was discussed when it was in the sandbox. But I doubt that it does add a lot of bytes, as the task itself is a lot more difficult. – flawr – 2016-09-13T15:56:30.573
3I was one of the people who recommended that the input and output be the way they are, and I made that recommendation because this is, in my opinion, the most natural and fitting way to present a Tangram challenge. Any form of input/output would take a significant number of bytes, so I don't think that's really an issue here. – El'endia Starman – 2016-09-13T16:20:53.517
1
I agree with Elendia. The only problem with graphical I/O is that it could limit languages that don't have graphics facilities. That said, PBM and PGM are so close to ASCII art that there is no real problem, IF it is the case that people are aware of such formats. https://en.wikipedia.org/wiki/Netpbm_format
– Level River St – 2016-09-14T00:14:56.5701@LevelRiverSt That is a good point, I think it would be totally accepptable to use those formats or even e.g. a 2d array/string of zeros and ones. – flawr – 2016-09-14T08:19:33.000