Funciton, non-competitive
UPDATE! Massive performance improvement! n = 7 now completes in under 10 minutes! See explanation at bottom!
This was good fun to write. This is a brute-force solver for this problem written in Funciton. Some factoids:
- It accepts an integer on STDIN. Any extraneous whitespace breaks it, including a newline after the integer.
- It uses the numbers 0 to n − 1 (not 1 to n).
- It fills the grid “backwards”, so you get a solution where the bottom row reads
3 2 1 0 rather than where the top row reads 0 1 2 3.
- It correctly outputs
0 (the only solution) for n = 1.
- Empty output for n = 2 and n = 3.
- When compiled to an exe, takes about 8¼ minutes for n = 7 (was about one hour before the performance improvement). Without compiling (using the interpreter) it takes about 1.5 times as long, so using the compiler is worth it.
- As a personal milestone, this is the first time I wrote a whole Funciton program without first writing the program in a pseudocode language. I did write it in actual C# first though.
- (However, this is not the first time I made a change to massively improve the performance of something in Funciton. The first time I did that was in the factorial function. Swapping the order of the operands of the multiplication made a huge difference because of how the multiplication algorithm works. Just in case you were curious.)
Without further ado:
┌────────────────────────────────────┐ ┌─────────────────┐
│ ┌─┴─╖ ╓───╖ ┌─┴─╖ ┌──────┐ │
│ ┌─────────────┤ · ╟─╢ Ӂ ╟─┤ · ╟───┤ │ │
│ │ ╘═╤═╝ ╙─┬─╜ ╘═╤═╝ ┌─┴─╖ │ │
│ │ └─────┴─────┘ │ ♯ ║ │ │
│ ┌─┴─╖ ╘═╤═╝ │ │
│ ┌────────────┤ · ╟───────────────────────────────┴───┐ │ │
┌─┴─╖ ┌─┴─╖ ┌────╖ ╘═╤═╝ ┌──────────┐ ┌────────┐ ┌─┴─╖│ │
│ ♭ ║ │ × ╟───┤ >> ╟───┴───┘ ┌─┴─╖ │ ┌────╖ └─┤ · ╟┴┐ │
╘═╤═╝ ╘═╤═╝ ╘══╤═╝ ┌─────┤ · ╟───────┴─┤ << ╟─┐ ╘═╤═╝ │ │
┌───────┴─────┘ ┌────╖ │ │ ╘═╤═╝ ╘══╤═╝ │ │ │ │
│ ┌─────────┤ >> ╟─┘ │ └───────┐ │ │ │ │ │
│ │ ╘══╤═╝ ┌─┴─╖ ╔═══╗ ┌─┴─╖ ┌┐ │ │ ┌─┴─╖ │ │
│ │ ┌┴┐ ┌───────┤ ♫ ║ ┌─╢ 0 ║ ┌─┤ · ╟─┤├─┤ ├─┤ Ӝ ║ │ │
│ │ ╔═══╗ └┬┘ │ ╘═╤═╝ │ ╚═╤═╝ │ ╘═╤═╝ └┘ │ │ ╘═╤═╝ │ │
│ │ ║ 1 ╟───┬┘ ┌─┴─╖ └───┘ ┌─┴─╖ │ │ │ │ │ ┌─┴─╖ │
│ │ ╚═══╝ ┌─┴─╖ │ ɓ ╟─────────────┤ ? ╟─┘ │ ┌─┴─╖ │ ├─┤ · ╟─┴─┐
│ ├─────────┤ · ╟─┐ ╘═╤═╝ ╘═╤═╝ ┌─┴────┤ + ╟─┘ │ ╘═╤═╝ │
┌─┴─╖ ┌─┴─╖ ╘═╤═╝ │ ╔═╧═╕ ╔═══╗ ┌───╖ ┌─┴─╖ ┌─┴─╖ ╘═══╝ │ │ │
┌─┤ · ╟─┤ · ╟───┐ └┐ └─╢ ├─╢ 0 ╟─┤ ⌑ ╟─┤ ? ╟─┤ · ╟──────────────┘ │ │
│ ╘═╤═╝ ╘═╤═╝ └───┐ ┌┴┐ ╚═╤═╛ ╚═╤═╝ ╘═══╝ ╘═╤═╝ ╘═╤═╝ │ │
│ │ ┌─┴─╖ ┌───╖ │ └┬┘ ┌─┴─╖ ┌─┘ │ │ │ │
│ ┌─┴───┤ · ╟─┤ Җ ╟─┘ └────┤ ? ╟─┴─┐ ┌─────────────┘ │ │
│ │ ╘═╤═╝ ╘═╤═╝ ╘═╤═╝ │ │╔════╗╔════╗ │ │
│ │ │ ┌──┴─╖ ┌┐ ┌┐ ┌─┴─╖ ┌─┴─╖ │║ 10 ║║ 32 ║ ┌─────────────────┘ │
│ │ │ │ << ╟─┤├─┬─┤├─┤ · ╟─┤ · ╟─┘╚══╤═╝╚╤═══╝ ┌──┴──┐ │
│ │ │ ╘══╤═╝ └┘ │ └┘ ╘═╤═╝ ╘═╤═╝ │ ┌─┴─╖ ┌─┴─╖ ┌─┴─╖ │
│ │ ┌─┴─╖ ┌─┴─╖ ┌─┴─╖ ┌─┴─╖ ╔═╧═╕ └─┤ ? ╟─┤ · ╟─┤ % ║ │
│ └─────┤ · ╟─┤ · ╟──┤ Ӂ ╟──┤ ɱ ╟─╢ ├───┐ ╘═╤═╝ ╘═╤═╝ ╘═╤═╝ │
│ ╘═╤═╝ ╘═╤═╝ ╘═╤═╝ ╘═══╝ ╚═╤═╛ ┌─┴─╖ ┌─┴─╖ │ └────────────────────┘
│ └─────┤ │ └───┤ ‼ ╟─┤ ‼ ║ │ ┌──────┐
│ │ │ ╘═══╝ ╘═╤═╝ │ │ ┌────┴────╖
│ │ │ ┌─┴─╖ │ │ │ str→int ║
│ │ └──────────────────────┤ · ╟───┴─┐ │ ╘════╤════╝
│ │ ┌─────────╖ ╘═╤═╝ │ ╔═╧═╗ ┌──┴──┐
│ └──────────┤ int→str ╟──────────┘ │ ║ ║ │ ┌───┴───┐
│ ╘═════════╝ │ ╚═══╝ │ │ ┌───╖ │
└───────────────────────────────────────────────────────┘ │ └─┤ × ╟─┘
┌──────────────┐ ╔═══╗ │ ╘═╤═╝
╔════╗ │ ╓───╖ ┌───╖ │ ┌───╢ 0 ║ │ ┌─┴─╖ ╔═══╗
║ −1 ║ └─╢ Ӝ ╟─┤ × ╟──┴──────┐ │ ╚═╤═╝ └───┤ Ӂ ╟─╢ 0 ║
╚═╤══╝ ╙───╜ ╘═╤═╝ │ │ ┌─┴─╖ ╘═╤═╝ ╚═══╝
┌─┴──╖ ┌┐ ┌───╖ ┌┐ ┌─┴──╖ ╔════╗ │ │ ┌─┤ ╟───────┴───────┐
│ << ╟─┤├─┤ ÷ ╟─┤├─┤ << ║ ║ −1 ║ │ │ │ └─┬─╜ ┌─┐ ┌─────┐ │
╘═╤══╝ └┘ ╘═╤═╝ └┘ ╘═╤══╝ ╚═╤══╝ │ │ │ └───┴─┘ │ ┌─┴─╖ │
│ └─┘ └──────┘ │ │ └───────────┘ ┌─┤ ? ╟─┘
└──────────────────────────────┘ ╓───╖ └───────────────┘ ╘═╤═╝
┌───────────╢ Җ ╟────────────┐ │
┌────────────────────────┴───┐ ╙───╜ │
│ ┌─┴────────────────────┐ ┌─┴─╖
┌─┴─╖ ┌─┴─╖ ┌─┴─┤ · ╟──────────────────┐
│ ♯ ║ ┌────────────────────┤ · ╟───────┐ │ ╘═╤═╝ │
╘═╤═╝ │ ╘═╤═╝ │ │ │ ┌───╖ │
┌─────┴───┘ ┌─────────────────┴─┐ ┌───┴───┐ ┌─┴─╖ ┌─┴─╖ ┌─┤ × ╟─┴─┐
│ │ ┌─┴─╖ │ ┌───┴────┤ · ╟─┤ · ╟──────────┤ ╘═╤═╝ │
│ │ ┌───╖ ┌───╖ ┌──┤ · ╟─┘ ┌─┴─┐ ╘═╤═╝ ╘═╤═╝ ┌─┴─╖ │ │
│ ┌────┴─┤ ♭ ╟─┤ × ╟──┘ ╘═╤═╝ │ ┌─┴─╖ ┌───╖└┐ ┌──┴─╖ ┌─┤ · ╟─┘ │
│ │ ╘═══╝ ╘═╤═╝ ┌───╖ │ │ │ × ╟─┤ Ӝ ╟─┴─┤ ÷% ╟─┐ │ ╘═╤═╝ ┌───╖ │
│ ┌─────┴───┐ ┌────┴───┤ Ӝ ╟─┴─┐ │ ╘═╤═╝ ╘═╤═╝ ╘══╤═╝ │ │ └───┤ Ӝ ╟─┘
│ ┌─┴─╖ ┌───╖ │ │ ┌────╖ ╘═╤═╝ │ └───┘ ┌─┴─╖ │ │ └────┐ ╘═╤═╝
│ │ × ╟─┤ Ӝ ╟─┘ └─┤ << ╟───┘ ┌─┴─╖ ┌───────┤ · ╟───┐ │ ┌─┴─╖ ┌───╖ │ │
│ ╘═╤═╝ ╘═╤═╝ ╘══╤═╝ ┌───┤ + ║ │ ╘═╤═╝ ├──┴─┤ · ╟─┤ × ╟─┘ │
└───┤ └────┐ ╔═══╗ ┌─┴─╖ ┌─┴─╖ ╘═╤═╝ │ ╔═══╗ ┌─┴─╖ ┌─┴─╖ ╘═╤═╝ ╘═╤═╝ │
┌─┴─╖ ┌────╖ │ ║ 0 ╟─┤ ? ╟─┤ = ║ ┌┴┐ │ ║ 0 ╟─┤ ? ╟─┤ = ║ │ │ ┌────╖ │
│ × ╟─┤ << ╟─┘ ╚═══╝ ╘═╤═╝ ╘═╤═╝ └┬┘ │ ╚═══╝ ╘═╤═╝ ╘═╤═╝ │ └─┤ << ╟─┘
╘═╤═╝ ╘═╤══╝ ┌┐ ┌┐ │ │ └───┘ ┌─┴─╖ ├──────┘ ╘═╤══╝
│ └────┤├──┬──┤├─┘ ├─────────────────┤ · ╟───┘ │
│ └┘┌─┴─╖└┘ │ ┌┐ ┌┐ ╘═╤═╝ ┌┐ ┌┐ │
└────────────┤ · ╟─────────┘ ┌─┤├─┬─┤├─┐ └───┤├─┬─┤├────────────┘
╘═╤═╝ │ └┘ │ └┘ │ └┘ │ └┘
└───────────────┘ │ └────────────┘
Explanation of the first version
The first version took about an hour to solve n = 7. The following explains mostly how this slow version worked. At the bottom I will explain what change I made to get it to under 10 minutes.
An excursion into bits
This program needs bits. It needs lots of bits, and it needs them in all the right places. Experienced Funciton programmers already know that if you need n bits, you can use the formula

which in Funciton can be expressed as

When doing my performance optimization, it occurred to me that I can calculate the same value much faster using this formula:

I hope you’ll forgive me that I didn’t update all the equation graphics in this post accordingly.
Now, let’s say you don’t want a contiguous block of bits; in fact, you want n bits at regular intervals every k-th bit, like so:
LSB
↓
00000010000001000000100000010000001
└──┬──┘
k
The formula for this is fairly straight-forward once you know it:

In the code, the function Ӝ takes values n and k and calculates this formula.
Keeping track of used numbers
There are n² numbers in the final grid, and each number can be any of n possible values. In order to keep track of which numbers are permitted in each cell, we maintain a number consisting of n³ bits, in which a bit is set to indicate that a particular value is taken. Initially this number is 0, obviously.
The algorithm begins in the bottom-right corner. After “guessing” the first number is a 0, we need to keep track of the fact that the 0 is no longer permitted in any cell along the same row, column and diagonal:
LSB (example n=5)
↓
10000 00000 00000 00000 10000
00000 10000 00000 00000 10000
00000 00000 10000 00000 10000
00000 00000 00000 10000 10000
10000 10000 10000 10000 10000
↑
MSB
To this end, we calculate the following four values:
Current row: We need n bits every n-th bit (one per cell), and then shift it to the current row r, remembering every row contains n² bits:

Current column: We need n bits every n²-th bit (one per row), and then shift it to the current column c, remembering every column contains n bits:

Forward diagonal: We need n bits every... (did you pay attention? Quick, figure it out!)... n(n+1)-th bit (well done!), but only if we’re actually on the forward diagonal:
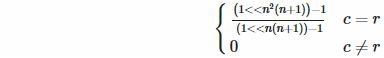
Backward diagonal: Two things here. First, how do we know if we’re on the backward diagonal? Mathematically, the condition is c = (n − 1) − r, which is the same as c = n + (−r − 1). Hey, does that remind you of something? That’s right, it’s two’s complement, so we can use bitwise negation (very efficient in Funciton) instead of the decrement. Second, the formula above assumes that we want the least significant bit to be set, but in the backward diagonal we don’t, so we have to shift it up by... do you know?... That’s right, n(n − 1).
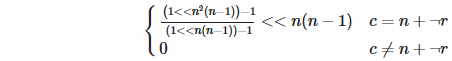
This is also the only one where we potentially divide by 0 if n = 1. However, Funciton doesn’t care. 0 ÷ 0 is just 0, don’t you know?
In the code, the function Җ (the bottom one) takes n and an index (from which it calculates r and c by division and remainder), calculates these four values and ors them together.
The brute-force algorithm
The brute-force algorithm is implemented by Ӂ (the function at the top). It takes n (the grid size), index (where in the grid we’re currently placing a number), and taken (the number with n³ bits telling us which numbers we can still place in each cell).
This function returns a sequence of strings. Each string is a full solution to the grid. It’s a complete solver; it would return all solutions if you let it, but it returns them as a lazy-evaluated sequence.
If index has reached 0, we’ve successfully filled the whole grid, so we return a sequence containing the empty string (a single solution that covers none of the cells). The empty string is 0, and we use the library function ⌑ to turn that into a single-element sequence.
The check described under performance improvement below happens here.
If index has not yet reached 0, we decrement it by 1 to get the index at which we now need to place a number (call that ix).
We use ♫ to generate a lazy sequence containing the values from 0 to n − 1.
Then we use ɓ (monadic bind) with a lambda that does the following in order:
- First look at the relevant bit in taken to decide whether the number is valid here or not. We can place a number i if and only if taken & (1 << (n × ix) << i) isn’t already set. If it is set, return
0 (empty sequence).
- Use
Җ to calculate the bits corresponding to the current row, column and diagonal(s). Shift it by i and then or it onto taken.
- Recursively call
Ӂ to retrieve all solutions for the remaining cells, passing it the new taken and the decremented ix. This returns a sequence of incomplete strings; each string has ix characters (the grid filled in up to index ix).
- Use
ɱ (map) to go through the solutions thusly found and use ‼ to concatenate i to the end of each. Append a newline if index is a multiple of n, otherwise a space.
Generating the result
The main program calls Ӂ (the brute forcer) with n, index = n² (remember we fill the grid backwards) and taken = 0 (initially nothing is taken). If the result of this is an empty sequence (no solution found), output the empty string. Otherwise, output the first string in the sequence. Note that this means it will evaluate only the first element of the sequence, which is why the solver doesn’t continue until it has found all solutions.
Performance improvement
(For those who already read the old version of the explanation: the program no longer generates a sequence of sequences that needs to be separately turned into a string for output; it just generates a sequence of strings directly. I’ve edited the explanation accordingly. But that wasn’t the main improvement. Here it comes.)
On my machine, the compiled exe of the first version took pretty much exactly 1 hour to solve n = 7. This was not within the given time limit of 10 minutes, so I didn’t rest. (Well, actually, the reason I didn’t rest was because I had this idea on how to massively speed it up.)
The algorithm as described above stops its search and backtracks every time that it encounters a cell in which all the bits in the taken number are set, indicating that nothing can be put into this cell.
However, the algorithm will continue to futilely fill the grid up to the cell in which all those bits are set. It would be much faster if it could stop as soon as any yet-to-be-filled-in cell already has all the bits set, which already indicates that we can never solve the rest of the grid no matter what numbers we put in it. But how do you efficiently check whether any cell has its n bits set without going through all of them?
The trick starts by adding a single bit per cell to the taken number. Instead of what was shown above, it now looks like this:
LSB (example n=5)
↓
10000 0 00000 0 00000 0 00000 0 10000 0
00000 0 10000 0 00000 0 00000 0 10000 0
00000 0 00000 0 10000 0 00000 0 10000 0
00000 0 00000 0 00000 0 10000 0 10000 0
10000 0 10000 0 10000 0 10000 0 10000 0
↑
MSB
Instead of n³, there are now n²(n + 1) bits in this number. The function that populates the current row/column/diagonal has been changed accordingly (actually, completely rewritten to be honest). That function will still populate only n bits per cell though, so the extra bit we just added will always be 0.
Now, let’s say we are halfway through the calculation, we just placed a 1 in the middle cell, and the taken number looks something like this:
current
LSB column (example n=5)
↓ ↓
11111 0 10010 0 01101 0 11100 0 11101 0
00011 0 11110 0 01101 0 11101 0 11100 0
11111 0 11110 0[11101 0]11100 0 11100 0 ← current row
11111 0 11111 0 11111 0 11111 0 11111 0
11111 0 11111 0 11111 0 11111 0 11111 0
↑
MSB
As you can see, the top-left cell (index 0) and the middle-left cell (index 10) are now impossible. How do we most efficiently determine this?
Consider a number in which the 0th bit of each cell is set, but only up to the current index. Such a number is easy to calculate using the familiar formula:

What would we get if we added these two numbers together?
LSB LSB
↓ ↓
11111 0 10010 0 01101 0 11100 0 11101 0 10000 0 10000 0 10000 0 10000 0 10000 0 ╓───╖
00011 0 11110 0 01101 0 11101 0 11100 0 ║ 10000 0 10000 0 10000 0 10000 0 10000 0 ║
11111 0 11110 0 11101 0 11100 0 11100 0 ═══╬═══ 10000 0 10000 0 00000 0 00000 0 00000 0 ═════ ╓─╜
11111 0 11111 0 11111 0 11111 0 11111 0 ║ 00000 0 00000 0 00000 0 00000 0 00000 0 ═════ ╨
11111 0 11111 0 11111 0 11111 0 11111 0 00000 0 00000 0 00000 0 00000 0 00000 0 o
↑ ↑
MSB MSB
The result is:
OMG
↓
00000[1]01010 0 11101 0 00010 0 00011 0
10011 0 00001 0 11101 0 00011 0 00010 0
═════ 00000[1]00001 0 00011 0 11100 0 11100 0
═════ 11111 0 11111 0 11111 0 11111 0 11111 0
11111 0 11111 0 11111 0 11111 0 11111 0
As you can see, the addition overflows into the extra bit that we added, but only if all the bits for that cell are set! Therefore, all that’s left to do is to mask out those bits (same formula as above, but << n) and check if the result is 0:
00000[1]01010 0 11101 0 00010 0 00011 0 ╓╖ 00000 1 00000 1 00000 1 00000 1 00000 1 ╓─╖ ╓───╖
10011 0 00001 0 11101 0 00011 0 00010 0 ╓╜╙╖ 00000 1 00000 1 00000 1 00000 1 00000 1 ╓╜ ╙╖ ║
00000[1]00001 0 00011 0 11100 0 11100 0 ╙╥╥╜ 00000 1 00000 1 00000 0 00000 0 00000 0 ═════ ║ ║ ╓─╜
11111 0 11111 0 11111 0 11111 0 11111 0 ╓╜╙╥╜ 00000 0 00000 0 00000 0 00000 0 00000 0 ═════ ╙╖ ╓╜ ╨
11111 0 11111 0 11111 0 11111 0 11111 0 ╙──╨─ 00000 0 00000 0 00000 0 00000 0 00000 0 ╙─╜ o
If it is not zero, the grid is impossible and we can stop.
- Screenshot showing solution and running time for n = 4 to 7.






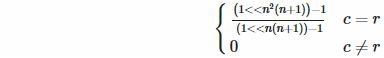
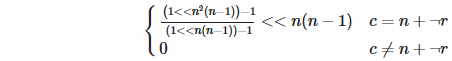

1Related, but such a grid won't work here because of the diagonals requirement. – xnor – 2015-12-20T00:57:28.987
I like this challenge but I can't figure out an algorithm for even values of
N. This JavaScript code works forN = 1, 5 or 7though if it helps anyone:for(o="",y=N;y--;o+="\n")for(x=N;x--;)o+=(((N-y)*2+x)%N)+1– user81655 – 2015-12-20T07:01:42.543Very related, possible duplicate: http://codegolf.stackexchange.com/q/47846/15599
– Level River St – 2015-12-20T07:49:03.967@steveverrill That wasn't code golf though. – randomra – 2015-12-20T08:12:45.813
@steveverrill, although the title made it seem that that should be a duplicate, the question was actually asking for something different to the title. I've corrected the title. – Peter Taylor – 2015-12-20T09:01:56.810
@PeterTaylor I'd never heard of a greco-latin square, but it's basically just 2 superimposed latin squares. The biggest difference seems to be that the other question requires all wrapped diagonals to contain every number, whereas this one only requires the two main diagonals to contain every number. Hence this one has a solution for N=4 but the other one doesn't. – Level River St – 2015-12-20T09:09:43.453
Do we have to output the solution almost exactly like in your examples, or can we for example return a list of lists containing the values? – Fatalize – 2015-12-20T14:43:57.297
@Fatalize each line of your output should be one row of the board your code generated. The line can be formatted however you want. – hargasinski – 2015-12-20T15:43:38.227
1Maybe you should be more explicit about the
N = 1case: answers that aim for the bonus should return1, not the empty string. – Lynn – 2015-12-21T00:47:32.333@Mauris, thank you, I'll add that – hargasinski – 2015-12-21T00:59:10.923