17
4
In this code golf, you will have to determine the direction of the shortest shot that hits exactly n cushions before falling into a pocket.
The billiard table is a 6 pocket pool table with the following characteristics:
- Dimensions are variable (a x b)
- No friction : the ball will roll forever until it falls into a pocket
- Pockets and ball sizes are almost zero. This means that the ball will fall in the pocket only if they have same position.
- The ball is placed at the bottom left hole at the beginning (but doesn't fall in it)
Create a full program or function that takes the dimensions (a,b) of the table and a the number of cushions to hit n as input and returns the angle in degrees of the shortest path hitting exactly n cushions before falling into a pocket.
- a > 0
- b > 0
- 0 <= n < 10000000
- 0 < alpha < 90 (in degrees) precision : at least 10^-6
examples :
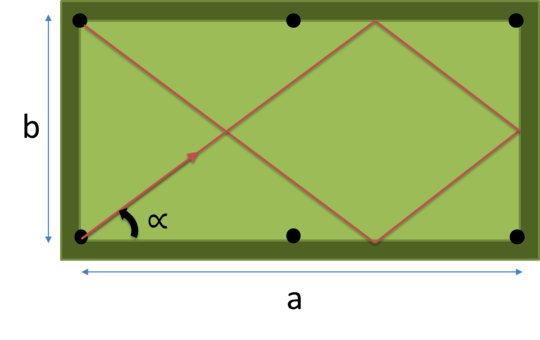
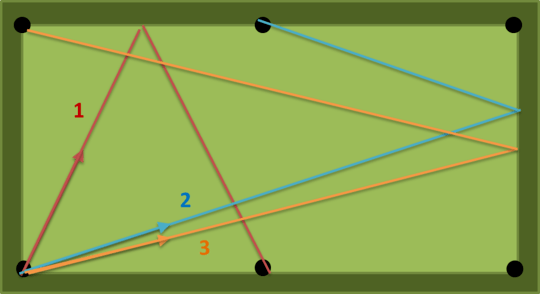
with a = 2, b = 1, n = 1 there are three possible paths : (1) (2) (3) on the following figure. the number (1) is the shortest so the output should be atan(2) = 63.43494882292201 degrees
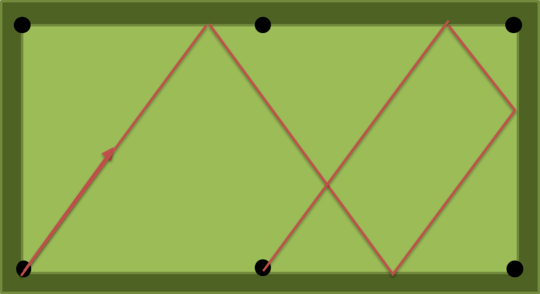
The solution for a = 2, b = 1, n = 4 is atan(4/3) = 53.13010235415598 degrees
test samples :
a = 2, b = 1, n = 1, -> alpha = 63.43494882292201
a = 2, b = 1, n = 2, -> alpha = 71.56505117707799
a = 2, b = 1, n = 3, -> alpha = 75.96375653207353
a = 2, b = 1, n = 4, -> alpha = 53.13010235415598
a = 2, b = 1, n = 5, -> alpha = 59.03624346792648
a = 2, b = 1, n = 6, -> alpha = 81.86989764584403
a = 4.76, b = 3.64, n = 27, -> alpha = 48.503531644784466
a = 2, b = 1, n = 6, -> alpha = 81.86989764584403
a = 8, b = 3, n = 33, -> alpha = 73.24425107080101
a = 43, b = 21, n = 10005, -> alpha = 63.97789961246943
This is code/billiard golf : shortest code wins!
Does the ball have to hit exactly
ncushions, or at leastncushions? – Peter Taylor – 2015-12-16T19:40:30.107@PeterTaylor exactly n cushions – Damien – 2015-12-16T19:41:01.490
isn´t the shortest path always back and forth between the left side top and bottom and then into one of the middle holes? – Eumel – 2015-12-17T08:55:21.673
no, look at the 2 1 4 example. This path is sqrt(25) = 5 long whereas your solution is sqrt(26) – Damien – 2015-12-17T09:49:21.560