40 Numbers in 9 Bytes

Question

There are 40 ways a directed Hamiltonian path can be arranged on a 3×3 grid:

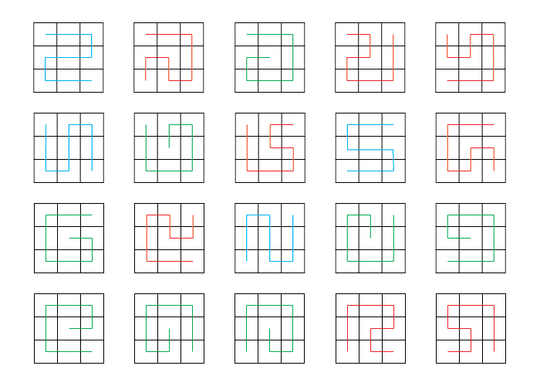
This graphic (thanks Sp3000!) shows only the 20 undirected paths. Traverse each colored line in both directions for the 40 directed paths.

Challenge

Using only printable ASCII, write a 3×3 grid of characters, such as:

ABC
DEF
GHI

When each of the 40 directed paths are read from this grid as 40 single-line, 9-character programs, the goal is to have each program output a unique integer from 1 to 40. Doing this for all 40 paths seems difficult and unlikely, so you only need to make it work for as many paths as you can.

The submission whose 40 path-programs output the most distinct numbers from 1 to 40 will be the winner. Tiebreaker goes to the earlier submission.

Path-programs that error or do not output an integer from 1 to 40 or output an integer that another path-program already covered are not counted. Specifically:

• Programs that error while compiling, running, or exiting are not counted. Warnings are ok.
• Programs that don't output an integer from 1 to 40 or output something slightly malformed such as -35 or 35 36 are not counted.
• Programs that require user input to produce the output are not counted.
• Programs that never end are not counted.
• From now on, programs that aren't deterministic aren't counted.
• Otherwise valid programs that output an integer from 1 to 40 that another valid program has already output are not counted. (The first program is counted.)
• Only programs that output integer representations of numbers from 1 to 40 (inclusive) are counted towards your total. The numbers are expected to be in the usual 1, 2, ..., 39, 40 format, unless that is not the norm for your language. (A trailing newline in the output is fine.)
• Which numbers your programs output and what order they are in does not matter. Only the number of distinct integers from valid programs matters.

All path-programs must be run in the same language. However, the "programs" may in fact be functions (with no required arguments) or REPL commands, as well as full programs, that print or return their target integer. You may mix and match between functions, REPL commands, and full programs.

Your 9 printable ASCII characters do not need to be distinct.

Example

If your 3×3 grid were

ABC
DEF
GHI

and your 40 programs and outputs looked like this

ABCFEDGHI -> 26
ABCFIHEDG -> 90
ABCFIHGDE -> 2
ABEDGHIFC -> syntax error
ADEBCFIHG -> prints 40 but then errors
ADGHEBCFI -> 6
ADGHIFCBE -> 6
ADGHIFEBC -> 6
CBADEFIHG -> runtime error
CBADGHEFI -> 3
CBADGHIFE -> 4
CFEBADGHI -> -32
CFIHEBADG -> 38.0
CFIHGDABE -> "36"
EDABCFIHG -> 33
EFCBADGHI -> no output
EHGDABCFI -> compilation error
EHIFCBADG -> 8
GDABCFEHI -> 22
GHEDABCFI -> 41
IHGDEFCBA -> 0
GDEHIFCBA -> '9'
EDGHIFCBA -> +10
CFIHGDEBA -> 11
GHIFCBEDA -> error
IFCBEHGDA -> error
EBCFIHGDA -> prints 23 but then loops infinitely
CBEFIHGDA -> randomly prints either 24 or 44
GHIFEDABC -> error
IFEHGDABC -> 30
EFIHGDABC -> 39
IHGDABEFC -> 7
GDABEHIFC -> 29
EBADGHIFC -> -1
GHIFCBADE -> 26
IHGDABCFE -> 1
IFCBADGHE -> error
GDABCFIHE -> no output
IHEFCBADG -> no output
IFCBADEHG -> "quack"

your score would be 14, because there are 14 distinct integers from 1 to 40 validly output, namely 26 2 6 3 4 33 8 22 11 30 39 7 29 1.

Answer 1

PARI/GP - 24

1%1
 8
2+3

PARI/GP ignores spaces between digits, so that 1 8 2, for example is treated as 182. The same could work for perl by replacing the spaces with underscores. I haven't exhausted the entire search space, so there may be better candidates.

A program can be fed to gp as gp -q -f program.gp, or interactively in the repl.

---

Output

1%1 8 2+3 -> 4
1%1 3+8 2 -> 83 # invalid
1%1 3+2 8 -> 29
1%8 2+3 1 -> 32
1 8%1 3+2 -> 7
1 2+8%1 3 -> 20
1 2+3 1%8 -> 19
1 2+3 8%1 -> 12
1%1 8 3+2 -> 3
1%1 2+8 3 -> 84 # invalid
1%1 2+3 8 -> 39
1 8%1 2+3 -> 9
1 3+8%1 2 -> 21
1 3+2 1%8 -> 18
8 1%1 3+2 -> 5
8 1%1 2+3 -> 12 # dup
8+2 1%1 3 -> 16
8+3 1%1 2 -> 15
2 1%1 8+3 -> 6
2+8 1%1 3 -> 5  # dup
3+2 8 1%1 -> 3  # dup
2 8+3 1%1 -> 28
8 2+3 1%1 -> 82 # invalid
1 3+2 8%1 -> 13
2+3 1%8 1 -> 33
3 1%8+2 1 -> 28 # dup
8%1 3+2 1 -> 29 # dup
1%8 3+2 1 -> 22
2+3 8 1%1 -> 2
3 8+2 1%1 -> 38
8 3+2 1%1 -> 83 # invalid
3+2 1%8 1 -> 24
2 1%8+3 1 -> 36
8%1 2+3 1 -> 39 # dup
2+3 1%1 8 -> 15 # dup
3+2 1%1 8 -> 6  # dup
3 1%1 2+8 -> 15 # dup
2 1%1 3+8 -> 16 # dup
3+8 1%1 2 -> 12 # dup
3 1%1 8+2 -> 15 # dup

All but 4 values are within the required range, with 12 duplicate entries.

---

Update

I've finished crunching, there are six distinct 23s, and only one 24 (as read by rows):

23 1%1 6 2+3 [2, 3, 4, 5, 7, 8, 11, 12, 13, 14, 16, 17, 18, 19, 22, 24, 26, 27, 32, 33, 34, 36, 37]
23 1 2%3+2*8 [2, 5, 7, 8, 10, 11, 12, 13, 14, 16, 17, 18, 19, 20, 22, 23, 25, 26, 29, 31, 32, 37, 40]
23 2 3%1+8 2 [2, 4, 6, 7, 10, 11, 12, 13, 14, 15, 16, 20, 21, 23, 24, 28, 29, 30, 31, 32, 33, 34, 40]
23 4%6%5*7+6 [2, 4, 5, 6, 7, 8, 9, 12, 13, 19, 21, 23, 24, 26, 29, 31, 32, 33, 34, 37, 38, 39, 40]
23 5%6%4*7+6 [2, 4, 5, 7, 8, 9, 10, 11, 12, 13, 14, 16, 18, 25, 26, 29, 31, 33, 34, 37, 38, 39, 40]
23 5%6%4*8+6 [1, 3, 5, 6, 8, 9, 10, 12, 14, 15, 18, 22, 24, 25, 27, 29, 30, 32, 34, 36, 37, 39, 40]

24 1%1 8 2+3 [2, 3, 4, 5, 6, 7, 9, 12, 13, 15, 16, 18, 19, 20, 21, 22, 24, 28, 29, 32, 33, 36, 38, 39]

The program I used for crunching is below. PARI/GP has limited string processing capabilities, so deal mainly with char arrays (a.k.a. Vecsmall). The operators tested are +, -, *, \ (floor div), %, ; (expression separator, essentially discards everything before it), and (space, as described above). The exponent operator ^ could also be added, but it becomes too slow to test exhaustively.

perms = {[
  [1, 2, 3, 6, 5, 4, 7, 8, 9], [1, 2, 3, 6, 9, 8, 5, 4, 7], [1, 2, 3, 6, 9, 8, 7, 4, 5], [1, 2, 5, 4, 7, 8, 9, 6, 3],
  [1, 4, 5, 2, 3, 6, 9, 8, 7], [1, 4, 7, 8, 5, 2, 3, 6, 9], [1, 4, 7, 8, 9, 6, 3, 2, 5], [1, 4, 7, 8, 9, 6, 5, 2, 3],
  [3, 2, 1, 4, 5, 6, 9, 8, 7], [3, 2, 1, 4, 7, 8, 5, 6, 9], [3, 2, 1, 4, 7, 8, 9, 6, 5], [3, 6, 5, 2, 1, 4, 7, 8, 9],
  [3, 6, 9, 8, 5, 2, 1, 4, 7], [3, 6, 9, 8, 7, 4, 1, 2, 5], [5, 4, 1, 2, 3, 6, 9, 8, 7], [5, 6, 3, 2, 1, 4, 7, 8, 9],
  [5, 8, 7, 4, 1, 2, 3, 6, 9], [5, 8, 9, 6, 3, 2, 1, 4, 7], [7, 4, 1, 2, 3, 6, 5, 8, 9], [7, 8, 5, 4, 1, 2, 3, 6, 9],
  [9, 8, 7, 4, 5, 6, 3, 2, 1], [7, 4, 5, 8, 9, 6, 3, 2, 1], [5, 4, 7, 8, 9, 6, 3, 2, 1], [3, 6, 9, 8, 7, 4, 5, 2, 1],
  [7, 8, 9, 6, 3, 2, 5, 4, 1], [9, 6, 3, 2, 5, 8, 7, 4, 1], [5, 2, 3, 6, 9, 8, 7, 4, 1], [3, 2, 5, 6, 9, 8, 7, 4, 1],
  [7, 8, 9, 6, 5, 4, 1, 2, 3], [9, 6, 5, 8, 7, 4, 1, 2, 3], [5, 6, 9, 8, 7, 4, 1, 2, 3], [9, 8, 7, 4, 1, 2, 5, 6, 3],
  [7, 4, 1, 2, 5, 8, 9, 6, 3], [5, 2, 1, 4, 7, 8, 9, 6, 3], [7, 8, 9, 6, 3, 2, 1, 4, 5], [9, 8, 7, 4, 1, 2, 3, 6, 5],
  [9, 6, 3, 2, 1, 4, 7, 8, 5], [7, 4, 1, 2, 3, 6, 9, 8, 5], [9, 8, 5, 6, 3, 2, 1, 4, 7], [9, 6, 3, 2, 1, 4, 5, 8, 7]
]}

ops = Vecsmall("+-*\\%; ")

ms = 1

for(c = 48, 57, {
 for(d = c, 57,
  for(f = d, 57,
   for(g = c, 57,
    for(e = 48, 57,
     print1(Strchr([c,d,e,f,g,13]));
     for(h = 1, #ops,
      for(i = 1, #ops,
       for(j = 1, #ops,
        for(k = 1, #ops,
         a = Vecsmall([c, ops[h], d, ops[i], e, ops[j], f, ops[k], g]);
         s = Set();
         for(m = 1, #perms,
          v = Strchr(vecextract(a, perms[m]));
          iferr(b = eval(v), E, b = 0);
          if(b >= 1 && b <= 40, s = setunion(s, [b]))
         );
         if(#s >= ms, ms = min(23, #s); print(#s, " ", Strchr(a), " ", s));
        )
       )
      )
     )
    )
   )
  )
 )
})

Answer 2

Deadfish, 18

This was actually the first language I tried before I considered infix operators. I'm posting it now for the sheer hilarity of the idea that Deadfish could be useful for something.

iii
ios
sii

For those who don't know Deadfish, i is increment, s is square and o is output, with the accumulator starting at 0 (there's also a 4th instruction d for decrement not used here). The fact that we don't have automatic printing and need to use o is a major drawback, but surprisingly Deadfish doesn't do too terribly here, all things considered. It turns out that the optimal placement of the output operator is in the middle.

iiisoisii 9
iiisiiois 11
iiisiisio 122
iioisiisi 2
iioiisiis 2
iisioiisi 5
iisiisiio 38
iisiisoii 36
iiiiosiis 4
iiiisiosi 17
iiiisiiso 324
isoiiisii 1
isiioiiis 3
isiisiiio 12
oiiiisiis 0
osiiiisii 0
oisiiiisi 0
oiisiiiis 0
siiiisoii 16
sioiiiisi 1
iisiosiii 5
sioiisiii 1
oisiisiii 0
isiisioii 10
siisiioii 6
isiioisii 3
oiisiisii 0
iiosiisii 2
siisoiiii 4
isoisiiii 1
osiisiiii 0
iisiiiosi 7
siiioiisi 3
oiiisiisi 0
siisiiiio 8
iisiiiiso 64
isiiiisio 26
siiiisiio 18
iiosiiiis 2
isiiiiois 5

Answer 3

Python REPL and many more, 22 23

6+7
*5%
6%4

Key observation: If you colour the grid like a checkerboard, the path alternates grid colours as it goes and starts and ends on the same colour.

Still brute forcing for better. Trying with +*% (and even ** for languages where ^ is exponentiation) didn't turn up anything better, unfortunately. I also tried throwing in bitwise operators and only ^ (xor) seemed to mildly help, but the search was taking too long so I've given up.

6+7%5*6%4 6
6+7%4%5*6 24
6+7%4%6*5 21
6+5*6%4%7 8
6*5+7%4%6 33
6*6%5+7%4 4
6*6%4%7+5 5
6*6%4%5+7 7
7+6*5%4%6 9
7+6*6%5%4 8
7+6*6%4%5 7
7%5+6*6%4 2
7%4%5+6*6 39
7%4%6*6+5 23
5*6+7%4%6 33
5%7+6*6%4 5
5%6*6+7%4 33
5%4%7+6*6 37
6*6+7%5%4 38
6%5*6+7%4 9
4%6*5%7+6 12
6*5%4%7+6 8
5*6%4%7+6 8
7%4%6*5+6 21
6%4%7+5*6 32
4%7+5%6*6 34
5+7%4%6*6 23
7+5%4%6*6 13
6%4%5*6+7 19
4%5%6*6+7 31
5%4%6*6+7 13
4%6*6+5%7 29
6*6+5%4%7 37
5+6*6%4%7 5
6%4%7+6*5 32
4%6*6+7%5 26
4%7+6*6%5 5
6*6+7%4%5 39
4%5%7+6*6 40
4%7+6*5%6 4

Answer 4

J, 15

2 + 1
* 3 *
2 + 3

This outputs only valid numbers, but a lot are duplicates. The unique values are 17 11 16 28 31 23 13 10 21 33 18 24 22 29 27. You can definitely do better by changing operators and the integers involved.

2+1*3*2+3 -> 17
2+1*3+3*2 -> 11
2+1*3+2*3 -> 11
2+3*2+3*1 -> 17
2*3+1*3+2 -> 16
2*2+3+1*3 -> 16
2*2+3*1+3 -> 28
2*2+3*3+1 -> 28
1+2*3*3+2 -> 31
1+2*2+3*3 -> 23
1+2*2+3*3 -> 23
1*3+2*2+3 -> 13
1*3+3+2*2 -> 10
1*3+2*2+3 -> 13
3*2+1*3+2 -> 21
3*1+2*2+3 -> 33
3+2*2+1*3 -> 13
3+3*1+2*2 -> 18
2*2+1*3+3 -> 16
2+3*2+1*3 -> 17
3+2*3*1+2 -> 21
2*3+3*1+2 -> 24
3*2+3*1+2 -> 33
1*3+2*3+2 -> 13
2+3*1+3*2 -> 23
3*1+3+2*2 -> 24
3+1*3+2*2 -> 10
1+3*3+2*2 -> 22
2+3*3*2+1 -> 29
3*3+2*2+1 -> 27
3*3+2*2+1 -> 27
3+2*2+3*1 -> 13
2*2+3+3*1 -> 16
3+2*2+3*1 -> 13
2+3*1+2*3 -> 23
3+2*2+1*3 -> 13
3*1+2*2+3 -> 33
2*2+1*3+3 -> 16
3+3*1+2*2 -> 18
3*1+2*3+2 -> 33

Answer 5

><>, 36*

If you're lucky enough!

x;x
lxl
xnx

Since the challenge does not require the code to be deterministic we only have to prove that it is possible (even if improbable) to return 36 numbers and we are done. It was good while it lasted I guess.

(For those not familiar with ><>, a great intro on can be found here)

><> is a stack-based 2D language. This means that instructions aren't executed linearly like most traditional languages — program flow can be up, down, left or right!

I decided to use the "x" instruction in ><>, which changes the instruction pointers direction to either up, down, left or right at random. Since our code will only be one line, that means that we can only look at the cases when it goes right or left, since if the pointer goes up or down, it will just hit the "x" instruction again.

The "n" instruction pops the number at the top of the stack and prints it. However if the stack is empty and there is nothing to pop, an error is raised.

The "l" instruction simply pushes the length of the stack onto the stack (and lucky for us it does not send an error if the stack is empty), so for example if the stack were empty and "l" would be called, it would push 0 onto the stack. If we would now again call "l", then since the stack has one element (0), it would push 1 to the top of the stack and now that would mean that there would be two things on the stack and that would mean that if we were to call "l" again, we would push 2 onto the stack etc. So we can use "l" to push an arbitrary number onto the stack via the method shown earlier.

The ";" instruction ends the program.

The idea with using "x" is that, for example if there was only one "x" in the code (where A,B,C,D are some instructions):

ABCx;D

The program would execute A then B then C, and upon reaching "x" we would have two possibilites: the code either continues to go right and hits the ";" and exits or it goes left and executes C then B then A then D and only then exits. So if our code contained one "x", the program gains two possible program flows from which we may choose the most suited program.

I there are two or more "x"es then we gain an infinite number of possible program flows.

Our code has five "x"es, futhermore each of them is in a "starting cell" of the Hamiltonian paths, which means every single program will start with an "x", and every program will have the structure:

xAxBxCxDx

Where A, B, C, D belong to { ; , n, l, l} This means that there are only 12 unique programs. Furthermore since we always start on an "x", we may look at the case when the program goes left, thus symmetric programs can also be regarded the same. Up to symmetry there are only 6 different posible programs. Only 4 of them occur in the programs generated as hamiltonian paths:

xnxlxlx;x
xlxnxlx;x
xnxlx;xlx
xlxnx;xlx

Let us look at the first program "xnxlxlx;x" if we go right at the first step we hit the print command which will raise an error since we have nothing on the stack. If we go left we hit the end program command. So we cannot output any number from these programs.

The second program, "xlxnxlx;x", is a lot more hopeful, since upon going right at the begining a zero is put on the stack, if we then go left at the next "x", our stack gains a one, then going right again we have a 2 that we can then print and continue going right to end the program. We can observe that we can actually print any even number, since in the "xlx" part at the beginning we can reach a number of arbitrary size by going right then left then right again a certain number of times.

Similiarly it can be seen that the third program xnxlx;xlx can output any odd number, by going left at the beginning and then repeating the "xlx" routine only this time going left then right then left.

And the fourth program is essentially the same as the second program and can output any even number.

So for the required programs we have:

x;xlxlxnx (none)
x;xlxnxlx (any even number)
x;xlxnxlx (any even number)
x;xlxnxlx (any even number)
xlx;xlxnx (any odd number)
xlxnx;xlx (any even number)
xlxnxlx;x (any even number)
xlxnxlx;x (any even number)
x;xlxlxnx (none)
x;xlxnxlx (any even number)
x;xlxnxlx (any even number)
xlx;xlxnx (any odd number)
xlxnx;xlx (any even number)
xlxnxlx;x (any even number)
xlx;xlxnx (any odd number)
xlx;xlxnx (any odd number)
xnxlx;xlx (any odd number)
xnxlx;xlx (any odd number)
xlx;xlxnx (any odd number)
xnxlx;xlx (any odd number)
xnxlxlx;x (none)
xlxnxlx;x (any even number)
xlxnxlx;x (any even number)
xlxnxlx;x (any even number)
xnxlx;xlx (any odd number)
xlx;xnxlx (any even number)
x;xlxnxlx (any even number)
x;xlxnxlx (any even number)
xnxlxlx;x (none)
xlxnxlx;x (any even number)
xlxnxlx;x (any even number)
xnxlx;xlx (any odd number)
xlx;xnxlx (any even number)
x;xlxnxlx (any even number)
xnxlx;xlx (any odd number)
xnxlx;xlx (any odd number)
xlx;xlxnx (any odd number)
xlx;xlxnx (any odd number)
xnxlx;xlx (any odd number)
xlx;xlxnx (any odd number)

That's 4 programs that cant output numbers, 20 that can output any even number, 16 that can output any odd number. Since there are exactly 20 even numbers and at least 16 odd numbers in the range 1 to 40, then with a certain probability there exists a possibility that there would be 36 different numbers in the range 1 to 40 output by this code block.

Answer 6

GolfScript, 8

192
6#7
281

Currently the highest scoring solution. :P Was nice while it lasted.

Programs

1927#6281 1927
192718#62 192718
19271826# 19271826
19#628172 19
16#927182 16
1628#9271 1628
16281729# 16281729
162817#92 162817
2916#7182 2916
291628#71 291628
29162817# 29162817
27#916281 27
2718#9162 2718
27182619# 27182619
#61927182 
#72916281 
#82619271 
#81729162 
261927#81 261927
28#619271 28
1826#7291 1826
26#817291 26
#62817291 
271826#91 271826
281729#61 281729
1729#8261 1729
#92718261 
29#718261 29
2817#6192 2817
17#826192 17
#71826192 
182619#72 182619
2619#8172 2619
#91628172 
28172916# 28172916
18261927# 18261927
17291628# 17291628
26192718# 26192718
18#729162 18
172916#82 172916

Answer 7

CJam, 14

3(4
;];
0)1

Below the working programs:

3(4;];0)1 = 11
3(4;1)0;] = 22
3(];0)1;4 = 14
3;0)](4;1 = 11
3;0)1;4(] = 13
3;0)1;](4 = 14
4(3;];1)0 = 20
4(3;0)];1 = 1
4(3;0)1;] = 31
4;1)](3;0 = 20
4;1)0;3(] = 22
0;3(4;])1 = 21
0)];3(4;1 = 21
1)0;];4(3 = 33
4;1)0;](3 = 23
0)1;4(];3 = 3
1;4(])0;3 = 33
4(];1)0;3 = 23
0)1;];3(4 = 24
1)0;3(];4 = 4
0;3(])1;4 = 24
0)1;4(3;] = 13
1)0;3(4;] = 22
1;4(3;0)] = 31
0;3(4;1)] = 22
1)];4(3;0 = 30
1;4(3;])0 = 30

The values generated are: [1, 3, 4, 11, 13, 14, 20, 21, 22, 23, 24, 30, 31, 33]

Answer 8

dc (20)

2+3
*p+
4+5

ABCFEDGHI -> 2+3+p*4+5 -> 5     $ **
ABCFIHEDG -> 2+3+5+p*4 -> 10    $ **
ABCFIHGDE -> 2+3+5+4*p -> 40    $ **
ABEDGHIFC -> 2+p*4+5+3 -> 2     $ **
ADEBCFIHG -> 2*p+3+5+4 -> 2       **
ADGHEBCFI -> 2*4+p+3+5 -> 6     $ **
ADGHIFCBE -> 2*4+5+3+p -> 14    $ **
ADGHIFEBC -> 2*4+5+p+3 -> 11    $ **
CBADEFIHG -> 3+2*p+5+4 -> 6       **
CBADGHEFI -> 3+2*4+p+5 -> 10      **
CBADGHIFE -> 3+2*4+5+p -> 15    $ **
CFEBADGHI -> 3+p+2*4+5 -> 3     $ **
CFIHEBADG -> 3+5+p+2*4 -> 8     $ **
CFIHGDABE -> 3+5+4*2+p -> 34    $ **
EDABCFIHG -> p*2+3+5+4 -> 
EFCBADGHI -> p+3+2*4+5 -> 
EHGDABCFI -> p+4*2+3+5 -> 
EHIFCBADG -> p+5+3+2*4 -> 
GDABCFEHI -> 4*2+3+p+5 -> 9     $ **
GHEDABCFI -> 4+p*2+3+5 -> 4     $ **
IHGDEFCBA -> 5+4*p+3+2 -> 20    $ **
GDEHIFCBA -> 4*p+5+3+2 -> 4       **
EDGHIFCBA -> p*4+5+3+2 -> 
CFIHGDEBA -> 3+5+4*p+2 -> 32    $ **
GHIFCBEDA -> 4+5+3+p*2 -> 12    $ **
IFCBEHGDA -> 5+3+p+4*2 -> 8       **
EBCFIHGDA -> p+3+5+4*2 -> 
CBEFIHGDA -> 3+p+5+4*2 -> 3       **
GHIFEDABC -> 4+5+p*2+3 -> 9       **
IFEHGDABC -> 5+p+4*2+3 -> 5       **
EFIHGDABC -> p+5+4*2+3 -> 
IHGDABEFC -> 5+4*2+p+3 -> 22    $ **
GDABEHIFC -> 4*2+p+5+3 -> 6       **
EBADGHIFC -> p+2*4+5+3 -> 
GHIFCBADE -> 4+5+3+2*p -> 24    $ **
IHGDABCFE -> 5+4*2+3+p -> 25    $ **
IFCBADGHE -> 5+3+2*4+p -> 20      **
GDABCFIHE -> 4*2+3+5+p -> 14      **
IHEFCBADG -> 5+p+3+2*4 -> 5       **
IFCBADEHG -> 5+3+2*p+4 -> 16    $ **

32 outputs, 20 of them distinct (marked with a $)

2, 3, 4, 5, 6, 8, 9, 10, 11, 12, 14, 15, 16, 20, 22, 24, 25, 32, 34, 40