14
0
This is code golf. The winner is the valid code with the smallest number of bytes.
Challenge
Given inputs M and N, the width and height of a rectangular grid of squares, output a polygon that satisfies the following:
- The polygon edges are made up only of square edges: there are no diagonal edges - all are vertical or horizontal.
- The polygon has no holes: every square outside the polygon may be reached by orthogonal steps on squares outside the polygon, starting from a square outside the polygon on the outer boundary of the rectangle.
- The polygon has no self-intersection: of the square edges meeting at a vertex, no more than 2 may be part of the polygon perimeter.
- The polygon is connected: any square in the polygon must be reachable from any other square in the polygon via orthogonal steps that stay within the polygon.
- The polygon has the maximum possible perimeter: according to the formula shown below.
Your code must work for M and N from 1 to 255.
Formula for maximum perimeter
The challenge here is finding the most golfable of those polygons with the maximum perimeter. The maximum perimeter itself is always defined by the formula:
This is true because for a maximum perimeter every square vertex must be on the perimeter. For an odd number of vertices this is not possible and the best that can be attained is one vertex less (since the perimeter is always even).
Output
Output the shape as a string of newline separated characters (N rows of exactly M characters). Here I am using space for squares outside the polygon, and '#' for squares inside the polygon, but you may use any two visually distinct characters, provided their meaning is consistent for all inputs.
You may include up to one leading newline and up to one trailing newline.
If you wish, you may instead output M rows of exactly N characters, and you may choose M by N output for some inputs and N by M output for others.
Examples
Invalid due to a hole:
###
# #
###
Invalid due to intersection (touching diagonally - a vertex with 4 square edges on the perimeter) and, incidentally, a hole:
##
# #
###
Invalid due to being disconnected:
#
# #
#
Valid polygon of maximum perimeter:
# #
# #
###
Credits
I initially underestimated how quickly the value of the maximum perimeter could be calculated, and was going to just ask for that value as the output. Thanks to the wonderfully helpful people in chat for explaining how to work out the maximum perimeter for arbitrary N and M and helping turn this into a challenge that will last for more than one answer...
Specifically thanks to:
Sparr, Zgarb, feersum, jimmy23013.
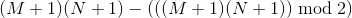
I could name this question using polyominos or polygons (since both apply). Does anyone have a preference? You can indicate with comment voting on the following: – trichoplax – 2015-06-25T17:50:53.270
5Highest perimeter polyomino – trichoplax – 2015-06-25T17:51:13.210
1Highest perimeter connected polygon – trichoplax – 2015-06-25T17:51:22.000
N rows of exactly M characters: can we interchange the two input values if we find it convenient for certain inputs? – Level River St – 2015-06-25T18:11:58.173
@steveverrill Both inputs are from 1 to 255. I can't see a benefit to switching their order. Do you mean outputting in a different order, or something else I'm missing? – trichoplax – 2015-06-25T18:16:08.707
(even if there's a benefit I'm inclined to insist on the output being aligned as specified, but I'll delay making the decision until I'm sure I haven't misunderstood something) – trichoplax – 2015-06-25T18:17:37.323
For example, if you have a particular strategy for shapes with one side even and one side odd, you might prefer to draw an odd number of lines with an even number of characters. That would be great if M was even and N was odd. But if the user decides to give the odd number first then the even number, can we switch them round? – Level River St – 2015-06-25T18:22:16.270
@steveverrill that makes perfect sense now - thank you. I'll leave it as is for now while I think about it, as it's easier to make that change forwards than backwards, and I'll let you know what I decide after a think. – trichoplax – 2015-06-25T18:26:50.750
3@steveverrill I've edited the Output section. Does that fit your request? – trichoplax – 2015-06-25T18:38:19.060
That suits me fine! First upvote on your last comment is not mine, so I guess it suits someone else, too. – Level River St – 2015-06-25T19:12:12.903
That change in the output rules should make it simpler. Of course it was your choice if you wanted to make it easier. BTW, I believe I know how to solve this cleanly. So in the likely case that somebody else posts the same kind of solution first before I get to work on it tonight: I did not steal their idea! :) – Reto Koradi – 2015-06-25T19:49:20.717
@RetoKoradi yes I'm happy making it slightly easier in order to see a different approach – trichoplax – 2015-06-25T19:56:22.667
@RetoKoradi I only see it as making the output easier, which isn't the point of the challenge, so I'm happy with it – trichoplax – 2015-06-25T19:57:28.337
I think this will be all about generating the output with the shortest possible code. The pattern that needs to be generated looks fairly straightforward. As I expected, @steverrill already implemented exactly the pattern I also had in mind. – Reto Koradi – 2015-06-25T20:55:15.297
@RetoKoradi yes that's what I expected. Unless some languages find different patterns more suitable for golfing most people will probably choose similar patterns. – trichoplax – 2015-06-25T20:57:45.687