Constructing an Orthogonal-Diagonal Greco-Latin Square

Question

Consider a grid of NxN unique elements. Each element has a letter (from A to the Nth letter, inclusive) and a number (from 1 to N, inclusive). Hence, each number/letter pair is in the grid exactly once.

Your job is to arrange a grid such that:

Each row, column, and diagonal (including wrapping) contains each letter and number exactly once.

By wrapping, I mean that

* * * # *
* * # * * 
* # * * *
# * * * *
* * * * #

is a diagonal, along with all similar diagonals that hit the edges.

An example 5x5 grid is:

A1 B2 C3 D4 E5
C4 D5 E1 A2 B3
E2 A3 B4 C5 D1
B5 C1 D2 E3 A4
D3 E4 A5 B1 C2

Your task is to write a program that accepts a number, N, and print a NxN grid as described above. Your program should work for any 0 < N <= 26. If a particular grid is not possible, then you should print Impossible.

Hardcoding the answer for any N is not allowed. A program is hard coded if it calculates the grid in different manner (as judged by me) for any N > 26 (or if it fails to calculate). (This is meant to prevent precalculation, including precalculated invalid grids, or offsets for given grids).

This is a fastest-code problem, and your score is the sum of the times taken to run your program across all possible N on my computer. In your answer, please have your program run across all N (so I only have to time it once). If no program can compute it in under 60 seconds, then the winner is the answer that can calculate the grid with the largest N in 60 seconds. If multiple programs have the same maximum N, then the tiebreaker is the fastest solution.

(I have a decently powered Windows 8 machine, and any compilers or interpreters needed must be freely available for it).

Answer 1

Python 3

letters = []
numbers = []
for n in range(1,27): 
    if n%2==0 or n%3==0:
        offsets=False
    else:
        offsets = [x for x in range(0,n,2)]
        offsets.extend([x for x in range(1,n,2)])
    letters.append(chr(96+n))
    numbers.append(n)
    if offsets :
        for y in range(n):
            for x in range(n):
                let=letters[(x+offsets[y])%n]
                num=numbers[(offsets[y]-x)%n]
                print (let+str(num), end= "  " if num<10 else " ")
            print("\n")     
    else: 
        print("Impossible\n")

How it works?

The naive implementation would be to look through all the possible arrangements of letter and numbers in an NxN grid and look for one that is also a Orthogonal-Diagonal Latin Square (ODLS) (and thus, for some it would just have to go through all configurations and return impossible). Such an algorithm wouldnt suit this challenge due to absurd time complexity. So there are three major simplifications and justifications (partial proofs and insights to why it works) to ODLS constructions used in my implementation:

The first is the notion that we only need to generate a valid Diagonal Latin Square (A NxN grid such that each row, column, wrapped-diagonal contains each element of a set of N distinct elements exactly once) of the first N letters of the alphabet. If we can construct such a Diagonal Latin Square (DLS) then an ODLS can be constructed using the DLS with appropriate exchange of elements and flipping. Justification:

Let us first look at an example using the example grid
a1 b2 c3 d4 e5
c4 d5 e1 a2 b3
e2 a3 b4 c5 d1
b5 c1 d2 e3 a4
d3 e4 a5 b1 c2
Every ODLS can be separated into two DLS (by definition), so
we can separate the grid above into two DLS, one containing letters, the other - numbers
a b c d e
c d e a b
e a b c d
b c d e a
d e a b c
and
1 2 3 4 5 
4 5 1 2 3
2 3 4 5 1
5 1 2 3 4 
3 4 5 1 2
If we transform the number DLS by the mapping 1-->e, 2-->d, 3-->c, 4-->b, 5-->a,
1 2 3 4 5 --> e d c b a
4 5 1 2 3 --> b a e d c
2 3 4 5 1 --> d c b a e
5 1 2 3 4 --> a e d c b
3 4 5 1 2 --> c b a e d
Now if we put the transformed number grid next to the original letter grid,
Original  | Transformed
a b c d e | e d c b a
c d e a b | b a e d c
e a b c d | d c b a e
b c d e a | a e d c b
d e a b c | c b a e d
It can be clearly seen that the number grid is a horizontal flip of
the letter grid withminor letter to number substitutions.
Now this works because flipping guarantees that no two pairs occur more than once,
and each DLS  satisfies the requirements of the ODLS.

The second simplification is the notion that if we found a suitable configuration (SC) of one element (A NxN grid such that each row, column, wrapped-diagonal contains that element exactly once), then a DLS could be constructed by replacing the element and shifting the SC. Justification:

If "_" is an empty space and "a" the element then a valid SC of a 7x7 grid is
a _ _ _ _ _ _
_ _ a _ _ _ _
_ _ _ _ a _ _
_ _ _ _ _ _ a
_ a _ _ _ _ _ 
_ _ _ a _ _ _
_ _ _ _ _ a _
or
a _ _ _ _ _ _
_ _ _ a _ _ _
_ _ _ _ _ _ a
_ _ a _ _ _ _
_ _ _ _ _ a _ 
_ a _ _ _ _ _
_ _ _ _ a _ _
(the second one can actually be obtained from the first one via rotation)
now say we took the second SC, shifted it one unit to the right and 
replaced all "a" with "b"
a _ _ _ _ _ _       _ a _ _ _ _ _       _ b _ _ _ _ _
_ _ _ a _ _ _       _ _ _ _ a _ _       _ _ _ _ b _ _
_ _ _ _ _ _ a       a _ _ _ _ _ _       b _ _ _ _ _ _
_ _ a _ _ _ _  -->  _ _ _ a _ _ _  -->  _ _ _ b _ _ _
_ _ _ _ _ a _       _ _ _ _ _ _ a       _ _ _ _ _ _ b
_ a _ _ _ _ _       _ _ a _ _ _ _       _ _ b _ _ _ _
_ _ _ _ a _ _       _ _ _ _ _ a _       _ _ _ _ _ b _
Now if we overlaid the SC of "a" with the SC of "b" we get
a b _ _ _ _ _
_ _ _ a b _ _
b _ _ _ _ _ a
_ _ a b _ _ _
_ _ _ _ _ a b 
_ a b _ _ _ _
_ _ _ _ a b _
If we repeated these steps for the other five letters, we would arrive at a DLS
a b c d e f g
e f g a b c d
b c d e f g a
f g a b c d e
c d e f g a b 
g a b c d e f
d e f g a b c
This is a DLS, since each SC follows the general requirements of a DLS 
and shifting ensured that each element has its own cell.
Another thing to note is that each row contains the string "abcdefg" that is offset 
by some cells. This leads to another simplification: we only need to find the 
offsets of the string in every row and we are finished.

The last simplification is as follows - all DLS of prime N, except for N=2 or N=3, can be constructed, and if N can be factored into two numbers whose appropriate DLS can be constructed, then a DLS of that N can be constructed. I conjecture that the converse also holds. (In other words we can only construct an DLS for N that is not divisible by 2 or 3)

Pretty obvious why 2x2 or 3x3 cant be made. For any other prime this can be done
by assigning a each consecutive row a shift that is by two bigger than the previous, 
for N=5 and N=7 this looks like (with elements other than "a" ommited)
N=5
a _ _ _ _ offset = 0
_ _ a _ _ offset = 2
_ _ _ _ a offset = 4
_ a _ _ _ offset = 6 = 1 (mod 5)
_ _ _ a _ offset = 8 = 3 (mod 5)
N=7
a _ _ _ _ _ _ offset = 0
_ _ a _ _ _ _ offset = 2
_ _ _ _ a _ _ offset = 4
_ _ _ _ _ _ a offset = 6
_ a _ _ _ _ _ offset = 8 = 1 (mod 7)
_ _ _ a _ _ _ offset = 10 = 3 (mod 7)
_ _ _ _ _ a _ offset = 12 = 5 (mod 7
(Why this works on all prime N (actually all N that are not divisible
by 3 or 2) can probably be proven via some kind of induction but i will
omit that, this is just what my code uses and it works)
Now, the first composite number that is not
divisible by 2 or 3 is 25 (it also occurs in the range our program must test)
Let A denote the DLS of N = 5
a b c d e 
d e a b c 
b c d e a 
e a b c d 
c d e a b
Let F be the DLS A where each letter is substituted by the letter five postions after it 
a-->f, b-->g etc. So F is 
f g h i j 
j e f g h 
g h i j f 
j f g h i 
h i j f g
Let K be the DLS a where each letter is substituted by the letter ten postions after it
a-->k, b--> l etc.
Let P be defined likewise (so a-->p, b-->q etc)
Let U be defined likewise (so a-->u, b-->v etc)
Now, since the DLS A could be constructed, then by substituting a --> A, b--> F etc.
we get a DLS of N=5*5 (A has five rows and five columns and each is filled with a 
grid of five rows and five columns)
A F K P U
P U A F K
F K P U A
U A F K P
K P U A F
Now since smaller DLS in the big DLS satisfies the 
conditions of a DLS and the big one also satisfies the DLS conditions,
then the resulting grid is also a DLS 

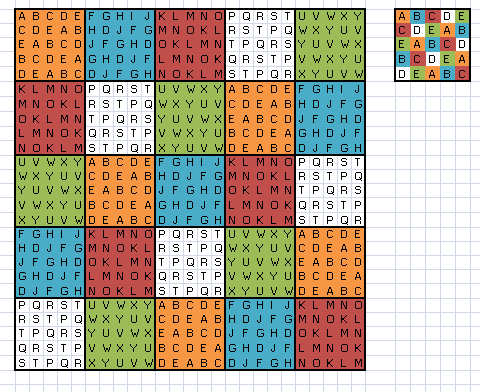
A picture of what i meant with the smaller - bigger DLS

Now this kind of thing works for all constructible N and can be proven similiarly.

I have a strong sense that the converse (if some N isnt constructible
(2 and 3) then no multiple of that N is constructible) is also true but have a hard time 
proving it (test data up to N=30 (took a veeery long time to calculate) confirm it though)