48
7
Single moves
The board is an infinite 2 dimensional square grid, like a limitless chess board. A piece with value N (an N-mover) can move to any square that is a distance of exactly the square root of N from its current square (Euclidean distance measured centre to centre).
For example:
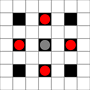
- A 1-mover can move to any square that is horizontally or vertically adjacent
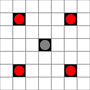
- A 2-mover can move to any square that is diagonally adjacent
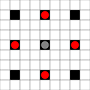
- A 5-mover moves like a chess knight
Note that not all N-movers can move. A 3-mover can never leave its current square because none of the squares on the board are a distance of exactly root 3 from the current square.
Multiple moves
If allowed to move repeatedly, some pieces can reach any square on the board. For example, a 1-mover and a 5-mover can both do this. A 2-mover can only move diagonally and can only reach half of the squares. A piece that cannot move, like a 3-mover, cannot reach any of the squares (the starting square is not counted as "reached" if no movement occurs).
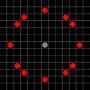
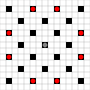
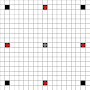
The images show which squares can be reached. More details on hover. Click for larger image.
- Squares reachable in 1 or more moves are marked in black
- Squares reachable in exactly 1 move are shown by red pieces
(apart from the 3-mover, which cannot move)
What proportion of the board can a given N-mover reach?
Input
- A positive integer N
Output
- The proportion of the board that an N-mover can reach
- This is a number from 0 to 1 (both inclusive)
- For this challenge, output as a fraction in lowest terms, like 1/4, is allowed
So for input 10, both 1/2 and 0.5 are acceptable outputs. Output as separate numerator and denominator is also acceptable, to be inclusive of languages that support neither floats nor fractions. For example, 1 2 or [1, 2].
For the integer outputs (0 and 1), any of the following are acceptable formats:
- For 0:
0,0.0,0/1,0 1,[0, 1] - for 1:
1,1.0,1/1,1 1,[1, 1]
Scoring
This is code golf. The score is the length of the code in bytes. For each language, the shortest code wins.
Test cases
In the format input : output as fraction : output as decimal
1 : 1 : 1
2 : 1/2 : 0.5
3 : 0 : 0
4 : 1/4 : 0.25
5 : 1 : 1
6 : 0 : 0
7 : 0 : 0
8 : 1/8 : 0.125
9 : 1/9 : 0.1111111111111111111111111111
10 : 1/2 : 0.5
13 : 1 : 1
16 : 1/16 : 0.0625
18 : 1/18 : 0.05555555555555555555555555556
20 : 1/4 : 0.25
25 : 1 : 1
26 : 1/2 : 0.5
64 : 1/64 : 0.015625
65 : 1 : 1
72 : 1/72 : 0.01388888888888888888888888889
73 : 1 : 1
74 : 1/2 : 0.5
80 : 1/16 : 0.0625
81 : 1/81 : 0.01234567901234567901234567901
82 : 1/2 : 0.5
144 : 1/144 : 0.006944444444444444444444444444
145 : 1 : 1
146 : 1/2 : 0.5
148 : 1/4 : 0.25
153 : 1/9 : 0.1111111111111111111111111111
160 : 1/32 : 0.03125
161 : 0 : 0
162 : 1/162 : 0.006172839506172839506172839506
163 : 0 : 0
164 : 1/4 : 0.25
241 : 1 : 1
242 : 1/242 : 0.004132231404958677685950413223
244 : 1/4 : 0.25
245 : 1/49 : 0.02040816326530612244897959184
260 : 1/4 : 0.25
261 : 1/9 : 0.1111111111111111111111111111
288 : 1/288 : 0.003472222222222222222222222222
290 : 1/2 : 0.5
292 : 1/4 : 0.25
293 : 1 : 1
324 : 1/324 : 0.003086419753086419753086419753
325 : 1 : 1
326 : 0 : 0
360 : 1/72 : 0.01388888888888888888888888889
361 : 1/361 : 0.002770083102493074792243767313
362 : 1/2 : 0.5
369 : 1/9 : 0.1111111111111111111111111111
370 : 1/2 : 0.5
449 : 1 : 1
450 : 1/18 : 0.05555555555555555555555555556
488 : 1/8 : 0.125
489 : 0 : 0
490 : 1/98 : 0.01020408163265306122448979592
520 : 1/8 : 0.125
521 : 1 : 1
522 : 1/18 : 0.05555555555555555555555555556
544 : 1/32 : 0.03125
548 : 1/4 : 0.25
549 : 1/9 : 0.1111111111111111111111111111
584 : 1/8 : 0.125
585 : 1/9 : 0.1111111111111111111111111111
586 : 1/2 : 0.5
592 : 1/16 : 0.0625
593 : 1 : 1
596 : 1/4 : 0.25
605 : 1/121 : 0.008264462809917355371900826446
610 : 1/2 : 0.5
611 : 0 : 0
612 : 1/36 : 0.02777777777777777777777777778
613 : 1 : 1
624 : 0 : 0
625 : 1 : 1








10
I posted this question on Math.SE: https://math.stackexchange.com/questions/3108324/how-much-of-an-infinite-board-can-a-n-mover-reach
– infmagic2047 – 2019-02-11T04:27:37.913Interesting conjecture! – trichoplax – 2019-02-11T10:06:31.180
1"A piece that cannot move, like a 3-mover, cannot reach any of the squares". Interestingly enough, even if you count the starting square, since the board is infinite, it still converges to 0 as a proportion. – Beefster – 2019-02-11T17:10:57.773
@Beefster good point. I went with this way to make the limit easier to find without having to go all the way to infinity... – trichoplax – 2019-02-11T18:13:57.240
I like how you used the description of the images properly, now I can just hover my mouse over the images to see what image is what kind of a mover – Ferrybig – 2019-02-12T09:55:18.593
@Ferrybig the image description is used by screen readers, but the text you see when you hover is different - if you edit the question you'll see the hover text in quotes at the very end of the plain text. Ideally everyone would specify both. Glad you found it useful :) – trichoplax – 2019-02-12T13:01:04.203
2
@infmagic2047 's math.se question about the prime factoring approach now has an answer with a complete proof.
– Ørjan Johansen – 2019-02-13T18:10:43.680@trichoplax What does "lowest terms" mean when applied to zero? Would it be acceptable to return a result of zero as
[0, 107],[0, 43],[0, 12], etc., or does it always have to be in the form of[0, 1]? – Deadcode – 2019-02-26T04:57:26.763I've edited to clarify lowest terms for outputs 0 and 1. – trichoplax – 2019-02-26T20:38:13.490