Plight of the Concorde

Question

Background

The traveling salesman problem (TSP) asks for the shortest circuit that visits a given collection of cities. For the purposes of this question, the cities will be points in the plane and the distances between them will be the usual Euclidean distances (rounded to the nearest integer). The circuit must be "round-trip", meaning it must return to the starting city.

The Concorde TSP solver can solve instances of the Euclidean traveling salesman problem, exactly and much faster than one would expect. For example, Concorde was able to solve an 85,900-point instance exactly, parts of which look like this:

However, some TSP instances take too long, even for Concorde. For example, no one has been able to solve this 100,000-point instance based on the Mona Lisa. (There is a $1,000 prize offered if you can solve it!)

Concorde is available for download as source code or an executable. By default, it uses the built-in linear program (LP) solver QSopt, but it can also use better LP solvers like CPLEX.

The challenge

What is the smallest TSP instance you can generate that takes Concorde more than five minutes to solve?

You can write a program to output the instance, or use any other method you would like.

Scoring

The fewer points in the instance the better. Ties will be broken by the file size of the instance (see below).

Standardization

Different computers run faster or slower, so we will use the NEOS Server for Concorde as the standard of measurement for runtime. You can submit a list of points in the following simple 2-d coordinate form:

#cities
x_0 y_0
x_1 y_1
.
.
.
x_n-1 y_n-1

The settings that should be used on NEOS are "Concorde data(xy-list file, L2 norm)", "Algorithm: Concorde(QSopt)", and "Random seed: fixed".

Baseline

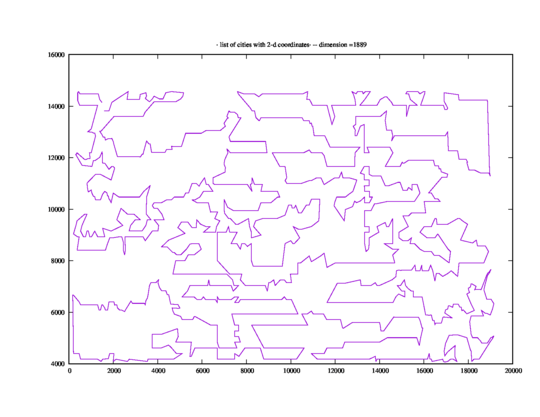
The 1,889-point instance rl1889.tsp from TSPLIB takes "Total Running Time: 871.18 (seconds)", which is more than five minutes. It looks like this:

Answer 1

88 Cities, 341 seconds runtime on NEOS

In a recent paper we constructed a family of hard to solve euclidean TSP instances. You can download the instances from this family as well as code for generating them here:

http://www.or.uni-bonn.de/%7Ehougardy/HardTSPInstances.html

The 88 city instance from this family takes Concorde on the NEOS server more than 5 minutes. The 178-city instance from this family takes already more than a day to solve.

Answer 2

77 cities, 7.24 minutes (434.4 seconds) average run time on NEOS

I’m a little late to the party, but I’d like to contribute a 77-node instance, weruSnowflake77.

I created this instance while trying to understand which local and global characteristics impose an upward pressure on the amount of time concorde takes to match its best lower bound with the length of its shortest found tour.

To construct this instance, I began with a base graph (13 x 13 square), and then systematically introduced new points or translated old points, retaining the adjustments that appeared to make concorde go deeper into its branches on average before cutting.

The technique is similar to the way a genetic algorithm mutates existing tours and retains shorter tours for the next generation of mutations, except the graph itself is being mutated and the harder-to-solve graphs are retained. It's also similar to the way we mutate graphs using relaxations to help construct good lower bounds, except I'm going the opposite way, mutating an existing graph to construct a graph with hard to find lower bounds.

In the process I’ve found a few smaller graphs that take concorde minutes to solve, but this is the first small graph I’ve found that takes concorde a minimum of 5 minutes.

With 10 trial runs on NEOS using the fixed seed and QSopt, the average runtime was 7.24 minutes (434.531 seconds). The minimum runtime was 5.6 minutes (336.64 seconds). The maximum runtime was 8.6 minutes (515.80 seconds). No trials were discarded. Full benchmark table below:

Benchmark results over 10 runs:

----------------------------------
| Run | Job ID# | Total running  |
|     |         | time (seconds) |
|-----|---------|----------------|
| 1   | 7739963 | 513.44         |
| 2   | 7740009 | 336.64         |
| 3   | 7740023 | 514.25         |
| 4   | 7740029 | 447.97         |
| 5   | 7740038 | 357.10         |
| 6   | 7740072 | 447.47         |
| 7   | 7740073 | 336.19         |
| 8   | 7740075 | 515.80         |
| 9   | 7740088 | 361.26         |
| 10  | 7740091 | 515.19         |
----------------------------------

weruSnowflake77 (x-y list, L2 norm):

77
-700 -700
700 -700
200 0
0 200
-200 0
0 -200
0 0
-600 600
-500 600
-400 600
-300 600
-200 600
-100 600
0 600
100 600
200 600
300 600
400 600
500 600
600 600
-600 -600
-500 -600
-400 -600
-300 -600
-200 -600
-100 -600
0 -600
100 -600
200 -600
300 -600
400 -600
500 -600
600 -600
600 -500
600 -400
600 -300
600 -200
600 -100
600 0
600 100
600 200
600 300
600 400
600 500
-600 -500
-600 -400
-600 -300
-600 -200
-600 -100
-600 0
-600 100
-600 200
-600 300
-600 400
-600 500
-500 -500
-400 -400
-300 -300
-200 -200
-100 -100
100 100
200 200
300 300
400 400
500 500
100 -100
200 -200
300 -300
400 -400
500 -500
-100 100
-200 200
-300 300
-400 400
-500 500
700 700
-700 700

Repository

• Github URL: https://github.com/LDubya/weruSnowflake77

Problem set files from repo:

• weruSnowflake77.txt (x-y list file, L2 norm)
• weruSnowflake77.tsp (TSPLIB format, EUC_2D)

Answer 3

Python 3, 911 cities, 1418 seconds of run time on NEOS

The following Python 3.x script generates the coordinates of 911 cities. It took NEOS 1418 seconds to calculate the shortest path of 47739.

Here is A picture of thee shortest path (thanks to A. Rex):

The code/algorithm is based on the Feigenbaum bifurcation, which I used to generate a series of values, which I used as a basis for generating the coordinates of the cities. I experimented with the parameters until I found a number of cities under 1000 that took NEOS a surprising amount of time (well above the required 5 minutes).

x = 0.579
coords = []
for _ in range(1301):
    if int(3001*x) not in coords:
        coords.append(int(3001*x))
    x = 3.8*x*(1-x)
coords = list(zip(coords, coords[::-1]))
print(len(coords))
for coord in coords:
    print(f"{coord[0]} {coord[1]}")

PS: I have a script running in search for a lower number of cities that also take >5 minutes on NEOS. I'll post them in this answer if I find any.

PS: Damn! Running this script with l parameter 1811 instead of 1301 results in 1156 cities with a running time on NEOS of just over 4 hours, which is a lot more than other cases with similar parameters...