Where is that snake going?

Question

Write a function (using as few bytes as possible) that takes a bi-dimensional array of any number of columns and rows in which:

• 0 represents empty block,
• 1 represents snake block.

The function must return the number of possible paths the snake traveled.

Example 1:

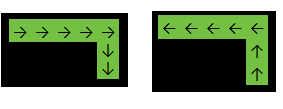
Input:

[
  [1,1,1,1,1],
  [0,0,0,0,1],
  [0,0,0,0,1],
]

Output: 2

In the example above, the function will return 2 because the answer is either one of:

Example 2:

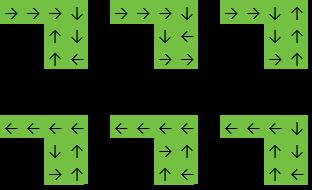
Input:

[
  [1,1,1,1],
  [0,0,1,1],
  [0,0,1,1],
]

Output: 6

In this example the function will return 6 because the answer is either one of:

Note:

When assessing the input, you can assume that:

• The arrays representing columns will always have the same sizes (so the arrays are rectangular);
• There exists at least 1 valid path;
• The snake cannot walk through the edges (as can happen in some versions of snake);
• The snake will always have at least 2 blocks;
• The snake cannot move diagonally;
• The paths are directed. (so, two paths ending at different positions but otherwise looking exactly the same are not the same path, it’ll add up to the total)

Answer 1

Wolfram Language (Mathematica), 16+83=99 bytes

Library import statement (16 bytes):

<<Combinatorica`

Actual function body (83 bytes):

Length@HamiltonianCycle[MakeGraph[#~Position~1~Join~{1>0},##||Norm[#-#2]==1&],All]&

Try it online!

---

Note that the question just ask for the number of Hamiltonian path in the graph.

However, (for some reason) the HamiltonianPath function doesn't really work with directed graph (example). So, I used the workaround described in this Mathematica.SE question:

• Add an vertex (called True) that is connected to all other vertices.
• Count the number of Hamiltonian cycle on the resulting graph.

The graph is constructed using MakeGraph (annoyingly there are no directly equivalent built-in), using the boolean function ##||Norm[#-#2]==1&, which returns True if and only if one of the arguments is True or the distance between the two vertices are 1.

---

Tr[1^x] cannot be used instead of Length@x, and <2 cannot be used instead of ==1.

---

HamiltonianPath can be used if the graph is undirected, with the function body takes 84 bytes (exactly 1 byte more than the current submission):

Length@HamiltonianPath[MakeGraph[#~Position~1,Norm[#-#2]==1&,Type->Undirected],All]&

Try it online!

Answer 2

Jelly, 12 11 bytes

ŒṪŒ!ạƝ€§ÐṂL

Try it online!

---

Explanation.

ŒṪ               Positions of snake blocks.
  Œ!             All permutations.
                 For each permutation:
    ạƝ€             Calculate the absolute difference for each neighbor pair
       §            Vectorized sum.
                 Now we have a list of Manhattan distance between snake
                    blocks. Each one is at least 1.
        ÐṂL      Count the number of minimum values.
                    Because it's guaranteed that there exists a valid snake,
                    the minimum value is [1,1,1,...,1].

Answer 3

JavaScript (ES6), 154 134 bytes

m=>m.map((r,Y)=>r.map(g=(_,x,y,r=m[y=1/y?y:Y])=>r&&r[x]&&[-1,0,1,2].map(d=>r[r[x]=0,/1/.test(m)?g(_,x+d%2,y+~-d%2):++n,x]=1)),n=0)|n/4

Try it online!

How?

Method

Starting from each possible cell, we flood-fill the matrix, clearing all cells on our way. Whenever the matrix contains no more 1's, we increment the number n of possible paths.

Each valid path is counted 4 times because of the direction chosen on the last cell, which actually doesn't matter. Therefore, the final result is n / 4.

Recursive function

Instead of calling the recursive function g() from the callback of the second map() like this...

m=>m.map((r,y)=>r.map((_,x)=>(g=(x,y,r=m[y])=>...g(x+dx,y+dy)...)(x,y)))

...we define the recursive function g() directly as the callback of map():

m=>m.map((r,Y)=>r.map(g=(_,x,y,r=m[y=1/y?y:Y])=>...g(_,x+dx,y+dy)...))

Despite the rather long formula y=1/y?y:Y which is needed to set the initial value of y, this saves 2 bytes overall.

Commented code

m =>                           // given the input matrix m[][]
  m.map((r, Y) =>              // for each row r[] at position Y in m[][]:
    r.map(g = (                //   for each entry in r[], use g() taking:
      _,                       //     - the value of the cell (ignored)
      x,                       //     - the x coord. of this cell
      y,                       //     - either the y coord. or an array (1st iteration),
                               //       in which case we'll set y to Y instead
      r = m[y = 1 / y ? y : Y] //     - r = the row we're currently located in
    ) =>                       //       (and update y if necessary)
      r && r[x] &&             //     do nothing if this cell doesn't exist or is 0
      [-1, 0, 1, 2].map(d =>   //     otherwise, for each direction d,
        r[                     //     with -1 = West, 0 = North, 1 = East, 2 = South:
          r[x] = 0,            //       clear the current cell
          /1/.test(m) ?        //       if the matrix still contains at least one '1':
            g(                 //         do a recursive call to g() with:
              _,               //           a dummy first parameter (ignored)
              x + d % 2,       //           the new value of x
              y + ~-d % 2      //           the new value of y
            )                  //         end of recursive call
          :                    //       else (we've found a valid path):
            ++n,               //         increment n
          x                    //       \_ either way,
        ] = 1                  //       /  do r[x] = 1 to restore the current cell to 1
      )                        //     end of map() over directions
    ),                         //   end of map() over the cells of the current row
    n = 0                      //   start with n = 0
  ) | n / 4                    // end of map() over the rows; return n / 4

Answer 4

Python 2, 257 246 241 234 233 227 214 210 bytes

lambda b:sum(g(b,i,j)for j,l in e(b)for i,_ in e(l))
e=enumerate
def g(b,x,y):d=len(b[0])>x>-1<y<len(b);c=eval(`b`);c[d*y][d*x]=0;return d and b[y][x]and('1'not in`c`or sum(g(c,x+a,y)+g(c,x,y+a)for a in(1,-1)))

Try it online!

---

Saved

• -8 bytes, thanks to Kevin Cruijssen
• -14 bytes, thanks to user202729

Answer 5

Python 2, 158 bytes

E=enumerate
g=lambda P,x,y:sum(g(P-{o},*o)for o in P if x<0 or abs(x-o[0])+abs(y-o[1])<2)+0**len(P)
lambda L:g({(x,y)for y,r in E(L)for x,e in E(r)if e},-1,0)

Try it online!

Answer 6

Haskell, 187 155 bytes

r=filter
l=length
(a,b)?(x,y)=abs(a-x)+abs(b-y)==1
l#x=sum[p!r(/=p)l|p<-x]
p![]=1
p!l=l#r(p?)l
f x|l<-[(i,j)|i<-[0..l x-1],j<-[0..l(x!!0)-1],x!!i!!j>0]=l#l

Try it online!