20
1
The challenge is to write codegolf for the permanent of a matrix.
The permanent of an n-by-n matrix A = (ai,j) is defined as
Here S_n represents the set of all permutations of [1, n].
As an example (from the wiki):
Your code can take input however it wishes and give output in any sensible format but please include in your answer a full worked example including clear instructions for how to supply input to your code. To make the challenge a little more interesting, the matrix may include complex numbers.
The input matrix is always square and will be at most 6 by 6. You will also need to be able to handle the empty matrix which has permanent 1. There is no need to be able to handle the empty matrix (it was causing too many problems).
Examples
Input:
[[ 0.36697048+0.02459455j, 0.81148991+0.75269667j, 0.62568185+0.95950937j],
[ 0.67985923+0.11419187j, 0.50131790+0.13067928j, 0.10330161+0.83532727j],
[ 0.71085747+0.86199765j, 0.68902048+0.50886302j, 0.52729463+0.5974208j ]]
Output:
-1.7421952844303492+2.2476833142265793j
Input:
[[ 0.83702504+0.05801749j, 0.03912260+0.25027115j, 0.95507961+0.59109069j],
[ 0.07330546+0.8569899j , 0.47845015+0.45077079j, 0.80317410+0.5820795j ],
[ 0.38306447+0.76444045j, 0.54067092+0.90206306j, 0.40001631+0.43832931j]]
Output:
-1.972117936608412+1.6081325306004794j
Input:
[[ 0.61164611+0.42958732j, 0.69306292+0.94856925j,
0.43860930+0.04104116j, 0.92232338+0.32857505j,
0.40964318+0.59225476j, 0.69109847+0.32620144j],
[ 0.57851263+0.69458731j, 0.21746623+0.38778693j,
0.83334638+0.25805241j, 0.64855830+0.36137045j,
0.65890840+0.06557287j, 0.25411493+0.37812483j],
[ 0.11114704+0.44631335j, 0.32068031+0.52023283j,
0.43360984+0.87037973j, 0.42752697+0.75343656j,
0.23848512+0.96334466j, 0.28165516+0.13257001j],
[ 0.66386467+0.21002292j, 0.11781236+0.00967473j,
0.75491373+0.44880959j, 0.66749636+0.90076845j,
0.00939420+0.06484633j, 0.21316223+0.4538433j ],
[ 0.40175631+0.89340763j, 0.26849809+0.82500173j,
0.84124107+0.23030393j, 0.62689175+0.61870543j,
0.92430209+0.11914288j, 0.90655023+0.63096257j],
[ 0.85830178+0.16441943j, 0.91144755+0.49943801j,
0.51010550+0.60590678j, 0.51439995+0.37354955j,
0.79986742+0.87723514j, 0.43231194+0.54571625j]]
Output:
-22.92354821347135-90.74278997288275j
You may not use any pre-existing functions to compute the permanent.
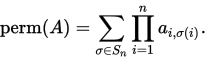
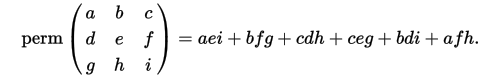
Is the matrix always a 3x3? Or are the dimensions arbitrary? – L. Steer – 2016-10-20T13:35:11.613
@L.Steer Updated question. Thank you. – None – 2016-10-20T13:36:00.643
Do we need to handle an empty matrix? – Jonathan Allan – 2016-10-20T13:53:29.127
@JonathanAllan Yes. Great question. – None – 2016-10-20T13:54:21.513
12Could you please remove the complex requirement? I think it ruins an otherwise nice challenge. Every language that doesn't have built-in complex arithmetic now has to do a totally separate task. – xnor – 2016-10-20T14:48:36.853
6If we need to handle the empty matrix, you should add it as a test case. The fact that you cannot really represent the 0x0 matrix with lists makes this a bit difficult. Personally, I'd just remove that requirement. – Dennis – 2016-10-20T15:07:11.683
2It would also be nice to explain what S_n is for the benefit of those who don't know. – Martin Ender – 2016-10-20T15:47:20.263
1The empty matrix has permanent 1, not 0, though I agree with Dennis about just not including it. – xnor – 2016-10-20T16:34:56.567
@xnor Argh.. I knew I would get that wrong. Thank you. – None – 2016-10-20T16:36:51.093
4There's no point putting something in the sandbox for 3 hours. Give it 3 days and people have a chance to give feedback. – Peter Taylor – 2016-10-20T16:43:17.600
1@PeterTaylor I hear you. There is also the issue that I just have some preferences for codegolf questions which not everyone agrees with. For example, I don't feel the need to make every question as easy for restricted esolangs as for higher level languages. – None – 2016-10-20T16:45:13.513
71. It's not just esolangs. Bash, e.g., can't even natively deal with floats. Excluding a language from the competition just because it lacks a certain numeric type, even if can effortlessly implement the desired algorithm, is just being picky for no good reason. 2. I'm still not sure about the empty matrix. Would it be
[[]](has one row, the empty matrix doesn't) or[](doesn't have depth 2, matrices do) in list form? – Dennis – 2016-10-20T16:53:35.757@Dennis 2. I think a 1d empty array is
[]and a 2d one is[[]]. I suppose equivalently we could define it to have one empty column. This is just an oddity of how 2d arrays are represented I think. 1. I love bash more than most people but surely almost all challenges have a set of languages that are suited to it and a set that aren't. I also don't think we should compare solutions in different languages in codegolf. I am interested in the best one in each language for which there is a submitted answer. – None – 2016-10-20T17:28:58.450@Dennis http://unix.stackexchange.com/a/40787 has various fun ways of handling floating point numbers.
– None – 2016-10-20T17:31:22.59741. I'm not daying that it's impossible to solve this challenge in Bash, but if the lion share of the code is used to deal with complex number arithmetic, it stops being a challenge about permanents. 2. Most if not all current answers is languages without a matrix type break for input
[[]]. – Dennis – 2016-10-20T17:56:14.1131
[[]]is clearly a 1x0 matrix. My recursive function needs the empty matrix as base case, and it comes naturally down to[]. - BTW, I think an example that is easy to type (low dimension, simple numbers) would have been very helpful. – Christian Sievers – 2016-10-20T18:30:47.083@ChristianSievers you are right on both counts. – None – 2016-10-20T18:35:09.797
1It's a shame this otherwise-great question is burdened by these difficulties. Like Peter said - leave challenges in the sandbox longer if you want good feedback. 3 hours is way too short. – Mego – 2016-10-20T23:45:13.317
@Mego I removed the empty matrix requirement. I hope that helps. – None – 2016-10-21T07:40:15.000
2My objection wasn't related to the empty matrix requirement (I made it after the requirement was removed). I am objecting to requiring complex number support (which doesn't really add anything to the challenge other than incredible complication for languages without native complex number support), the lack of simple test cases, and the lack of explanation for your equations (not everyone knows that
S_nrepresents the set of all permutations of[1, n]). – Mego – 2016-10-21T07:43:18.437@Mego I have now added an explanation for S_n (thank you. I used yours). Can we just disagree about the complex number requirement? I think it's interesting and it's an extra interesting challenge (in my view) to golf code in a language that doesn't have complex number support. No one should be comparing the length of such code with something in a language that does. In general, my preference is for challenges that are closer to real life problems and I feel there is room on codegolf for a wide variety of question types. – None – 2016-10-21T07:47:10.763
1@Lembik The issue is, as Dennis mentioned, by requiring complex number support, this challenge is more about complex number arithmetic than it is about the permanent of a matrix in languages without native complex number support. It's essentially two different challenges, depending on the choice of language. – Mego – 2016-10-21T08:05:13.630
1@Mego the same argument is valid for the tons of challenges on this site based on operation on prime numbers. Every esolang has a 1 byte builtin for the primality test, while using general purpose languages you have to add a bunch of code just to do the test – edc65 – 2016-10-21T08:49:30.400
3
@edc65 Those challenges include operations on prime numbers because they actually add something to the challenge (or are the core of the challenge). Requiring complex support in this challenge is adding unnecessary fluff by requiring the use of unnecessarily complicated number types, which causes it to be a chameleon challenge. Three hits on the "don't do these things" list is not good.
– Mego – 2016-10-21T08:54:37.4431
@Mego example: http://codegolf.stackexchange.com/questions/89726/golf-a-brain-flak-integer/90608#90608
– edc65 – 2016-10-21T23:48:04.810@edc65 Trying to say "well why didn't you complain about X challenge" isn't constructive - I don't read every challenge that gets posted. – Mego – 2016-10-22T05:43:57.437
1@Mego Don't you? You said "those challenges...". I did not complain about them (trust me, they are a lot) even if I don't like them, and I don't complain about this one. – edc65 – 2016-10-22T09:42:30.807