18
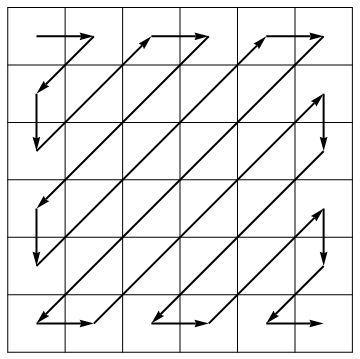
As part of its compression algorithm, the JPEG standard unrolls a matrix into a vector along antidiagonals of alternating direction:
Your task is to take the unrolled vector along with the matrix dimensions and reconstruct the corresponding matrix. As an example:
[1, 2, 5, 9, 6, 3, 4, 7, 1, 2, 8, 3], 4, 3
should yield
[1 2 3 4
5 6 7 8
9 1 2 3]
whereas dimensions 6, 2 would give
[1 2 6 3 1 2
5 9 4 7 8 3]
Rules
You may choose to take only one of the dimensions as input. The individual inputs can be taken in any order. You may assume that the width and height are positive and valid for the given vector length.
You may assume that the vector elements are positive integers less than 10.
You may write a program or function, taking input via STDIN (or closest alternative), command-line argument or function argument and outputting the result via STDOUT (or closest alternative), function return value or function (out) parameter.
The input vector may be given in any convenient, unambiguous, flat list or string format.
The output matrix may be in any convenient, unambiguous, nested list or string format, or as a flat list along with both matrix dimensions. (Or, of course, as a matrix type if your language has those.)
Standard code-golf rules apply.
Test Cases
Each test case is of the form vector width height => matrix.
[1] 1 1 => [[1]]
[1 2 3 1] 2 2 => [[1 2] [3 1]]
[1 2 3 1] 4 1 => [[1 2 3 1]]
[1 2 5 9 6 3 4 7 1 2 8 3] 3 4 => [[1 2 3] [5 6 4] [9 7 8] [1 2 3]]
[1 2 5 9 6 3 4 7 1 2 8 3] 4 3 => [[1 2 3 4] [5 6 7 8] [9 1 2 3]]
[1 2 5 9 6 3 4 7 1 2 8 3] 6 2 => [[1 2 6 3 1 2] [5 9 4 7 8 3]]
[1 2 5 9 6 3 4 7 1 2 8 3] 12 1 => [[1 2 5 9 6 3 4 7 1 2 8 3]]
[1 2 5 9 6 3 4 7 1 2 8 3] 1 12 => [[1] [2] [5] [9] [6] [3] [4] [7] [1] [2] [8] [3]]
Related Challenges
- Zigzagify a Matrix (the somewhat simpler inverse transformation)
- Rotate the anti-diagonals