Zigzagify a Matrix

Question

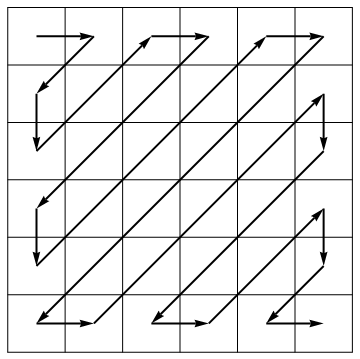
As part of its compression algorithm, the JPEG standard unrolls a matrix into a vector along antidiagonals of alternating direction:

Your task is to take a matrix (not necessarily square) and return it in unrolled form. As an example:

[1 2 3 4
 5 6 7 8
 9 1 2 3]

should yield

[1, 2, 5, 9, 6, 3, 4, 7, 1, 2, 8, 3]

Rules

You may assume that the matrix elements are positive integers less than 10.

You may write a program or function, taking input via STDIN (or closest alternative), command-line argument or function argument and outputting the result via STDOUT (or closest alternative), function return value or function (out) parameter.

The input matrix may be given in any convenient, unambiguous, nested list or string format, or as a flat list along with both matrix dimensions. (Or, of course, as a matrix type if your language has those.)

The output vector may be in any convenient, unambiguous, flat list or string format.

Standard code-golf rules apply.

Test Cases

[[1]]                                               => [1]
[[1 2] [3 1]]                                       => [1 2 3 1]
[[1 2 3 1]]                                         => [1 2 3 1]
[[1 2 3] [5 6 4] [9 7 8] [1 2 3]]                   => [1 2 5 9 6 3 4 7 1 2 8 3]
[[1 2 3 4] [5 6 7 8] [9 1 2 3]]                     => [1 2 5 9 6 3 4 7 1 2 8 3]
[[1 2 6 3 1 2] [5 9 4 7 8 3]]                       => [1 2 5 9 6 3 4 7 1 2 8 3]
[[1 2 5 9 6 3 4 7 1 2 8 3]]                         => [1 2 5 9 6 3 4 7 1 2 8 3]
[[1] [2] [5] [9] [6] [3] [4] [7] [1] [2] [8] [3]]   => [1 2 5 9 6 3 4 7 1 2 8 3]

Related Challenges

• Reconstruct a zigzagified matrix (the somewhat trickier inverse transformation)
• Rotate the anti-diagonals

Answer 1

J, 31 30 14 12 11 bytes

[:;<@|.`</.

Ych. Too big.

Takes a matrix as input.

Explanation

J has an advantage here. There's a command called oblique (/.) which takes the oblique lines in turn and applies a verb to them. In this case I'm using a gerund to apply two verbs alternately: < (box) and <@|. (reverse and box). Then it's just a matter of unboxing everything using ; (raze).

Answer 2

Jelly, 24 19 15 13 11 bytes

pS€żị"¥pỤị⁵

Takes number of rows, number of columns and a flat list as separate command-line arguments.

Try it online!

How it works

pS€żị"¥pỤị⁵  Main link. Argument: m (rows), n (columns), A (list, flat)

p            Compute the Cartesian product [1, ..., m] × [1, ..., n]. This yields
             the indices of the matrix M, i.e., [[1, 1], [1, 2], ..., [m, n]].
 S€          Compute the sums of all index pairs.
       p     Yield the Cartesian product.
      ¥      Dyadic chain. Arguments: Sums, Cartesian product.
    ị"       For each index pair in the Cartesian product, retrieve the coordinate
             at the index of its sum, i.e., map [i, j] to i if i + j is odd and to
             j if i + j is even.
   ż         Zip the sums with the retrieved indices.
       Ụ     Sort [1, ..., mn] by the corresponding item in the resulting list.
        ị⁵   Retrieve the corresponding items from A.

Answer 3

Pyth, 24 23 21 20 19 18 17 bytes

ssm_W=!Td.T+LaYkQ

Alternate 17-byte version: ssuL_G=!T.T+LaYkQ

                Q  input
           +L      prepend to each subarray...
             aYk   (Y += ''). Y is initialized to [], so this prepends [''] to
                     the first subarray, ['', ''] to the second, etc.
                   ['' 1  2  3  4
                    '' '' 5  6  7  8
                    '' '' '' 9  1  2  3]
         .T        transpose, giving us
                   ['' '' ''
                    1  '' ''
                    2  5  ''
                    3  6  9
                    4  7  1
                    8  2
                    3]
  m_W=!Td          black magic
 s                 join subarrays together
s                  join *everything* on empty string (which means ''s used for
                     padding disappear)

Thanks to @FryAmTheEggman for a byte, @Jakube for 2 bytes, and @isaacg for a byte!

Explanation of "black magic" alluded to above: m_W=!Td essentially reverses every other subarray. It does this by mapping _W=!T over each subarray; W is conditional application, so it _s (reverses) all subarrays where =!T is true. T is a variable preinitialized to ten (truthy), and =!T means (T = !T). So it toggles the value of a variable that starts out truthy and returns the new value, which means that it will alternate between returning falsy, truthy, falsy, truthy... (credit to Jakube for this idea)

Test suite here.

Answer 4

MATL, 28 27 bytes

tZyZ}:w:!+-1y^7MGn/*-X:K#S)

Adapted from my answer here. The general idea is to create a 2D array of the same size as the input, filled with values that increase in the same order as the zig-zag path. Then the linearized (flattened) version of that array is sorted, and the indices of that sorting are kept. Those are the indices that need to be applied to the input in order to produce the zig-zag path.

Input is in the form

[1 2 3; 5 6 4; 9 7 8; 1 2 3]

Explanation

Try it online!

t       % input 2D array. Duplicate
ZyZ}    % get size as length-2 vector. Split into two numbers: r, c
:       % range [1,2,...,c] as a row vector
w:!     % swap, range [1;2;...;r] as a column vector
+       % add with broadcast. Gives a 2D array
-1      % push -1
y^      % duplicate previous 2D array. Compute -1 raised to that
7M      % push [1;2;...;r] again
Gn/     % divide by input matrix size, that is, r*c
*       % multiply
-       % subtract
X:      % linearize 2D array into column array
K#S     % sort and push the indices of the sorting. Gives a column vector
)       % index input matrix with that column vector

Answer 5

Matlab, 134 bytes

I just tried my best to shorten my code in Matlab, like telegraphing it.

function V=z(M)
[m,n]=size(M);
a=(1:m)'*ones(1,n);
b=ones(m,1)*(1:n);
A=a+b-1;
B=a-b;
C=(A.^2+(-1).^A.*B+1);
[~,I]=sort(C(:));
V=M(:);
V=V(I)';

Notes:

1. M is an m×n matrix.
2. a and b are both matrices same size of M, each row of a consists of numbers equal to its row number, while each column of b is equal to its column number. Thus, a+b is a matrix whose element equals to sum of its row and column number, i.e., matrix(p,q)=p+q.
3. Thus, A(p,q)=p+q-1; and B(p,q)=p-q.
4. C is mathematically stated as equation below. with the equation, a zigzagifiedly increasing matrix can be made like shown below.

C =
     1     2     6     7
     3     5     8    14
     4     9    13    18
    10    12    19    25

5. C indicates the order of elements of M in zigzagified results. Then, [~,I]=sort(C(:));returns the order, i.e., I, thus, V=V(I)' is the result.

Answer 6

JavaScript (SpiderMonkey 30+), 99 bytes

x=>[for(y of[...x,...x[0]].keys())for(z of Array(y+1).keys())if(a=x[y%2?z:y-z])if(b=a[y%2?y-z:z])b]

Tested in Firefox 44. Takes input as a 2D array.

Answer 7

Python 2, 84 bytes

lambda N,w,h:[N[i*w+s-i]for s in range(w+h+1)for i in range(h)[::s%2*2-1]if-1<s-i<w]

Porting nimi's answer. Takes a flat array with given width and height. xsot saved a byte.

---

88 bytes:

lambda M,w,h:[M[i]for i in sorted(range(w*h),key=lambda i:(i/w+i%w,-i*(-1)**(i/w+i%w)))]

Takes a flat array with given width and height. Sorts the corresponding 2D coordinates (i/w,i%w) in zigzag order of increasing sum to get diagonals, tiebroken by either increasing or decreasing row value, based on whether the row plus column is odd or even.

Answer 8

Haskell, 79 78 73 bytes

(m#h)w=[m!!(y*w+x-y)|x<-[0..h+w],y<-g!!x$[0..x],y<h,x-y<w]
g=reverse:id:g

The input is a flat list with the number of rows and columns, e.g. ( [1,2,6,3,1,2,5,9,4,7,8,3] # 2) 6 -> [1,2,5,9,6,3,4,7,1,2,8,3].

How it works: walk through the x and y coordinates of the matrix (h rows, w columns) in two nested loops:

  | 0 1 2 3 4 5 6 7 8    outer loop               Index is y*w+x-y, i.e.
--+------------------    x from 0 to h+w          the elements are accessed
0 | 1 2 6 3 1 2                                   in the following order:
1 | 5 9 4 7 8 3
2 |                                               1 2 4 6  8 10 
3 |                                               3 5 7 9 11 12
4 |
5 |
6 |
7 | inner loop:
8 | y from 0 to x

i.e. from top/right to down/left, skipping out of bound indices (y and x must satisfy y<h and x-y<w). When x is even, the order of the inner loop is reversed: y goes from x to 0. I do this by picking a modifying function for the y-range [0..x] which is the xth element of [reverse,id,reverse,id,...].

Edit: @xnor re-arranged the loops and saved 5 bytes. Thanks!

Answer 9

Python 2 + NumPy, 122 bytes

I admit it. I worked ahead. Unfortunately, this same method cannot be easily modified to solve the other 2 related challenges...

import numpy
def f(m):w=len(m);print sum([list(m[::-1,:].diagonal(i)[::(i+w+1)%2*-2+1])for i in range(-w,w+len(m[0]))],[])

Takes a numpy array as input. Outputs a list.

Try it online

Explanation:

def f(m):
    w=len(m)    # the height of the matrix, (at one point I thought it was the width)
    # get the anti-diagonals of the matrix. Reverse them if odd by mapping odd to -1
    d=[list(m[::-1,:].diagonal(i)[::(i+w+1)%2*-2+1])for i in range(-w,w+len(m[0]))]
            # w+len(m[0]) accounts for the width of the matrix. Works if it's too large.
    print sum(d,[]) # join the lists

A lambda is the same length:

import numpy
lambda m:sum([list(m[::-1,:].diagonal(i)[::(i+len(m)+1)%2*-2+1])for i in range(-len(m),len(m)+len(m[0]))],[])

Answer 10

Python 3, 131 118 115 107 bytes

Based on the same principe as my answer of Deusovi's challenge

I assume we can't have zero in the input matrice

e=enumerate
lambda s:[k for j,i in e(zip(*[([0]*n+i+[0]*len(s))for n,i in e(s)]))for k in i[::j%2*2-1]if k]

Explanation

how it works :

            pad with 0      transpose    remove 0    reverse line           concatenate 
                                                     with even index
1 2 3       1 2 3 0 0        1 0 0        1            1                
4 5 6   --> 0 4 5 6 0    --> 2 4 0    --> 2 4     -->  2 4              -->  1 2 4 7 5 3 6 8 9
7 8 9       0 0 7 8 9        3 5 7        3 5 7        7 5 3             
                             0 6 8        6 8          6 8               
                             0 0 9        9            9

Results

>>> [print([i,f(i)]) for i in [[[1]], [[1, 2], [3, 1]], [[1, 2, 3, 1]], [[1, 2, 3], [5, 6, 4], [9, 7, 8], [1, 2, 3]], [[1, 2, 3, 4], [5, 6, 7, 8], [9, 1, 2, 3]], [[1, 2, 6, 3, 1, 2], [5, 9, 4, 7, 8, 3]], [[1, 2, 5, 9, 6, 3, 4, 7, 1, 2, 8, 3]], [[1], [2], [5], [9], [6], [3], [4], [7], [1], [2], [8], [3]]]]
# [input,                                                          output]
[[[1]],                                                            [1]]
[[[1, 2], [3, 1]],                                                 [1, 2, 3, 1]]
[[[1, 2, 3, 1]],                                                   [1, 2, 3, 1]]
[[[1, 2, 3], [5, 6, 4], [9, 7, 8], [1, 2, 3]],                     [1, 2, 5, 9, 6, 3, 4, 7, 1, 2, 8, 3]]
[[[1, 2, 3, 4], [5, 6, 7, 8], [9, 1, 2, 3]],                       [1, 2, 5, 9, 6, 3, 4, 7, 1, 2, 8, 3]]
[[[1, 2, 6, 3, 1, 2], [5, 9, 4, 7, 8, 3]],                         [1, 2, 5, 9, 6, 3, 4, 7, 1, 2, 8, 3]]
[[[1, 2, 5, 9, 6, 3, 4, 7, 1, 2, 8, 3]],                           [1, 2, 5, 9, 6, 3, 4, 7, 1, 2, 8, 3]]
[[[1], [2], [5], [9], [6], [3], [4], [7], [1], [2], [8], [3]],     [1, 2, 5, 9, 6, 3, 4, 7, 1, 2, 8, 3]]