Find the powertrain!

Question

The winner (pretty obviously) is Dennis ♦, who used Jelly with 10 bytes!

This challenge will still be up here, however results won't be taken anymore.

---

The powertrain of a number is a concept by John Conway (who is also notable for making Conway's Game of Life, but that's not the point). It is defined as so:

For any number 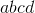..., the powertrain of the number is 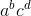... (i.e. every 2nd digit, from left to right, is a power of the digit before that). This process is repeated until the result is a single digit.

EXAMPLES:

2592 => (2^5)(9^2) = 2592 <= Cannot be further decomposed 135 => (1^3)5 = 5 1234 => (1^2)(3^4) = 81 => (8^1) = 8 1100 => (1^1)(0^0) = 1 # (0^0) = 1 -42 => -42 # Negative numbers output the input

Your challenge is, for any number n in the input, return powertrain(n) (i.e. n after the powertrain decomposition is finished) as output.

This is code golf, so shortest amount of bytes wins.

DISCLAIMER-THINGS:

• You can have an odd number of digits in the input, the last digit just won't have a power.
• 0^0 is 1, because if it was 0, then a lot of numbers would instantly collapse to 0 or 1.
• If the number is indestructible in any part of the computation process (e.g. if it ends up with 2592), then you can just output the number.
• If the input is < 10 (i.e. all single digit numbers and negatives), output the input.

I'll probably announce a winner after a few hours days.

Current leaderboard:

1. Jelly (Dennis ♦): 10
2. Pyth (DenkerAffe): 16
3. MATL (Don Muesli): 21
4. Perl (Ton Hospel): 42
5. Haskell (Damien): 64
6. Javascript ES6 (edc65): 71
7. Mathematica (murphy): 74
8. Mathematica (LegionMammal978) and Haskell (Renzeee): 77
9. Python 2 (mathmandan): 111
10. Python 3 (Erwan): 161
11. Java 8 (Blue): 229
12. Oracle SQL 11.2 (Jeto): 456
13. Befunge '93 (Lex): 490

Answer 1

Jelly, 15 14 12 10 bytes

Ds2*/€Pµ³¡

Try it online!

How it works

Ds2*/€Pµ³¡  Main link. Argument: n

D           Convert n into the array of its decimal digits.
 s2         Split into pairs of digits.
   */€      Reduce each pair by exponentiation.
      P     Take the product of the resulting powers.
       µ    Push the preceding chain as a link, and start a new one.
        ³¡  Execute the link n times and return the last result.

Answer 2

Haskell, 67 64 bytes

(>>=(==))>>=until$p.show is an unnamed function taking an integer as input and returning its powertrain.

Saved 3 bytes thanks to Zgarb

p(x:y:r)=p[x]^p[y]*p r;p[]=1;p x=read x
(>>=(==))>>=until$p.show

Answer 3

Perl, 42 48 bytes

Include +2 for -lp (you can drop the -l too but I like newlines)

Run with input on STDIN, e.g.

perl -lp powertrain.pl <<< 1234

powertrain.pl:

s/\B/1&pos?"**":"*"/eg until++$.>($_=eval)

(on older perls you can also drop the space between the regex and until)

This won't be able to handle the fixed point 24547284284866560000000000 but that large a value won't work anyways because by that time perl switched to exponential notation.

The above version is will in fact work fast (at most 2592 loops) for all numbers that perl can represent without using exponential notation since it is proven that there are no fixed points between 2592 and 24547284284866560000000000 (https://oeis.org/A135385)

This does however assume something as yet unproven. In principle there could be a reduction that takes more than X=10^7 steps (it is conjectured that no non-fixed point takes more than 16 steps, https://oeis.org/A133503) whose value dips below X (but above 10^7) and then goes up again. If that is the case I must fall back to:

s/\B/1&pos?"**":"*"/eg until$s{$_=eval}++||/-/

Explanation

The code works by putting ** and * (alternating) between the digits

s/\B/1&pos?"**":"*"/eg

so 2592 becomes 2**5*9**2 and 12345 becomes 1**2*3**4*5. These are valid perl expressions that can be evaluated with

$_ = eval

(0**0 is 1 in perl). Then just put a loop around that with a counter that makes it expire. Since except for the fixed points the values go down extremely quickly the powertrain series converges before the counter gets a chance to really get going

Answer 4

Pyth, 25 18 11 16 bytes

?<Q0Qu*F^McjGT2Q

Try it here!

7 14 bytes saved with help from @Jakube

Explanation

?<Q0Qu*F^McjGT2Q   # Q = eval(input)

?<Q0Q              # If input is negative return Q
     u         Q   # apply the following function until we reach a cycle               
                   # starting value is Q and the current value is in G
           jGT     # split input into a list of digits
          c   2    # split into pairs of 2
        ^M         # compute the power for every pair
      *F           # compute the product of all powers

Answer 5

Python 2, 111 bytes

def p(n,b=0,o=''):
 if n<1:return n
 for c in str(n):o+=c+'**'[b:];b=~b
 j=eval(o+'1');return p(j)if j-n else j

The idea is to make a string where the digits of n are separated by operations which alternate between * and **, and then eval that string. (Other solutions use this same idea; see for example Ton Hospel's Perl answer.)

So, the operation switches back and forth between '**'[0:], which is **, and '**'[-1:], which is just *.

However, by the end of the for-loop, the string ends with an operation (one or the other), so we either need to drop the last operation, or else add another digit, in order for the string to make sense.

Fortunately, appending a 1 on the end will work no matter which operation is last. (If you like, 1 is a one-sided identity from the right, for both multiplication and exponentiation. Another way of saying this is that powertrain(n) == powertrain(10*n + 1) for all n>0.)

Finally, if the result of the eval happens to be the same as the input (as in a length-1 cycle), the function terminates. Otherwise, the function calls itself on the result. (It will hang forever on any cycle of length > 1, but according to the OP's comments I am allowed to assume there are no such cycles.)

(Note: the above explanation works for single-digit positive integers, since a single-digit input n will be completed to n**1 which will result in a 1-cycle. However, we also need to accept non-positive input, so there's a condition at the beginning that short-circuits if the input is less than 1. We could eliminate that line, and save 17 bytes, if the input were guaranteed to be non-negative.)

Answer 6

Java 8, 265 244 229 bytes

This is my first answer, but I have been reading this site for a while and think I know what I'm doing. At least it beats befunge and SQL...

Unfortunately, like other answers, this one does not work for 24547284284866560000000000 due to java'a built in restrictions on how large integers can get.

Saved 36 bytes thanks to @JackAmmo

public int p(int n){if(n<10)return n;int i=1,t=1,s=(int)Math.log10(n)+1,r[]=new int[s];for(;i<=s;){int a=(int)Math.pow(10,i);r[s-i++]=n%a/(a/10);}for(i=0;i<s-1;i++)t*=Math.pow(r[i],r[++i]);if(s%2==1)t*=r[s-1];return n==t?n:p(t);}

Ungolfed Explanation

public int powertrain(int input){
    //handles negative and 1-digit cases
    if(input<10)return input;
    //initialize output variable       
    int total=1;
    // get "length" of number. Shorter than getting length of string representation
    int size=(int)Math.log10(input)+1;
    //initialize array to store digits
    int[] array=new int[size];
    //Now, because Java doesn't have support
    // for the "**" operation, and the way of turning
    // an integer into a string takes too many bytes,
    // I decided just to put every digit into an array with
    // math and iterate from there
    for(int i=1;i<=size;){
        int place=(int)Math.pow(10,i);
        //crazy math. Saved 1 byte by incrementing i when accessed
        array[size-i++]=input%place/(place/10);
    }
    for(int i=0;i<size-1;i++)
        //This is where the train happens.
        //Saved 1 byte by incrementing while accessing 
        //again, instead of i+=2 and i+1
        total*=Math.pow(array[i],array[++i]);
    //Make sure last number isn't left out if size is odd
    if(size%2==1)
        total*=array[size-1];
    //if we end up with same number, stop.
    //otherwise, keep recurring
    return input==total?input:powertrain(total);
}

Answer 7

JavaScript (ES6) 71

A recursive function, stopping when a repetition is found. This could not work for longer loops (2 or more value repeating) but it seems this could not happen, at least in the limited range of javascript number precision (17 digits)

f=n=>[...n+'1'].map((c,i)=>i&1?r*=Math.pow(d,c):d=c,r=1)&&n-r?f(r):n

Test

f=n=>[...n+'1'].map((c,i)=>i&1?r*=Math.pow(d,c):d=c,r=1)&&n-r?f(r):n

function go()
{
  v=+I.value
  R.textContent=f(v)
}  

go()

<input id=I value="1234"><button onclick="go()">Go</button>
<span id=R></span>

Answer 8

Haskell, 100 79 77 bytes

g x|x==h x=x|1<2=g$h x;h=i.map(read.(:[])).show;i[]=1;i[a]=a;i(a:b:c)=a^b*i c

Not golfed:

g x|x==h x=x|1<2=g$h x
h=i.map(read.(:[])).show
i[]=1
i[a]=a
i(a:b:c)=a^b*i c

This function splits the input into digits and does the trick via i.

EDIT: Thanks to nimi for some tips.

Answer 9

MATL, 21 bytes

tt0>*:"V!UtQgv9L2#)^p

It may take a few seconds to produce the output.

EDIT (July 30, 2016): the linked code replaces 9L by 1L to adapt to recent changes in the language.

Try it online!

This uses the following two tricks to reduce byte count at the expense of code efficiency:

• Iterate n times instead of waiting until a cycle is found. This is acceptable as per OP's comments.
• For an odd number of digits a final 1 would have to be appended to complete the final power operation. Instead of that, the number of added 1 is the number of digits. This ensures an even number, so all power operations can be done (even if the last ones are unnecessary 1^1 operations).

Code:

t         % implicitly take input x. Duplicate
t0>*      % duplicate. Is it greater than 0? Multiply. This gives 0 if input is negative,
          % or leaves the input unchanged otherwise
:         % Generate array [1,2,...,x]
"         % for each (repeat x times)
  V       %   convert x to string
  !       %   transpose into column char array
  U       %   convert each char into number
  tQg     %   duplicate. Add 1 so that no entry is zero. Convert to logical: gives ones
  v       %   concatenate vertically
  9L2#)   %   separate odd-indexed and even-indexed entries
  ^       %   element-wise power
  p       %   product of all entries
          % implicitly end for each
          % implicitly display

Answer 10

Mathematica, 77 bytes

Times@@(If[#2<1,1,#^#2]&)@@@Partition[IntegerDigits@#,2,2,1,1]&~FixedPoint~#&

Anonymous function. Not too complicated.

Answer 11

Befunge 720 490 bytes

Couldn't resist to do one more after the Never tell me the odds thing. So, I've optimized the "ASCII-fier" of the previous one. In this case I saw no need to let the instruction pointer run over the digits to read them, so I haven't taken the effort to make them human readable. So it's more of a digitifier, now.

Again, if you guys want an explanation, let me know in the comments, I'll try to create some helpful descriptions. You can copy paste the code into the interpreter. I've found that the example 24547284284866560000000000 outputs 0, but that seems to be a problem with getting such a large value from a point on the grid, as you can clearly see the correct value being stored in the final steps.

v                                                    //top row is used for "variables"
>&:0`#v_.@                                           //initialize the counter                          
v     <                           g01_v#-p01:  <     //on our way back to the digitifier, check if we're done
>::>210p>55+%:10g0p-55+/:v            >10g.@         //digitifier, creates a series of ASCII characters at the top line, one for each digit in the source
        ^p01+1g01    _v#:<
v1$$                  <                              //forget some remainders of the digitifier, put 1 on the stack as a base of calculation
                      v p0-1g01-1g0-1g01*g0g01<      //taking powers of each pair of digit
>10g2-!#v_10g1-!#v_  1>                10g1-0g|
^                                  p01-2g01  *<
        >10g0g*  >                             ^     //extra multiplication with last digit if the number of digits was odd

This version also supports negative input. It's a great improvement on the previous version, if I say so myself. At least 1 bug was fixed and the size was reduced greatly.

Answer 12

Mathematica, 74 bytes

0~f~0=f[]=1
f@n_=n
f[a_,b_,c___]:=f[c]a^b
#//.i_/;i>0:>f@@IntegerDigits@i&

Explanation

This solution uses a helper function f, which takes the digits of the number as arguments and applies one iteration of the power train operation. The last line is a pure function that is crafted to exploit the ReplaceRepeated function (or //. for short), which applies a rule to an expression (in this case the argument # of the pure function) until it doesn't change anymore. The rule i_/;i>0:>f@@IntegerDigits@i replaces anything non-negative with the function f applied to its decimal digits.

Answer 13

Python 3, 169 161 bytes

def f(s):
 o=[['1',s]['-'in s]]
 while s not in o:
  o+=[s];s+='1'*(len(s)%2==1);r=1;
  for i,j in zip(s[::2],s[1::2]):r*=int(i)**int(j);s=str(r);
 return o[-1]

Ungoldfed

def f(s):
 o=[['1',s]['-'in s]]
 while s not in o:
  o+=[s]
  s+='1'*(len(s)%2==1)
  r=1
  for i,j in zip(s[::2],s[1::2]):
   r*=int(i)**int(j)
  s=str(r)
 return o[-1]

Results

>>> [f(i) for i in ['135', '1234', '642', '2592', '-15']]
['5', '8', '2592', '2592', '-15']

Answer 14

Oracle SQL 11.2, 456 bytes

WITH v(n,c,i,f,t)AS(SELECT:1+0,CEIL(LENGTH(:1)/2),1,'1',0 FROM DUAL UNION ALL SELECT DECODE(SIGN(c-i+1),-1,t,n),DECODE(SIGN(c-i+1),-1,CEIL(LENGTH(t)/2),c),DECODE(SIGN(c-i+1),-1,1,i+1),DECODE(SIGN(c-i+1),-1,'1',RTRIM(f||'*'||NVL(POWER(SUBSTR(n,i*2-1,1),SUBSTR(n,i*2,1)),SUBSTR(n,i*2-1,1)),'*')),DECODE(SIGN(c-i+1),-1,0,TO_NUMBER(column_value))FROM v,XMLTABLE(f)WHERE i<=c+2 AND:1>9)CYCLE n,c,i,f,t SET s TO 1 DEFAULT 0SELECT NVL(SUM(n),:1) FROM v WHERE s=1;

Un-golfed

WITH v(n,c,i,f,t) AS
(
  SELECT :1+0,CEIL(LENGTH(:1)/2),1,'1',0 FROM DUAL
  UNION ALL
  SELECT DECODE(SIGN(c-i+1),-1,t,n),
         DECODE(SIGN(c-i+1),-1,CEIL(LENGTH(t)/2),c),
         DECODE(SIGN(c-i+1),-1,1,i+1),
         DECODE(SIGN(c-i+1),-1,'1',RTRIM(f||'*'||NVL(POWER(SUBSTR(n,i*2-1,1),SUBSTR(n,i*2,1)),SUBSTR(n,i*2-1,1)),'*')),
         DECODE(SIGN(c-i+1),-1,0,TO_NUMBER(column_value))
  FROM v,XMLTABLE(f) WHERE i<=c+2 AND :1>9 
)  
CYCLE n,c,i,f,t SET s TO 1 DEFAULT 0
SELECT NVL(SUM(n),:1) FROM v WHERE s=1;

v is a recursive view, parameters are

n : number to split in 2 digits parts

c : number of 2 digits parts

i : current 2 digits part to compute

f : string concatenating the powers with * as separator

t : evaluation of f

The DECODEs switch to the next number to split and compute when all the parts of the current number are done.

XMLTABLE(f) takes an expression an evaluates it, putting the result in the pseudo column "column_value". It's the golfed version of http://tkyte.blogspot.fr/2010/04/evaluating-expression-like-calculator.html

CYCLE is the oracle build in cycle detection and is used as the exit condition.

Since the result for :1<10 is :1 and v returns no row for those cases, SUM forces a row with NULL as the value. NVL returns :1 as the result if the row is null.