1
Energy levels of electrons
Electrons are ordered into "shells". However, sometimes electrons get excited, for example by heat, and leave their shell to go to another! These electrons will go back at some point, but they cannot go back to their original shell without emitting energy in the form of radio waves.
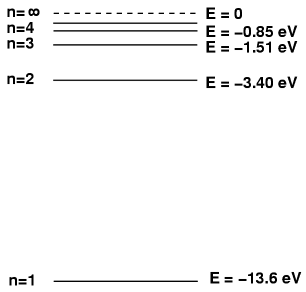
For example, the energy levels for hydrogen look like this:
The base energy level of an electron in hydrogen is at n = 1. If it gets 'excited', it might go to n = 4. However, on the way back, the electron does not always simply go from n = 4 to n = 1, it has different options. See the example.
Task
Write a program or function that takes an integer and outputs the amount of options the electron has to get back to its un-excited state. For this task, you can take granted that an electron can only emit energy from its excited state. It will not get more energy once it has been excited.
This is code-golf, the answer with the least amount of bytes wins.
If you are interested in these type of questions, check out this similar question. Also check out this for more info on these matters.
Input
The input of your function/program is a whole integer. It is greater than 0 and less than 2^31.
Output
An integer, the amount of options the electron has to return to its original state, which is n = 1 (for hydrogen). When the input is 1, return 0, as it is already in its original energy level.
Examples
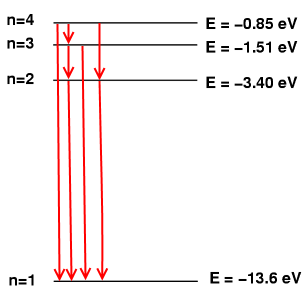
Input: 4
Output: 4
Because the options are:
4 -> 3 -> 2 -> 1
4 -> 3 -> 1
4 -> 2 -> 1
4 -> 1
Visualised:
18
When I saw "the electron does not always simply go from n = 4 to n = 1" http://i.imgur.com/FNxsSSC.png
– DanTheMan – 2015-10-21T16:00:46.600@DanTheMan I didn't get the joke... – user41805 – 2015-10-21T18:46:51.777
8The simple mathematical expression for the solution makes the whole problem rather silly. Before posting a challenge, you should write code to generate test cases, and here it would have let you catch the pattern. – xnor – 2015-10-21T19:34:31.623
1
To add to what @xnor said, it's also a good idea to post challenges to the Sandbox. That way people can offer useful feedback before the challenge goes live.
– Alex A. – 2015-10-22T05:26:40.990Thanks for the feedback, ill make use of your proposals next time. – Thomas W – 2015-10-22T07:49:56.177
5I'm voting to close this question as off-topic because it's too narrow - there's a simple mathematical formula to solve it, no ingenuity involved. – isaacg – 2015-10-22T08:11:25.477