39
10
User CarpetPython posted a new take on this problem which puts a much bigger focus on heuristic solutions, due to an increased search space. I personally think that challenge is much nicer than mine, so consider giving that one a try!
Vector racing is an addictive game that can be played with a pen and a sheet of square-ruled paper. You draw an arbitrary racetrack on the paper, define a start and end and then you steer your point-sized car in a turn-based manner. Get to the end as fast as you can, but be careful not to end up in a wall!
The Track
- The map is a two dimensional grid, where each cell has integer coordinates.
- You move on the grid cells.
- Each grid cell is either part of the track or it's a wall.
- Exactly one track cell is the starting coordinate.
- At least one track cell is designated as the goal. Landing on any of these completes the race. Multiple goal cells are not necessarily connected.
Steering the Car
Your car starts at a given coordinate and with velocity vector (0, 0). In each turn, you may adjust each component of the velocity by ±1 or leave it as is. Then, the resulting velocity vector is added to your car's position.
A picture may help! The red circle was your position last turn. The blue circle is your current position. Your velocity is the vector from the red to the blue circle. In this turn, depending on how you adjust your velocity, you may move to any of the green circles.
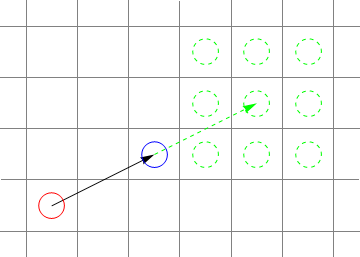
If you land in a wall, you lose immediately.
Your task
You guessed it: write a program which, given a racetrack as input, steers the car to one of the goal cells in as few turns as possible. Your solution should be able to deal reasonably well with arbitrary tracks and not be specifically optimised towards the test cases provided.
Input
When your program is invoked, read from stdin:
target
n m
[ASCII representation of an n x m racetrack]
time
target is the maximum number of turns you may take to complete the track, and time is your total time budget for the track, in seconds (not necessarily integer). See below for details about timing.
For the newline-delimited track, the following characters are used:
#– wallS– the start*– a goal.– all other track cells (i.e. road)
All cells outside the n x m grid provided are implied to be walls.
The coordinate origin is in the top left corner.
Here is a simple example:
8
4.0
9 6
###...***
###...***
###...***
......###
S.....###
......###
Using 0-based indexing, the starting coordinate would be (0,4).
After every move you will receive further input:
x y
u v
time
Where x, y, u, v are all 0-based integers. (x,y) is your current position and (u,v) is your current velocity. Note that x+u and/or y+v could be out of bounds.
time is whatever is left of your time budget, in seconds. Feel free to ignore this. This is only for participants who really want to take their implementation to the time limit.
When the game is over (because you've landed in a wall, moved out of bounds, exceeded target turns, ran out of time or reached the goal), you'll receive an empty line.
Output
For each turn, write to stdout:
Δu Δv
where Δu and Δv each are one of -1, 0, 1. This will be added to (u,v) to determine your new position. Just to clarify, the directions are as follows
(-1,-1) ( 0,-1) ( 1,-1)
(-1, 0) ( 0, 0) ( 1, 0)
(-1, 1) ( 0, 1) ( 1, 1)
An optimal solution for the above example would be
1 0
1 -1
1 0
Note that the controller does not attach itself to stderr, so you're free to use it for any sort of debug output you may need while developing your bot. Please remove/comment out any such output in your submitted code, though.
Your bot may take half a second to respond in each single turn. For turns that take longer, you will have a time budget (per track) of target/2 seconds. Every time a turn takes longer than half a second, the additional time will be subtracted from your time budget. When your time budget hits zero the current race will be aborted.
New: For practical reasons, I have to set a memory limit (since memory seems to be more limiting than time for reasonable track sizes). Therefore, I will have to abort any test run where the racer uses more than 1GB of memory as measured by Process Explorer as Private Bytes.
Scoring
There is a benchmark of 20 tracks. For each track:
- If you complete the track, your score is the number of moves you need to reach a goal cell divided by
target. - If you run out of time/memory or don't reach the goal before
targetturns have elapsed or you land in a wall/out of bounds at any time, your score is2. - If your program is not deterministic, your score is the average over 10 runs on that track (please state this in your answer).
Your overall score is the sum of the individual track scores. Lowest score wins!
Furthermore, every participant may (and is strongly encouraged to) provide an additional benchmark track, which will be added to the official list. Previous answers will be re-evaluated including this new track. This is to make sure that no solution is tailored too closely to the existing test cases and to account for interesting edge cases I might have missed (but which you may spot).
Tie breaking
Now that there is already an optimal solution, this will probably be the main factor for participants' scores.
If there is a tie (due to several answers solving all tracks optimally or otherwise), I will add additional (larger) test cases to break the tie. To avoid any human bias when creating those tie-breakers, these will be generated in a fixed manner:
- I will increase the side length
nby10compared to the last track generated this way. (I may skip sizes if they don't break the tie.) - The basis is this vector-graphic
- This will be rasterised at the desired resolution using this Mathematica snippet.
- The start is in the top left corner. In particular, it will be the left-most cell of the top-most row of that end of the track.
- The goal is in the bottom right corner. In particular, it will be the right-most cell of the bottom-most row of that end of the track.
- The
targetwill4*n.
The final track of the initial benchmark was already generated like this, with n = 50.
The Controller
The program that tests the submissions is written in Ruby and can be found on GitHub along with the benchmark file I'll be using. There is also an example bot called randomracer.rb in there, which simply picks random moves. You can use its basic structure as a starting point for your bot to see how the communication works.
You can run your own bot against a track file of your choice as follows:
ruby controller.rb track_file_name command to run your racer
e.g.
ruby controller.rb benchmark.txt ruby randomracer.rb
The repository also contains two classes Point2D and Track. If your submission is written in Ruby, feel free to reuse those for your convenience.
Command-line switches
You can add command-line switches -v, -s, -t before the benchmark's file name. If you want to use multiple switches, you can also do, for instance, -vs. This is what they do:
-v (verbose): Use this to produce a little more debug output from the controller.
-s (silent): If you prefer to keep track of your position and velocity yourself and don't care about the time budget, you can switch off those three lines of output each turn (sent to your submission) with this flag.
-t (tracks): Lets you select individual tracks to be tested. E.g. -t "1,2,5..8,15" would test tracks 1, 2, 5, 6, 7, 8 and 15 only. Thanks a lot to Ventero for this feature and the options parser.
Your submission
In summary, please include the following in your answer:
- Your score.
- If you're using randomness, please state this, so I can average your score over multiple runs.
- The code for your submission.
- The location of a free compiler or interpreter for your language of choice that runs on a Windows 8 machine.
- Compilation instructions if necessary.
- A Windows command-line string to run your submission.
- Whether your submission requires the
-sflag or not. - (optionally) A new, solvable track which will be added to the benchmark. I will determine a reasonable
targetfor your track manually. When the track is added to the benchmark, I'll edit it out of your answer. I reserve the right to ask you for a different track (just in case you add an disproportionally large track, include obscene ASCII art in the track, etc.). When I add the test case to the benchmark set, I'll replace the track in your answer with a link to the track in the benchmark file to reduce the clutter in this post.
As you can see, I'll be testing all submissions on a Windows 8 machine. If there is absolutely no way to get your submission running on Windows, I can also try on a Ubuntu VM. This will be considerably slower though, so if you want to max out the time limit, make sure your program runs on Windows.
May the best driver emerge vectorious!
But I wanna play!
If you want to try out the game yourself to get a better feel for it, there is this implementation. The rules used there are slightly more sophisticated, but it is similar enough to be useful, I think.
Leaderboard
Last updated: 01/09/2014, 21:29 UTC
Tracks in benchmark: 25
Tie-breaker sizes: 290, 440
- 6.86688 – Kuroi Neko
- 8.73108 – user2357112 - 2nd submission
- 9.86627 – nneonneo
- 10.66109 – user2357112 - 1st submission
- 12.49643 – Ray
- 40.0759 – pseudonym117 (probabilistic)
Detailed test results. (The scores for probabilistic submissions have been determined separately.)
erf... My barebone allocator is just a bit too barebone. I'll add the necessary crap to make it work with g++, then. Sorry about that. – None – 2014-08-31T13:23:29.923
OK, that's fixed. The g++ version even actually works about 30% faster. It now outputs some stats on stderr. Feel free to comment it out (from the last lines of the source). Sorry again for the blunder. – None – 2014-08-31T16:11:16.100
Alright, it works now and I reproduced your score. It's damn fast! :) I'll add your test case to the benchmark, but I'll change the target to
400, as that's in line with how I determined all the other targets (except the tie breaker). I'll update the main post once I've reran all the other submissions. – Martin Ender – 2014-08-31T20:13:40.150Updated the results. There was no need for a tie breaker, because all other submissions exceed the memory limit on your test track. Congrats on that! :) – Martin Ender – 2014-08-31T20:32:00.453
Thanks. Actually this challenge gave me an occasion to dig into these STL hash tables. Though I hate C++ guts, I can't help but getting killed by my curiosity. Meow! :). – None – 2014-08-31T20:41:13.270
Nice submission. I wonder if I'd have to switch languages to beat it, or if algorithmic optimizations and microoptimizations would do it. – user2357112 supports Monica – 2014-09-01T02:44:11.453
@MartinBüttner: I've added a second racer to my submission, this time using bidirectional search. It seems to just barely squeeze by under the memory limit for the new track, though I don't expect it to win the tiebreakers. – user2357112 supports Monica – 2014-09-01T02:46:23.893
@user2357112 Thanks for letting me know, I'll rerun tests tonight. – Martin Ender – 2014-09-01T07:37:27.807
@user2357112 The BFS approach is a brute. Clearly a smarter algorithm should defeat it. I was thinking of enforcing stricter memory limits (maybe 100Mb or so), so that you won't need huge maps to tell smarter algorithms apart from the current winning brutes :) – None – 2014-09-01T10:12:39.883
@kuroineko I don't think I want to change the limits again more than 2 months after the challenge was posted. I guess I'll just have to live with running huge test sets now. – Martin Ender – 2014-09-01T19:12:20.820
Well bad news then, I just finished another refinement of my BFS that beats the 100x400 map in 1.5s and consumes just over 200 Mb :). I can post it to another answer if you like. I would rather not overwrite the other answer to keep the discussions about hash tables, since the new version does without any. – None – 2014-09-01T19:31:41.057
@user2357112 (and kuroi) I've updated the results. user2357112's new submission hits the memory limit at a tie-breaker of size 440. interestingly, nneonneo's submission doesn't have a problem with that, and hence overtakes your old submission again. kuroi's still has lots of room in any case. kuroi, post another version if you want, but currently there's no need since you're very clearly leading anyway. of course, if you do I'll have no choice but run more tests later this week. – Martin Ender – 2014-09-01T20:35:15.340
lol I would not want to overburden you. I'd rather explore a few possibilities before publishing a new source. I'm thinking of adding some kind of preprocessing to reduce the BFS search space. Btw my current version hits the 1Gb limit for a 100x1050 map similar to the one I posted. – None – 2014-09-01T21:40:39.513