Count the terminal cycles of a directed graph

Question

Task

You must write a program or function in the language of your choice which accurately counts the number of terminal cycles of a simple directed graph.

This particular kind of directed graph is represented as an array of n integers, each with an independently-chosen random value between 1 and n (or 0 and n-1, if your language counts from 0). The graph can be thought of as arrows pointing from one index (node) to an index which matches the value found at the starting index.

Your function must be capable of accepting large graphs, up to n=1024, or any smaller integer size.

Example

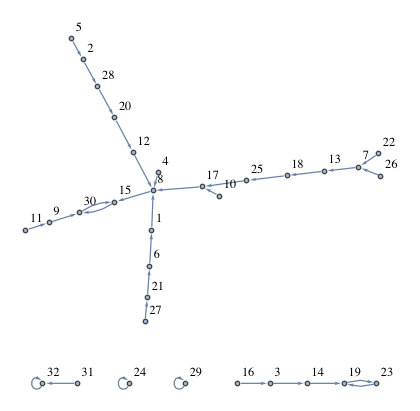
Consider this graph for n=10:

[9, 7, 8, 10, 2, 6, 3, 10, 6, 8]

Index 1 contains a 9, so there's an arrow from index 1 to index 9. Index 9 contains a 6, so there's an arrow 9 -> 6. Index 6 contains 6, which is a terminal cycle, pointing back to itself.

Index 2 contains a 7. Index 7 contains a 3. Index 3 contains an 8. Index 8 contains a 10. Index 10 contains an 8, so that's a second terminal cycle (8 -> 10 -> 8 -> 10, etc.).

Index 4 -> 10, which enters the second terminal cycle. Likewise, index 5 -> 2 -> 7 -> 3 -> 8, which is also part of the second terminal cycle.

At this point, all indices (nodes) have been checked, all paths have been followed, and two unique terminal cycles are identified. Therefore, the function should return 2, since that is the number of terminal cycles in this directed graph.

Scoring

Aim for the smallest code, but make sure it counts terminal cycles correctly. Shortest code after 1 week wins.

Test Cases

Here's are some test cases to check the correctness of your code. If your language counts array indices starting from 0, you must of course subtract 1 from the value of each array element, to prevent an out-of-bound index.

n=32, 5 cycles:

[8, 28, 14, 8, 2, 1, 13, 15, 30, 17, 9, 8, 18, 19, 30, 3, 8, 25, 23, 12, 6, 7, 19, 24, 17, 7, 21, 20, 29, 15, 32, 32]

n=32, 4 cycles:

[20, 31, 3, 18, 18, 18, 8, 12, 25, 10, 10, 19, 3, 9, 18, 1, 13, 5, 18, 23, 20, 26, 16, 22, 4, 16, 19, 31, 21, 32, 15, 22]

n=32, 3 cycles:

[28, 13, 17, 14, 4, 31, 11, 4, 22, 6, 32, 1, 13, 15, 7, 19, 10, 28, 9, 22, 5, 26, 17, 8, 6, 13, 7, 10, 9, 30, 23, 25]

n=32, 2 cycles:

[25, 23, 22, 6, 24, 3, 1, 21, 6, 18, 20, 4, 8, 5, 16, 10, 15, 32, 26, 25, 27, 14, 13, 12, 9, 9, 29, 8, 13, 31, 32, 1]

n=32, 1 cycle:

[6, 21, 15, 14, 22, 12, 5, 32, 29, 3, 22, 23, 6, 16, 20, 2, 16, 25, 9, 22, 13, 2, 19, 20, 26, 19, 32, 3, 32, 19, 28, 16]

n=32, 1 cycle:

[8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 1, 2, 3, 4, 5, 6, 7]

n=1024, 6 cycles:

[239, 631, 200, 595, 178, 428, 582, 191, 230, 551, 223, 61, 564, 463, 568, 527, 143, 403, 154, 236, 928, 650, 14, 931, 236, 170, 910, 782, 861, 464, 378, 748, 468, 779, 440, 396, 467, 630, 451, 130, 694, 167, 594, 115, 671, 853, 612, 238, 464, 771, 825, 471, 167, 653, 561, 337, 585, 986, 79, 506, 192, 873, 184, 617, 4, 259, 4, 662, 623, 694, 859, 6, 346, 431, 181, 703, 823, 140, 635, 90, 559, 689, 118, 117, 130, 248, 931, 767, 840, 158, 696, 275, 610, 217, 989, 640, 363, 91, 129, 399, 105, 770, 870, 800, 429, 473, 119, 908, 481, 337, 504, 45, 1011, 684, 306, 126, 215, 729, 771, 5, 302, 992, 380, 824, 868, 205, 807, 917, 407, 759, 181, 640, 685, 795, 258, 180, 900, 20, 773, 546, 866, 564, 761, 632, 895, 968, 980, 651, 225, 676, 18, 685, 784, 208, 227, 3, 267, 852, 57, 487, 566, 633, 849, 309, 543, 145, 575, 811, 621, 560, 492, 24, 665, 66, 851, 168, 262, 259, 754, 481, 565, 768, 172, 1012, 241, 3, 370, 985, 389, 82, 779, 744, 829, 836, 249, 975, 909, 840, 226, 867, 499, 192, 909, 972, 735, 252, 785, 545, 486, 186, 1011, 89, 939, 649, 110, 119, 185, 836, 717, 545, 938, 621, 946, 94, 363, 721, 177, 747, 59, 819, 146, 283, 821, 547, 654, 941, 755, 18, 449, 367, 499, 944, 62, 553, 435, 344, 900, 25, 251, 920, 902, 99, 326, 98, 495, 385, 929, 865, 327, 725, 674, 33, 173, 429, 873, 558, 90, 460, 366, 543, 583, 954, 792, 213, 536, 670, 49, 738, 802, 1015, 23, 915, 119, 263, 307, 601, 474, 971, 826, 613, 446, 37, 145, 894, 901, 307, 906, 886, 990, 89, 798, 384, 487, 822, 354, 768, 902, 163, 179, 134, 920, 439, 619, 215, 94, 709, 744, 366, 543, 349, 347, 2, 438, 141, 486, 19, 998, 500, 857, 955, 932, 1, 587, 195, 646, 550, 887, 626, 400, 348, 154, 808, 678, 873, 186, 282, 168, 993, 722, 56, 345, 5, 226, 328, 22, 894, 658, 264, 13, 803, 791, 359, 217, 997, 168, 578, 952, 734, 964, 898, 659, 628, 980, 15, 31, 439, 13, 875, 687, 1004, 1023, 165, 642, 561, 897, 711, 124, 404, 346, 723, 774, 352, 784, 276, 395, 14, 443, 343, 153, 510, 590, 172, 215, 130, 106, 295, 906, 133, 758, 483, 898, 391, 760, 702, 972, 721, 611, 592, 1001, 724, 934, 59, 831, 171, 253, 869, 431, 538, 20, 648, 76, 351, 103, 33, 385, 852, 437, 470, 95, 434, 408, 430, 994, 366, 706, 809, 532, 161, 388, 668, 245, 965, 365, 913, 471, 927, 245, 256, 805, 540, 380, 995, 446, 657, 545, 573, 955, 499, 322, 949, 635, 401, 185, 421, 626, 534, 429, 930, 633, 563, 348, 626, 518, 682, 233, 775, 444, 42, 199, 57, 271, 683, 397, 883, 620, 768, 8, 331, 497, 19, 340, 900, 919, 497, 276, 78, 252, 164, 764, 927, 242, 270, 759, 824, 945, 886, 262, 59, 439, 217, 720, 519, 862, 626, 326, 339, 589, 16, 565, 947, 604, 144, 87, 520, 256, 240, 336, 685, 361, 998, 805, 678, 24, 980, 203, 818, 855, 85, 276, 822, 183, 266, 347, 8, 663, 620, 147, 189, 497, 128, 357, 855, 507, 275, 420, 755, 131, 469, 672, 926, 859, 156, 127, 986, 489, 803, 433, 622, 951, 83, 862, 108, 192, 167, 862, 242, 519, 574, 358, 549, 119, 630, 60, 925, 414, 479, 330, 927, 94, 767, 562, 919, 1011, 999, 908, 113, 932, 632, 403, 309, 838, 341, 179, 708, 847, 472, 907, 537, 516, 992, 944, 615, 778, 801, 413, 653, 690, 393, 452, 394, 596, 545, 591, 136, 109, 942, 546, 57, 626, 61, 587, 862, 829, 988, 965, 781, 849, 843, 815, 60, 928, 784, 388, 341, 491, 565, 83, 110, 164, 38, 1024, 859, 297, 520, 327, 733, 699, 631, 78, 178, 671, 895, 818, 637, 99, 425, 933, 248, 299, 333, 144, 323, 105, 849, 942, 767, 265, 72, 204, 547, 934, 916, 304, 919, 273, 396, 665, 452, 423, 471, 641, 675, 60, 388, 97, 963, 902, 321, 826, 476, 782, 723, 99, 735, 893, 565, 175, 141, 70, 918, 659, 935, 492, 751, 261, 362, 849, 593, 924, 590, 982, 876, 73, 993, 767, 441, 70, 875, 640, 567, 920, 321, 46, 938, 377, 905, 303, 736, 182, 626, 899, 512, 894, 744, 254, 984, 325, 694, 6, 367, 532, 432, 133, 938, 74, 967, 725, 87, 502, 946, 708, 122, 887, 256, 595, 169, 101, 828, 696, 897, 961, 376, 910, 82, 144, 967, 885, 89, 114, 215, 187, 38, 873, 125, 522, 884, 947, 962, 45, 585, 644, 476, 710, 839, 486, 634, 431, 475, 979, 877, 18, 226, 656, 573, 3, 29, 743, 508, 544, 252, 254, 388, 873, 70, 640, 918, 93, 508, 853, 609, 333, 378, 172, 875, 617, 167, 771, 375, 503, 221, 624, 67, 655, 465, 272, 278, 161, 840, 52, 1016, 909, 567, 544, 234, 339, 463, 621, 951, 962, 1019, 383, 523, 279, 780, 838, 984, 999, 29, 897, 564, 762, 753, 393, 205, 31, 150, 490, 156, 796, 586, 676, 773, 465, 489, 1024, 433, 214, 701, 480, 604, 280, 241, 563, 943, 911, 12, 400, 261, 883, 999, 207, 618, 141, 959, 767, 978, 461, 992, 982, 272, 143, 404, 645, 331, 348, 783, 698, 827, 82, 145, 536, 449, 852, 750, 789, 413, 913, 420, 14, 499, 285, 533, 223, 75, 591, 994, 884, 237, 63, 411, 563, 611, 801, 173, 759, 278, 318, 772, 1018, 48, 440, 333, 611, 834, 423, 583, 22, 716, 393, 794, 83, 83, 864, 859, 600, 525, 808, 569, 95, 952, 852, 567, 651, 2, 984, 906, 992, 747, 602, 143, 547, 1008, 940, 245, 633, 378, 193, 771, 965, 648, 437, 873, 591, 664, 271, 777, 274, 742, 68, 429, 825, 144, 55, 272, 279, 6, 400, 485, 66, 311, 663, 441, 23, 988, 726, 48, 624, 302, 617, 120, 653, 810, 641, 142]

Answer 1

GolfScript, 25 characters

:I{{I=.}I.+,*]I,>$0=}%.&,

Same approach as Keith Randall's solution but in GolfScript. Note that GolfScript has zero-indexed arrays. Online tester.

:I        # Assign input to variable I
{         # Foreach item in I
  {I=.}   # Code block: take the n-th list item
  I.+,*   # Iterate the code block 2*len(I) times
  ]       # and gather result in an array
  I,>     # Take last len(I) items
  $0=     # Get minimum
}%
.&        # Take unique items
,         # Count

Answer 2

Mathematica 69

Code

This finds the number of graph components.

f@l_ := Length@WeaklyConnectedComponents@Graph@Thread[Range@Length@l -> l]

---

The first test case:

v = {8, 28, 14, 8, 2, 1, 13, 15, 30, 17, 9, 8, 18, 19, 30, 3, 8, 25, 23, 12, 6, 7, 19, 24, 17, 7, 21, 20, 29, 15, 32, 32}
f[v]

5

---

Analysis

Make a list of directed edges between indices, (using example 1).

Thread[Range@Length@v -> v

{1 -> 8, 2 -> 28, 3 -> 14, 4 -> 8, 5 -> 2, 6 -> 1, 7 -> 13, 8 -> 15, 9 -> 30, 10 -> 17, 11 -> 9, 12 -> 8, 13 -> 18, 14 -> 19, 15 -> 30, 16 -> 3, 17 -> 8, 18 -> 25, 19 -> 23, 20 -> 12, 21 -> 6, 22 -> 7, 23 -> 19, 24 -> 24, 25 -> 17, 26 -> 7, 27 -> 21, 28 -> 20, 29 -> 29, 30 -> 15, 31 -> 32, 32 -> 32}

---

Graph draws a graph showing the graph components.

ImagePadding and VertexLabels are used here to show the indices.

Graph[Thread[Range[Length@v] -> v], ImagePadding -> 30, VertexLabels -> "Name"]

WeaklyConnectedComponents returns the list of vertices for each component.

Length returns the number of components.

c = WeaklyConnectedComponents[g]
Length[c]

{{17, 10, 25, 8, 18, 1, 4, 12, 15, 13, 6, 20, 30, 7, 21, 28, 9, 22, 26, 27, 2, 11, 5}, {14, 3, 19, 16, 23}, {32, 31}, {24}, {29}}

5

---

Timing of sample list with 1024 elements:

Timing: 0.002015 sec

f[z] // AbsoluteTiming

{0.002015, 6}

---

Just for fun, here's a picture of the final test case, graphed. I omitted the vertex labels; there are too many.

Graph[Thread[Range[Length@z] -> z], GraphLayout -> "RadialEmbedding"]

Answer 3

Python, 132 116 chars

def T(V):
 n=len(V);r=range(n);s={}
 for i in r:
    p=[i]
    for k in r+r:p+=[V[p[-1]]]
    s[min(p[n:])]=1
 return len(s)

For each index, we follows edges for n hops, which guarantees we are in a terminal cycle. We then follow n more hops and find the minimum index in that cycle. The total number of terminal cycles is then just the number of different minima we find.

Answer 4

In Python:

def c(l):
    if(l==[]):
        return 0
    elif (l[-1]==len(l)):
        return c(l[:-1])+1
    else:
        return c([[x,l[-1]][x==len(l)] for x in l[:-1]])

Answer 5

J - 61 53 char

This one was a doozy.

#@([:#/.~[:+./ .*"1/~@e.<~.@(],;@:{~)^:_&.>])@:(<@<:)

The <@<: turn the list into a J graph, which looks like a list of boxes, and the box at index i contains all the nodes that node i connects to. J indexes from zero, so we use <: to decrement everything by one before boxing with <.

   (<@<:) 9 7 8 10 2 6 3 10 6 8
+-+-+-+-+-+-+-+-+-+-+
|8|6|7|9|1|5|2|9|5|7|
+-+-+-+-+-+-+-+-+-+-+

The <~.@(],;@:{~)^:_&.>] turns each node into a list of all the nodes that can be reached from it. The <...&.>] is responsible for making this happen to each node, and the ~.@(],;@:{~)^:_ actually comes from a J golf of this 'nodes reachable' task I did a couple of weeks ago.

   (<~.@(],;@:{~)^:_&.>])@:(<@<:) 9 7 8 10 2 6 3 10 6 8
+---+-------+---+---+---------+-+-----+---+-+---+
|8 5|6 2 7 9|7 9|9 7|1 6 2 7 9|5|2 7 9|9 7|5|7 9|
+---+-------+---+---+---------+-+-----+---+-+---+

e. performs an interesting task. If the "reachability" closure of the graph (the version of the graph such that if there are directed edges X→Y and Y→Z we add the edge X→Z.) has N nodes and E edges, then e. on this graph makes a boolean matrix of N rows and E columns, with a True if the corresponding node shares a reachable node with this edge. Confusing, but bear with me.

   ([:e.<~.@(],;@:{~)^:_&.>])@:(<@<:) 9 7 8 10 2 6 3 10 6 8
1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0
0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 0 1 1
0 0 0 0 1 1 1 1 1 1 0 0 0 1 1 0 0 1 1 1 1 0 1 1
0 0 0 0 1 1 1 1 1 1 0 0 0 1 1 0 0 1 1 1 1 0 1 1
0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1 1
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0
0 0 0 1 1 1 1 1 1 1 0 0 1 1 1 0 1 1 1 1 1 0 1 1
0 0 0 0 1 1 1 1 1 1 0 0 0 1 1 0 0 1 1 1 1 0 1 1
0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0
0 0 0 0 1 1 1 1 1 1 0 0 0 1 1 0 0 1 1 1 1 0 1 1

Next, we have to find the number of terminal cycles, i.e. the number of groups that share Trues amongst their columns. We want to make sort of a multiplication table of the rows ("1/~), and we use a kind of inner product as the multiplication, one that ANDs pairwise and then ORs all the results together (+./ .*). The resulting matrix is a square table with a True in each position that two rows share at least one column between them.

   ([:+./ .*"1/~@e.<~.@(],;@:{~)^:_&.>])@:(<@<:) 9 7 8 10 2 6 3 10 6 8
1 0 0 0 0 1 0 0 1 0
0 1 1 1 1 0 1 1 0 1
0 1 1 1 1 0 1 1 0 1
0 1 1 1 1 0 1 1 0 1
0 1 1 1 1 0 1 1 0 1
1 0 0 0 0 1 0 0 1 0
0 1 1 1 1 0 1 1 0 1
0 1 1 1 1 0 1 1 0 1
1 0 0 0 0 1 0 0 1 0
0 1 1 1 1 0 1 1 0 1

Now all that's left to do is to check how many different kinds of row patterns there are. So we do exactly that: group together rows of the same kind (/.~), report the number in each group (#), and then take the number of groups (#@).

   #@([:#/.~[:+./ .*"1/~@e.<~.@(],;@:{~)^:_&.>])@:(<@<:) 9 7 8 10 2 6 3 10 6 8
2

Usage on other examples:

   tcc =: #@([:#/.~[:+./ .*"1/~@e.<~.@(],;@:{~)^:_&.>])@:(<@<:)  NB. name
   tcc 8 28 14 8 2 1 13 15 30 17 9 8 18 19 30 3 8 25 23 12 6 7 19 24 17 7 21 20 29 15 32 32
5
   tcc 20 31 3 18 18 18 8 12 25 10 10 19 3 9 18 1 13 5 18 23 20 26 16 22 4 16 19 31 21 32 15 22
4
   tcc 6 21 15 14 22 12 5 32 29 3 22 23 6 16 20 2 16 25 9 22 13 2 19 20 26 19 32 3 32 19 28 16
1
   tcc tentwentyfour  NB. the 1024-node example
6

Unfortunately the 1024 element case now takes a really long time to terminate. The previous version <:@#@((#~0={.+/@:*"1])^:a:)@e.@(~.@(],;@:{~)^:_&.>~<)@:(<@<:) (61 char) took a little over a second to do this.

Answer 6

Python (96)

Very, very, very, very based on user2228078's answer, as it works exactly the same, but is more golfed:

c=lambda l:(1+c(l[:-1])if l[-1]==len(l)else c([[x,l[-1]][x==len(l)]for x in l[:-1]]))if l else 0

(Technical question: should a golfing of someone elses answer be community wiki?)

Answer 7

Python (89) (87)

def c(G):
 u=i=0
 for _ in G:
  j=i;i+=1
  while j>=0:G[j],j=~i,G[j]
  u+=j==~i
 return u

The main idea is to start at each node at turn and walk along the path from it, marking each node we visit with a label unique to the node we started at. If we ever hit a marked node, we stop walking, and check if the marking is the one corresponding to our starting node. If it is we must have walked a loop, so we increment the count of cycles by one.

In the code, u is the cycle counter, i is the starting node, j is the current node we're walking. The label corresponding to starting node i is its bit-complement ~i which is always negative. We mark a node by pointing it to that value, overwriting whatever node it actually pointed to (being careful to walk to that node before it's forgotten).

We know we've hit a marked node when we walk to a negative-value "node" immediately afterwards. We check if that negative value is the current label to see whether we've walked a cycle. Since each node we walk is effectively deleted, each cycle will only be walked once.

It saves characters to count up i manually with a dummy loop variable _ then as for i in range(len(G)). Python lists are 0-indexed. If they were instead 1-indexed, we could save two characters by writing j=i=i+1 to have i and j be 1 for the first loop, and write j>0 in place of j>=0.

Edit:

We can save two characters by iterating i over the elements of the list rather than the indices, since node that are not pointed to by any edge don't matter. We have to iterate over set(G) though to avoid repeating a start node that it pointed to by multiple other nodes.

def c(G):
 u=0
 for i in set(G):
  j=i
  while j>=0:G[j],j=~i,G[j]
  u+=j==~i
 return u