C — aiming for clarity, didn't attempt to squeeze the code
Considering input:
A: A ∈ ℝ, A ≥ 1.0
B: B ∈ ℕ, B ≥ 1
Then there should usually be only one solution in ℝ, which simplifies the problem considerably.
Code is:
#include <stdlib.h>
#include <stdio.h>
#include <math.h>
#define TOLERANCE 1.0e-09
double tetrate(double, int);
int main(int argc, char **argv)
{
double target, max, min, mid, working;
int levels;
if (argc == 3)
{
target = atof(argv[1]); // A
levels = atoi(argv[2]); // B
// Shortcut if B == 1
if (levels == 1)
{
printf("%f\n", target);
return 0;
}
// Get a first approximation
max = 2.0;
while (tetrate(max, levels) < target)
max *= 2.0;
min = max / 2.0;
// printf("Answer is between %g and %g\n", min, max);
// Use bisection to get a closer approximation
do
{
mid = (min + max) / 2.0;
working = tetrate(mid, levels);
if (working > target)
max = mid;
else if (working < target)
min = mid;
else
break;
}
while (max - min > TOLERANCE);
// printf("%g: %f = %f tetrate %d\n", target, tetrate(mid, levels), mid, levels);
printf("%f\n", mid);
}
return 0;
}
double tetrate(double d, int i)
{
double result = d;
// If the result is already infinite, don't tetrate any more
while (--i && isfinite(result))
result = pow(d, result);
return result;
}
To compile:
gcc -o tet_root tet_root.c -lm
To run:
./tet_root A B
E.g.:
42
$ ./tet_root 65536 4
2.000000
33
$ ./tet_root 7625597484987 3
3.000000
3π
$ ./tet_root 1.340164183e18 3
3.141593
n(2½) ➙ 2 as n ➙ ∞ ? (well known limit)
$ ./tet_root 2 10
1.416190
$ ./tet_root 2 100
1.414214
$ ./tet_root 2 1000
1.414214
Yes!
n(e1/e) ➙ ∞ as n ➙ ∞ ? (upper bounds)
$ ./tet_root 9.999999999e199 100
1.445700
$ ./tet_root 9.999999999e199 1000
1.444678
$ ./tet_root 9.999999999e199 10000
1.444668
$ ./tet_root 9.999999999e199 100000
1.444668
Cool! (e1/e ≅ 1.44466786101...)
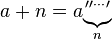
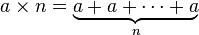
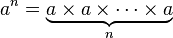
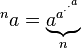
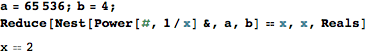
@user8777 The Bth super-root of A is equal to x if x^^B = A. – Simply Beautiful Art – 2017-09-19T17:07:16.263
1Are there minimum/maximum bounds on the input numbers? Should a valid answer support floating point answers, or only integer? – Josh – 2014-02-07T15:32:10.963
3If multiple solutions, should the program find all or just one? – Johannes H. – 2014-02-07T15:37:37.953
If answers must support floating point results, how many decimal places are required? Could you provide sample input/output for a few test cases? – Iszi – 2014-02-07T15:40:21.057
I've edited the question, I'm sorry but I can't provide any input/output sample. – Andrea Ciceri – 2014-02-07T15:56:30.343
5So what is your winning criteria? – Mhmd – 2014-02-07T17:27:09.543
2Can you give a simple example of a super-root that has more than one solution for a given A and B ≥ 1? – Tobia – 2014-02-07T20:39:40.093
@Tobia - I think there is only one solution in the real domain for that input range. In the complex domain there might be many solutions, but I let the MathLab folks deal with that... – None – 2014-02-07T21:31:36.543
@Tobia - And there is a limit of 1 for <sup>n</sup>0 for even n, so for A = 1, B = 2m there could be two roots: 0 or 1 (I think, but I'm not sure). – None – 2014-02-07T21:47:53.600
Ops, I've chosen the wrong tag, this is a code golf. @YiminRong - You're right, I've changed the question, now the program must find the only solution in the real domain. – Andrea Ciceri – 2014-02-07T22:02:30.167
1Can you give the mathematical representation of a super-root? I'm afraid I still don't understand how it is defined. – None – 2014-02-11T02:30:35.770