23
2
Bowling
Bowling is a game where, essentially, each player gets 10 turns to:
Take 2 attempts at knocking down 10 pins arranged in a triangle.
- between turns the pins are reset
- from the 1st to the 2nd attempt the pins are left as-is
The arrangement of the pins resembles the following scheme, with the pins numbered 0-9:
6 7 8 9
3 4 5
1 2
0
(Some rules and scoring mechanics omitted.)
Split spare
In bowling, a spare is when the player manages to knock down the pins that were left standing after a first attempt. A spare is said to be a split spare1 if the pins that were left standing are not adjacent.
E.g. if the pins are laid out as such:
. . 8 9
. . .
. 2
.
Then a player who manages to knock down all these 3 pins would score a split spare, given that the pin 2 is not adjacent to the 8, 9 group.
(1 for the purposes of this challenge, a split spare is defined taking into account only the adjacency of the pins left standing, even though Wikipedia's link states that for a split spare to take place, the pin 0 must have been knocked down already)
Your task
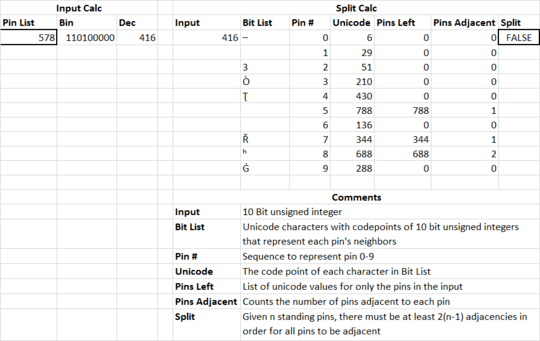
Given the numbers of the pins left standing, output a Truthy value if such an arrangement would give a split spare and Falsy otherwise.
Input
The list of all pins left standing (at least 2), in any reasonable format. Pin numbering may be 0- or 1-indexed provided it follows the numbering direction shown above. Sensible input formats include:
- a list of integers, like
[2, 8, 9] - a string of integers, like
"289" - separate arguments to a function
- an integer whose bits correspond to the pints left standing and whose least significant bit corresponds to pin
0, e.g.0b1100000100for pins 2, 8 and 9.
You may assume input is sorted, if that helps you in any way.
Output
A single consistent value for Falsy test cases and anything else for Truthy test cases.
Test cases
Truthy
[0, 9]
[2, 8, 9]
[1, 5, 8]
[3, 5]
[3, 8]
[3, 9]
[6, 8]
[6, 9]
[3, 5, 8, 9]
[5, 6]
[0, 1, 5, 6, 7, 9]
[1, 2, 8, 9]
Falsy
[1, 2]
[7, 8, 9]
[1, 2, 5]
[2, 4]
[0, 1, 3, 6]
[2, 5, 9]
[6, 7]
[4, 7]
[4, 8]
[1, 4, 5, 7]
Bonus imaginary internet points
Bonus imaginary internet points if your algorithm works for any triangle number of pins, instead of just 10.
So far, only Grimmy's 05AB1E answer qualifies for the bonus internet points!
Standard loopholes are forbidden by default.
This is code-golf so shortest solution wins! If you enjoy the challenge, consider upvoting it... And happy golfing!
Somewhat related: Draw a bowling formation
– xnor – 2020-02-11T08:27:11.4971Can we assume at least 2 pins? – G B – 2020-02-11T10:10:13.510
1May we take the input as a single 10-bit integer? – Arnauld – 2020-02-11T12:06:02.093
A single consistent value for Falsy test cases and anything else for Truthy test cases. It seems like we have almost as many output rules as we have decision-problem challenges. :-/ – Arnauld – 2020-02-11T13:30:05.960
1@Noodle9 yes, the pin 2 was misplaced. Yes,
[1, 2, 8, 9]is a split spare and for the challenge, for a spare to be a split spare we only care about adjacency. We don't care about the headpin. – RGS – 2020-02-11T14:08:29.910@Arnauld yes you can take input as a 10 bit integer, where the set bits correspond to the pins that are standing, much like the input list has the indices of the pins left. Also, about the output rules: I thought this made sense! I fail to understand your objection :/ – RGS – 2020-02-11T14:14:06.457
1@RGS My initial version was outputting either false (Boolean value) or 0 (integer) for the falsy output. I had to fix it to always output false. – Arnauld – 2020-02-11T14:18:34.173
5A shame we couldn't make it a
code-bowlingcontest somehow! – JDL – 2020-02-11T16:51:29.753According to the linked page we only have a split if the head pin (0 here) has been knocked down, which would move a couple of the truthy tests to falsey ones - these would instead be "washouts". – Jonathan Allan – 2020-02-11T17:47:50.480
@JonathanAllan thanks for pointing the inconsistency out. I will edit the question to state clearly that we only care about adjacency for our definition of split spare. – RGS – 2020-02-11T17:52:03.790
@JDL we'll come up with something! – RGS – 2020-02-11T17:52:12.287
1Would he following input array be considered acceptable? For pins 2, 5, 6 being stuck up, [[0],[0,1],[0,0,1],[1,0,0,0]], split by rows, left-to-right? – Mathgeek – 2020-02-12T14:48:44.047
@Mathgeek The format
[[0], [0, 1], [0, 0, 1], [1, 0, 0, 0]]is acceptable, yes. – RGS – 2020-02-12T15:05:21.320