23
3
Output a random triple \$(x,y,z)\$ of real numbers such that
- \$x+y+z=\frac{3}{2}\$
- Each of \$x,y,z\$, taken alone, is uniformly distributed from \$0\$ to \$1\$.
Please explain in your answer what distribution your code produces and why it meets these conditions. In particular, please include a demonstration that with many samples produced by running your code many times, the distribution of each variable alone is approximately uniform.
Allowances for precision
Since computers can't produce actual real numbers, you can approximate them by outputting any of:
- Floats
- Decimals
- Rationals
I've tried to make the rules here as friendly as possible.
Your outputs need to be accurate within \$\pm 10^{-3}\$, that is 3 decimal digits. That means you can imagine that each real-number output from your true distribution has been fudged by at most \$\pm 10^{-3}\$ in any way. It's fine if this makes \$x+y+z\$ be a bit off from \$\frac{3}{2}\$.
You may output rationals as (numerator, denominator) pairs of integers or similar. You may also choose to output just one denominator that applies to all three values, that is, output \$a,b,c\$ and \$d\$ to represent \$\frac{a}{d},\frac{b}{d},\frac{c}{d}\$. Rationals don't have to be in reduced form.
Randomness
You can assume any standard PRNG is in fact random. For instance, if it outputs random floats from 0 to 1, you can assume these are uniformly random reals that are independent from each other, and not worry about any endpoint issues. It's also fine if your code fails in a probability-zero event.
To decide whether a pseudo-random source such as time or memory contents is sufficiently random, consider an empirical test where your code is run many times in sequence to check if the randomness varies sufficiently between runs. You may have these runs be done within your language such as in a loop, or by repeatedly calling the code from outside like with a shell command. You may not assume any intentional time delay or other actions taken between runs.
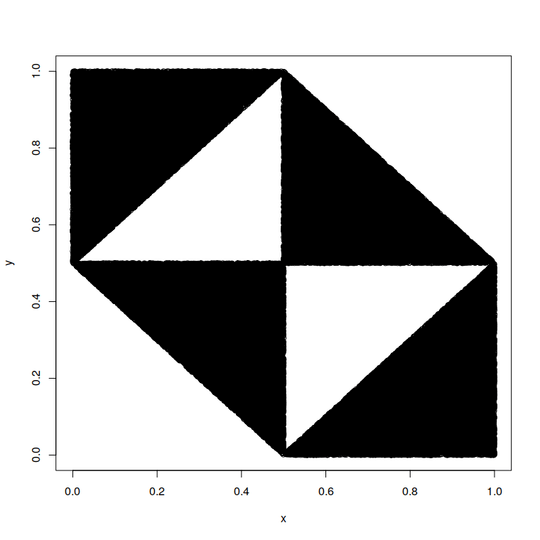
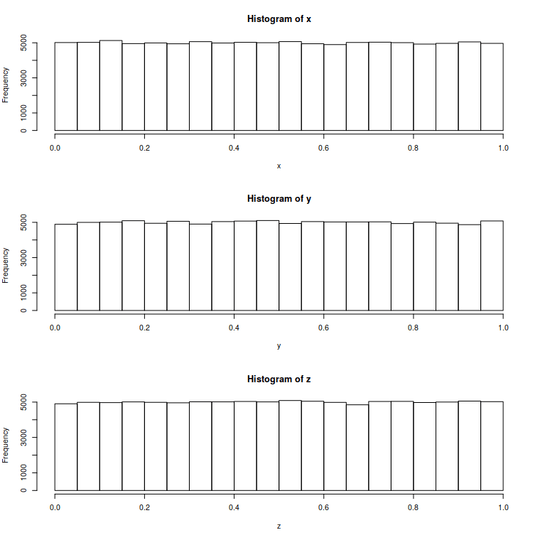
1Related, basically the same except that the distribution is $(-1,1)$ and the equation is $ x^2 + y^2 + z^2 = 1$ – Jo King – 2019-12-29T23:50:38.233
2@ChasBrown I think what Jo King is referring to is the interesting property of the uniform distribution on the sphere that each of its coordinates alone has the uniform distribution. – xnor – 2019-12-30T00:19:11.483
1
Perhaps more closely related?
– Giuseppe – 2019-12-30T01:00:08.1801can we output 3 ints between 0 and 1000 whose sum is 1500? – ngn – 2019-12-30T10:27:17.430
@ngn Yes, except you need to also need to output the number 1000 as per the rationals option with one denominator. – xnor – 2019-12-30T10:37:19.313
@xnor: In Re uniform points on a sphere: Well, I'll be darned - it is uniformly distributed on the interval for each axis! – Chas Brown – 2019-12-30T20:50:47.733
Is the range $(0,1)$ or are we also allowed to use a range $(0,1]$ instead (i.e. is
[1.000, 0.100, 0.400]a valid output)? – Kevin Cruijssen – 2020-01-03T08:22:32.9271@KevinCruijssen Any way of treating endpoints is fine. – xnor – 2020-01-03T08:27:22.600