Fractal Smoke Sequence

Question

Introduction

A229037 has a quite intriguing plot (at least for the first few terms):

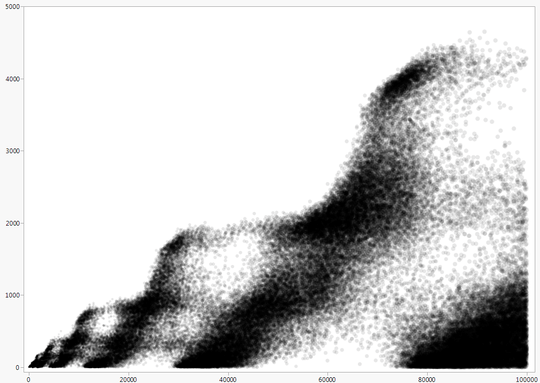
There is the conjecture, that it might indeed have some kind of fractal property.

How is this sequence constructed?

Define a(1) = 1, a(2) = 1 then for each n>2 find a minimal positive integer a(n) such that for every arithmetic 3 term sequence n,n+k,n+2k of indices, the corresponding values of the sequence a(n),a(n+k),a(n+2k) is not an arithmetic sequence.

Challenge

Given a positive integer n as an input, output the first n terms a(1), ... , a(n) of this sequence. (With any reasonable formatting. Possible leading/trainling characters/strings are irrelevant.)

There are snippets for generating this sequence available, but I think other approaches might be more golfable/more suitable for certain languages.

Please let us know how your progrm works. If you come a cross a particularly efficient algorithm you might want to mention that too, as it would allow to plot more terms of the sequence in shorter time.

First few test cases:

1, 1, 2, 1, 1, 2, 2, 4, 4, 1, 1, 2, 1, 1, 2, 2, 4, 4, 2, 4, 4, 5, 5, 8, 5, 5, 9, 1, 1, 2, 1, 1, 2, 2, 4, 4, 1, 1, 2, 1, 1, 2, 2, 4, 4, 2, 4, 4, 5, 5, 8, 5, 5, 9, 9, 4, 4, 5, 5, 10, 5, 5, 10, 2, 10, 13, 11, 10, 8, 11, 13, 10, 12, 10, 10, 12, 10, 11, 14, 20, 13

More testcases:

  a(100)  =   4
  a(500)  =   5
 a(1000)  =  55
 a(5000)  =  15
a(10000)  = 585

All terms up to n=100000 are available here: https://oeis.org/A229037/b229037.txt

Thanks @MartinBüttner for the help and encouragement.

Answer 1

Python 2, 95 bytes

l=[];n=input()
exec"a=min(set(range(n))-{2*b-c for b,c in zip(l,l[1::2])});print-~a;l=[a]+l;"*n

The main trick is in generating the numbers the new value must avoid. Keeping the reversed sequence so far in l, let's look at what elements might form a three-term arithmetic progression with the value we're about to add.

? 4 2 2 1 1 2 1 1   a b c
^ ^ ^               ? 4 2
^   ^   ^           ? 2 1
^     ^     ^       ? 2 2
^       ^       ^   ? 1 1

The other numbers are the paired members of l and every second element of l, so zip(l,l[1::2]). If this pair is (b,c) then the arithmetic progression (a,b,c) happens for a=2*b-c. After generating the set of a's to avoid, the code takes the minimum of the complement, prints it, and prepends it to the list. (Actually, the computation is done with numbers decreased by 1, and printed 1 higher, to let range(n) serve as a universe of candidates.)

Answer 2

Mathematica, 95 bytes

For[n_~s~k_=0;n=0,n<#,For[i=n,--i>0,s[2n-i,2f@n-f@i]=1];For[++n;i=1,n~s~i>0,++i];Print[f@n=i]]&

Certainly not the golfiest approach, but this is actually fairly efficient, compared to the algorithms I tried from the OEIS page.

As opposed to checking all the forbidden values for each s(n) when we get there I'm using a sieve-based approach. When we find a new value s(n) we check immediately which values this forbids for m > n. Then we just solve the s(n+1) by looking for the first value that wasn't forbidden.

This can be made even more efficient by changing the conditional --i>0 to 2n-#<=--i>0. In that case, we avoid checking forbidden values for n greater than the input.

For a somewhat more readable version, I started with this code, which stores the results up to max in a function f, and then golfed it to the above one-line pure function:

 max = 1000;
 ClearAll[sieve, f];
 sieve[n_, k_] = False;
 For[n = 0, n < max,
  temp = f[n];
  For[i = n - 1, i > 0 && 2 n - i <= max, --i,
   sieve[2 n - i, 2 temp - f[i]] = True;
   ];
  ++n;
  i = 1;
  While[sieve[n, i], ++i];
  f@n = i;
  ]

Answer 3

Brachylog, 33 31 bytes

;Ė{~b.hℕ₁≜∧.¬{ġh₃hᵐs₂ᶠ-ᵐ=}∧}ⁱ⁽↔

Try it online!

In case it matters: The 2-byte golf was possible thanks to a feature I requested after working on this challenge.

Explanation

We iteratively generate the sequence as a list in reverse order, e.g. [2,2,1,1,2,1,1], and reverse it at the end.

There are a couple of nested predicates here. Let's look at them from the inside out. The first one, ġh₃hᵐs₂ᶠ-ᵐ=, takes a candidate subsequence a(n),a(n-1),...,a(0) and determines whether a(n),a(n-k),a(n-2k) is an arithmetic sequence for some k.

ġ            Group the list into equal-length sublists (with the possible exception of
             the last sublist, which might be shorter)
 h₃          Get the first 3 sublists from that list
   hᵐ        and get the head of each of those 3 sublists
             We now have a list containing a(n),a(n-k),a(n-2k) for some k
     s₂ᶠ     Find all 2-element sublists of that list: [a(n),a(n-k)] and [a(n-k),a(n-2k)]
        -ᵐ   Find the difference of each pair
          =  Assert that the two pairwise differences are equal

For example, with input of [1,2,1,1,2,1,1]:

ġ has possible outputs of
    [[1],[2],[1],[1],[2],[1],[1]]
    [[1,2],[1,1],[2,1],[1]]
    [[1,2,1],[1,2,1],[1]]
    [[1,2,1,1],[2,1,1]]
    [[1,2,1,1,2],[1,1]]
    [[1,2,1,1,2,1],[1]]
    [[1,2,1,1,2,1,1]]
h₃ has possible outputs of
    [[1],[2],[1]]
    [[1,2],[1,1],[2,1]]
    [[1,2,1],[1,2,1],[1]]
hᵐ has possible outputs of
    [1,2,1]
    [1,1,2]
    [1,1,1]
s₂ᶠ has possible outputs of
    [[1,2],[2,1]]
    [[1,1],[1,2]]
    [[1,1],[1,1]]
-ᵐ has possible outputs of
    [-1,1]
    [0,-1]
    [0,0]
= is satisfied by the last of these, so the predicate succeeds.

The next predicate outwards, ~b.hℕ₁≜∧.¬{...}∧, inputs a subsequence a(n-1),a(n-2),...,a(0) and outputs the next bigger subsequence a(n),a(n-1),a(n-2),...,a(0).

~b.hℕ₁≜∧.¬{...}∧
~b.                 The input is the result of beheading the output; i.e., the output is
                    the input with some value prepended
  .h                The head of the output
    ℕ₁              is a natural number >= 1
      ≜             Force a choice as to which number (I'm not sure why this is necessary,
                    but the code doesn't work without it)
        ∧           Also,
         .          the output
          ¬{...}    does not satisfy the nested predicate (see above)
                    I.e. there is no k such that a(n),a(n-k),a(n-2k) is an arithmetic sequence
                ∧   Break unification with the output

Finally, the main predicate ;Ė{...}ⁱ⁽↔ takes an input number and outputs that many terms of the sequence.

;Ė{...}ⁱ⁽↔
;           Pair the input number with
 Ė          the empty list
  {...}ⁱ⁽   Using the first element of the pair as the iteration count and the second
            element as the initial value, iterate the nested predicate (see above)
         ↔  Reverse, putting the sequence in the proper order

Answer 4

Ruby, 71 bytes

->n,*a{a.fill(0,n){|s|([*1..n]-(1..s/2).map{|o|2*a[s-o]-a[s-2*o]})[0]}}

Try it online!

Generates all forbidden values, then takes the complement of that array in (1..n) and takes the first value of the result. That means I am assuming that a[n] <= n for all n, which is easily proven using induction (if the first n/2 terms are all less than n/2, then there can't be an arithmetic progression leading to n).

The syntactic trick here is also mildly interesting: *a is used to initialize an array of additional arguments (which would be ignored if we passed any), and then a.fill mutates the argument array and implicitly returns it.

Answer 5

APL (Dyalog Extended), 37 bytes^SBCS

Many thanks to Adám for his help in writing and golfing this answer in The APL Orchard, a great place to learn the APL language. Try it online!

Edit: -6 bytes thanks to Adám

⌽{⍵,⍨⊃(⍳1+≢⍵)~-¯2⊥⍵[2×⍀⍥⍳⌊2÷⍨≢⍵]}⍣⎕,⍬

Explanation

{⍵,⍨⊃(⍳1+≢⍵)~-¯2⊥⍵[2×⍀⍥⍳⌊2÷⍨≢⍵]}  ⍵ is our right argument, the sequence S

                        ⌊2÷⍨≢⍵    We start by calculating X = ⌊len(S)÷2⌋
                       ⍳          Get a range [1, X]
                   2×⍀⍥           With that we can get S[:X] and S[:X×2:2]
                                  or S up to halfway and every 2nd element of S
             -¯2⊥⍵[           ]   And with that we can get 2*S[:X] - S[:X×2:2]
                                  Which is C=2*B-A of a progression A B C
     (⍳1+≢⍵)~                     We remove these Cs from our possible a(n)s
                                  I use range [1, len(S)+1]
    ⊃                             Get the first result, which is the minimum
 ⍵,⍨                              And then prepend that to S


⌽{...}⍣⎕,⍬

 {...}⍣⎕    We iterate an "input" ⎕ times
        ,⍬  with an empty list ⍬ as the initial S
⌽           and reversing S at the end as we have built it backwards

APL (Dyalog Unicode), 43 39 38 bytes^SBCS

Here is a faster but less golfy solution that can calculate ⍺(10000) in a few seconds.

⌽{⍵,⍨⊃(⍳1+≢⍵)~-⌿⍵[1 2 1∘.×⍳⌊2÷⍨≢⍵]}⍣⎕,⍬

Try it online!

Answer 6

Haskell, 90, 89, 84, 83 bytes

Can probably be golfed more, but this is still a decent first attempt:

a n|n<1=0|n<3=1|1<2=[x|x<-[1..],and[x/=2*a(n-k)-a(n-k-k)||a(n-k-k)<1|k<-[1..n]]]!!0

Ungolfed:

a n | n<1        = 0 
    | n<3        = 1
    | otherwise  = head (goods n)

goods n = [x | x <- [1..], isGood x n]

isGood x n = and [ x - a(n-k) /= a(n-k) - a(n-k-k) || a(n-k-k) == 0 | k <- [1..n] ]

This is a simple implementation which returns '0' for out of bounds. Then, for each possible value, it checks that for all k <= n and in bounds, [x, a(x-k), a(x-2k)] is not an arithmetic sequence.

Upper bound on time complexity (using the fact from the OEIS page that a(n) <= (n+1)/2:

t n <= sum[ sum[2*t(n-k) + 2*t(n-k-k) | k <- [1..n]] | x <- [1..(n+1)/2]]
    <= sum[ sum[4*t(n-1)              | k <- [1..n]] | x <- [1..(n+1)/2]]
    <= sum[     4*t(n-1)*n                         ] | x <- [1..(n+1)/2]]
    <=          4*t(n-1)*n*(n+1)/2
    ->
O(t(n)) == O(2^(n-2) * n! * (n+1)!)

I'm not sure how good this bound is because calculating the first 1k values of 't' and using a linear model on the logs of the values gave appx. O(22^n), with p-value < 10^(-1291), in case it matters.

On an implementation level, compiling with '-O2', it took ~35 min to calculate the first 20 values.

Answer 7

Jelly, 24 19 bytes

This is my first Jelly answer in quite a while. Glad to be back.

This is a port of my APL answer which itself is an adaptation of many of the algorithms used here. The main difference is that this is 0-indexed.

Edit: -5 bytes thanks to Jonathan Allan.

Try it online!

Ḋm2ɓṁḤ_
ŻJḟÇṂ;
1Ç¡U

Explanation

Ḋm2ɓṁḤ_  First link. Takes our current sequence S as our left argument.

         We are trying to calculate, of an arithmetic progression A B C, 
           the C using the formula, C = 2*B - A
Ḋ        Remove the first element of S.
 m2      Get every element at indices 0, 2, 4, ...
           This is equivalent to getting every second element of S, a list of As.
   ɓ     Starts a dyad with reversed arguments.
           The arguments here are S and As.
    ṁ    This molds S in the shape of As, giving us a list of Bs.
     Ḥ   We double the Bs.
      _  And subtract As from 2 * Bs.

ŻJḟÇṂ;  Second link. Takes S as our left argument.

Ż       Append a 0 to S.
 J      Range [1, len(z)]. This gets range [1, len(S) + 1].
  ḟÇ    Filter out the results of the previous link, our Cs.
    Ṃ   Take the minimum of Cs.
     ;  And concatenate it with the rest of the sequence so far.

1Ç¡U  Third link. Where we feed our input, n.

1     A list with the element 1.
 Ç¡   Run the previous link n times.
   U  Reverse everything at the end.

Answer 8

MATLAB, 156 147 bytes

I've finally gotten to golf this down a bit:

N=input('');s=[0;0];for n=1:N,x=s(n,~~s(n,:));try,a(n)=find(~ismember(1:max(x)+1,x),1);catch,a(n)=1;end,s(n+1:2*n-1,end+1)=2*a(n)-a(n-1:-1:1);end,a

Ungolfed:

N=input('');                                   % read N from stdin

s=[0;0];
for n=1:N,
    x=s(n,~~s(n,:));                           % x=nonzeros(s(n,:));
    try,
        a(n)=find(~ismember(1:max(x)+1,x),1);  % smallest OK number
    catch,
        a(n)=1;                                % case of blank page for n
    end,

    s(n+1:2*n-1,end+1)=2*a(n)-a(n-1:-1:1);     % determined new forbidden values
end,
a                                              % print ans=...

Input is read from STDIN, and printing is done automatically with ans= and stuff appended. I hope this qualifies as "reasonable" output.

This is also a sieve-based solution: the variable s(i,:) keeps track of those sequence values which are forbidden for a(i). The try-catch block is needed to treat the case of an empty (meaning full zero) s matrix: in this case the lowest value of 1 is already allowed.

However, the memory need (or runtime?) gets pretty messy above N=2000. So here's a non-competing, more efficient solution:

%pre-alloc
s = zeros([N,fix(N*0.07+20)]); %strict upper bound, needs adjusting later
i = zeros(1,N);

a = 1;
for n = 2:N,
    x = s(n,1:i(n));
    if isempty(x),
        a(n) = 1;
    else
        a(n) = find(~ismember(1:max(x)+1,x),1);
    end,

    j = n+1:min(2*n-1,N);
    i(j) = i(j)+1;
    s(N,max(i(j))) = 0;   %adjust matrix size if necessary
    b = a(n-1:-1:1);
    s(sub2ind([N,size(s,2)+1],j,i(j))) = 2*a(n)-b(1:length(j));
end

In this implementation the s matrix again contains forbidden values, but in a well-ordered way, without any zero blocks (which are present in the competing version). The index vector i keeps track of the number of forbidden vectors in s. At first sight cells would be great to keep track of the information stored in s, but those would be slow, and we couldn't index a bunch of them at the same time.

One nasty feature of MATLAB is that while you can say M(1,end+1)=3; and automatically expand a matrix, you can't do the same with linear indexing. It sort of makes sense (how should MATLAB know the resulting array size, in the framework of which it should interpret the linear indices?), but it still surprised me. This is the reason for the superfluous line s(N,max(i(j))) = 0;: this will expand the s matrix for us whenever necessary. The starting size guess N*0.07+20 comes from a linear fit to the first few elements, by the way.

In order to test runtime, I also checked a slightly modified version of the code, where I initialized the s matrix to have size N/2. For the first 1e5 elements this seems to be a very generous guess, so I removed the expansion step of s mentioned in the previous paragraph. These together imply that the code will be faster, but also less robust at very high N (since I don't know how the series looks like there).

So here are a few runtimes, comparing

• v1: the competing golfed version,
• v2: the low-starting-size, fool-proof version and
• v3: the generous-starting-size, might-fail-for-large-N version.

I measured these on R2012b, taking the best of 5 runs inside a named function definition with tic/toc.

1. N=100:
   • v1: 0.011342 s
   • v2: 0.015218 s
   • v3: 0.015076 s
2. N=500:
   • v1: 0.101647 s
   • v2: 0.085277 s
   • v3: 0.081606 s
3. N=1000:
   • v1: 0.641910 s
   • v2: 0.187911 s
   • v3: 0.183565 s
4. N=2000:
   • v1: 5.010327 s
   • v2: 0.452892 s
   • v3: 0.430547 s
5. N=5000:
   • v1: N/A (didn't wait)
   • v2: 2.021213 s
   • v3: 1.572958 s
6. N=10000:
   • v1: N/A
   • v2: 6.248483 s
   • v3: 5.812838 s

It would seem that the v3 version is significantly, but not overwhelmingly faster. I don't know whether an element of uncertainty (for very large N) is worth the minor increase in runtime.

Answer 9

ES6, 114 bytes

n=>[...r=Array(n)].map((x,i,s)=>{for(y=1;x&&x[y];y++);r[i]=y;for(j=i;++j<n;s[j][y+y-r[i+i-j]]=1)s[j]=s[j]||[]}&&r

Returns an array of the first n elements of the sequence, so the indices are 1 off the ungolfed version below. I used the sieve approach. This version slows down after about n=2000; a previous version avoided reading off the beginning of the array which meant it didn't slow down until about n=2500. An older version used the sieve array as a list of forbidden values rather than a boolean array of which values were forbidden; this could get to about n=5000 without breaking sweat. My original version tried to use bitmasks but that turned out to be unhelpful (and was also far too long at 198 bytes).

The not quite so slow version ungolfed:

function smoke(n) {
    result = [];
    sieve = [];
    for (i = 1; i <= n; i++) {
        value = 1;
        if (sieve[i]) {
            while (sieve[i][value]) {
                value++;
            }
        }
        result[i] = value;
        for (j = 1; j < i && i + j <= n; j++) {
            if (!sieve[i + j]) sieve[i + j] = [];
            sieve[i + j][value + value - result[i - j]] = true;
        }
    }
    return result;
}