77
11
Your goal is to print (to the standard output) the largest number possible, using just ten characters of code.
- You may use any features of your language, except built-in exponentiation functions.
- Similarly, you may not use scientific notation to enter a number. (Thus, no
9e+99.)
- Similarly, you may not use scientific notation to enter a number. (Thus, no
- The program must print the number without any input from the user. Similarly, no reading from other files, or from the Web, and so on.
- Your program must calculate a single number and print it. You can not print a string, nor can you print the same digit thousands of times.
- You may exclude from the 10-character limit any code necessary to print anything. For example, in Python 2 which uses the
print xsyntax, you can use up to 16 characters for your program. - The program must actually succeed in the output. If it takes longer than an hour to run on the fastest computer in the world, it's invalid.
- The output may be in any format (so you can print
999,5e+100, etc.) - Infinity is an abstract concept, not a number. So it's not a valid output.
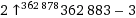
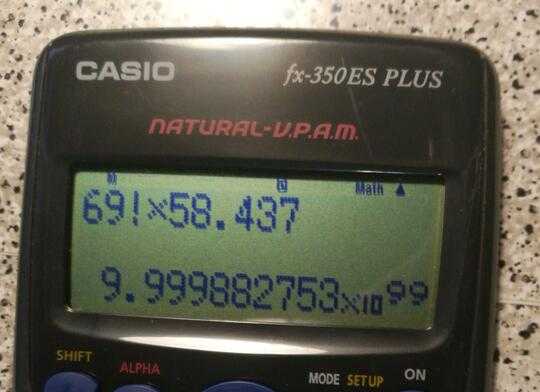

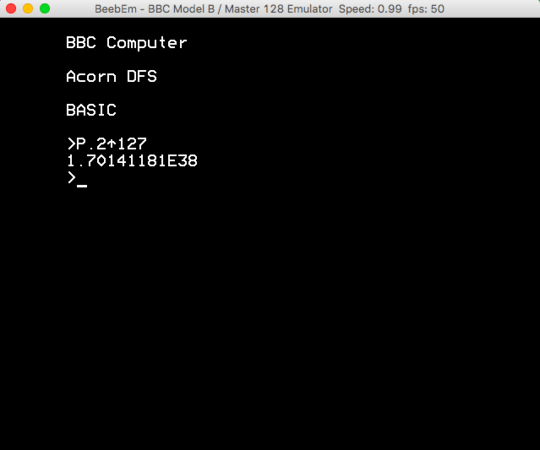
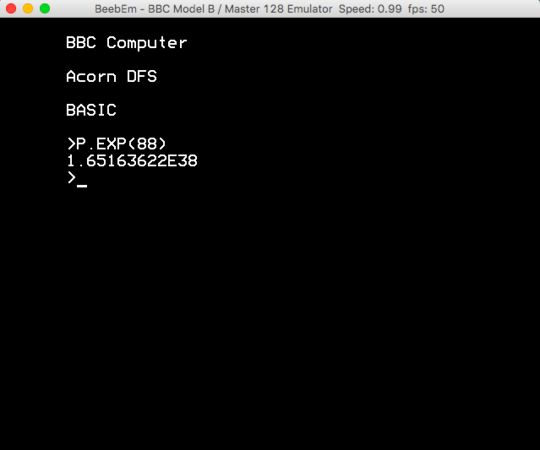
6Exponentiation functions are not allowed, but ackermann function is allowed? That seems really arbitrary. It remains unclear why a symbolic manipulation is considered "calculating" the number. – Reinstate Monica – 2015-07-07T13:12:15.070
1It would be fun to see this for each of 1..10 bytes. – None – 2016-05-06T15:41:25.330
what about Aceto, where you can do: 9pppppppppppppppp (9 pushes 9 on the stack, and p prints out 9('0'*p)s – FantaC – 2017-11-16T19:37:47.527
@Dennis It's not an estimate, it's an exact result, but it's a trivial conversion from Ackermann to arrow notation, like taking a square root and turning it into a negative exponent. Literally, ack(m,n) = 2 ↑ ⁽ᵐ⁻²⁾ (n+3) - 3 – user0721090601 – 2019-07-28T22:49:35.470
4
Did you look at these two?
http://codegolf.stackexchange.com/questions/185/print-largest-integer-you-can-with-the-fewest-characters
http://codegolf.stackexchange.com/questions/18028/largest-number-printable
21What do you exactly mean by "calculate". Also,
If it takes longer than an hour to run on any computer in the world, it's invalid.is not objective. I could (theoretically) manufacture a computer that takes an hour to change one T-state – user80551 – 2014-06-13T13:37:26.763@user80551 I clarified what I meant by "any". – Ypnypn – 2014-06-13T13:38:04.503
@MadTux None of the top answers on those questions are valid here, since they either take millions of years to run, or are way longer than 10 characters. – Ypnypn – 2014-06-13T13:39:29.173
1Do imports count to the 10 char limit too? – chill0r – 2014-06-13T14:57:36.023
I've voted to close as "Too broad", for reasons which will be obvious if you read the answers to the first question linked by MadTux above. – Peter Taylor – 2014-06-13T15:11:32.437
2@PeterTaylor Well, it is getting all sorts of entertaining answers, and the 10-character limit makes things interesting, so I'm beginning to like it. – MadTux – 2014-06-13T15:31:14.107
4Does bit-shift count as an exponentiation operator since it is equivalent to
* 2^x? – Claudiu – 2014-06-13T16:08:25.053@PeterTaylor: This is far less broad than that, though. There is actually a scoring criterion (the number), a program criterion (<= 10 chars), and a time limit (< 1 hour running time) – Claudiu – 2014-06-13T16:59:25.717
1@Claudiu: "the output may be in any format" – Peter Taylor – 2014-06-13T17:18:45.057
14The fact that the time limit depends on the performance of the fastest computer in the world makes it impossible for us to determine the set of valid answers... I don't really like that – David Z – 2014-06-13T19:45:09.803
4@DavidZ: True. I'd like to see it changed to "1 hour on X computer", and also clarify the rules as to bit-shift, and whether other large built-in functions (e.g. ack in Wolfram) are allowed. I guess not the best question, but I enjoyed playing to the spirit of the rules – Claudiu – 2014-06-13T20:47:52.500
3As I see it, the problem with
ackas used in the current Wolfram answers is that it doesn't calculate the result, it just estimates it. – Dennis – 2014-06-14T01:14:44.753Are importing the libraries is counted as a code? – kenorb – 2014-06-14T09:37:10.183
So you want the longest number possible in 10 bytes but not the largest number possible? – Anonymous Penguin – 2014-06-14T22:04:03.730
I don't like the rules. I could have posted this
last [1..]. It extracts the last element of an infinite list. – gxtaillon – 2014-06-15T13:44:21.010@Ypnypn One of the rules currently says, "you may not use scientific notation to enter a number". The rules appear to barely leave open the possibility for our code to use scientific notation inside a string literal. Is that so? I suppose
eval("9e9")still isn't quite as large as9999999999. – Keen – 2014-06-20T20:33:55.403