14
3
The dihedral group \$D_4\$ is the symmetry group of the square, that is the moves that transform a square to itself via rotations and reflections. It consists of 8 elements: rotations by 0, 90, 180, and 270 degrees, and reflections across the horizontal, vertical, and two diagonal axes.
The images are all from this lovely page by Larry Riddle.
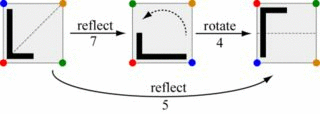
This challenge is about composing these moves: given two moves, output the move that's equivalent to doing them one after another. For instance, doing move 7 followed by move 4 is the same as doing move 5.
Note that switching the order to move 4 then move 7 produces move 6 instead.
The results are tabulated below; this is the Cayley table of the group \$D_4\$. So for example, inputs \$7, 4\$ should produce output \$5\$.
\begin{array}{*{20}{c}} {} & {\begin{array}{*{20}{c}} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ \end{array} } \\ {\begin{array}{*{20}{c}} 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \\ 7 \\ 8 \\ \end{array} } & {\boxed{\begin{array}{*{20}{c}} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 \\ 2 & 3 & 4 & 1 & 8 & 7 & 5 & 6\\ 3 & 4 & 1 & 2 & 6 & 5 & 8 & 7\\ 4 & 1 & 2 & 3 & 7 & 8 & 6 & 5\\ 5 & 7 & 6 & 8 & 1 & 3 & 2 & 4\\ 6 & 8 & 5 & 7 & 3 & 1 & 4 & 2\\ 7 & 6 & 8 & 5 & 4 & 2 & 1 & 3\\ 8 & 5 & 7 & 6 & 2 & 4 & 3 & 1\\ \end{array} }} \\ \end{array}
Challenge
Your goal is to implement this operation in as few bytes as possible, but in addition to the code, you also choose the labels that represent the moves 1 through 8. The labels must be 8 distinct numbers from 0 to 255, or the 8 one-byte characters their code points represent.
Your code will be given two of the labels from the 8 you've chosen, and must output the label that corresponds to their composition in the dihedral group \$D_4\$.
Example
Say you've chosen the characters C, O, M, P, U, T, E, R for moves 1 through 8 respectively. Then, your code should implement this table.
\begin{array}{*{20}{c}} {} & {\begin{array}{*{20}{c}} \, C \, & \, O \, & M \, & P \, & U \, & \, T \, & \, E \, & R \, \\ \end{array} } \\ {\begin{array}{*{20}{c}} C \\ O \\ M \\ P \\ U \\ T \\ E \\ R \\ \end{array} } & {\boxed{\begin{array}{*{20}{c}} C & O & M & P & U & T & E & R \\ O & M & P & C & R & E & U & T\\ M & P & C & O & T & U & R & E\\ P & C & O & M & E & R & T & U\\ U & E & T & R & C & M & O & P\\ T & R & U & E & M & C & P & O\\ E & T & R & U & P & O & C & M\\ R & U & E & T & O & P & M & C\\ \end{array} }} \\ \end{array}
Given inputs E and P, you should output U. Your inputs will always be two of the letters C, O, M, P, U, T, E, R, and your output should always be one of these letters.
Text table for copying
1 2 3 4 5 6 7 8
2 3 4 1 8 7 5 6
3 4 1 2 6 5 8 7
4 1 2 3 7 8 6 5
5 7 6 8 1 3 2 4
6 8 5 7 3 1 4 2
7 6 8 5 4 2 1 3
8 5 7 6 2 4 3 1

Your choice of labels doesn't count against your code length.mind elaborating? As it stands, I can hardcode the matrix into my code and claim it doesn't count against my score. – Benjamin Urquhart – 2019-05-04T02:04:33.6072@BenjaminUrquhart I was trying to say the length of your code is just the length of your code, and say, choosing multidigit labels doesn't cost anything extra. Looks like that line is more confusing that helpful, so I'll remove it. – xnor – 2019-05-04T02:06:06.670