20
1
First, let's talk about Beatty sequences. Given a positive irrational number r, we can construct an infinite sequence by multiplying the positive integers to r in order and taking the floor of each resulting calculation. For example,
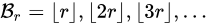
If r > 1, we have a special condition. We can form another irrational number s as s = r / (r - 1). This can then generate its own Beatty sequence, Bs. The neat trick is that Br and Bs are complementary, meaning that every positive integer is in exactly one of the two sequences.
If we set r = ϕ, the golden ratio, then we get s = r + 1, and two special sequences. The lower Wythoff sequence for r:
1, 3, 4, 6, 8, 9, 11, 12, 14, 16, 17, 19, 21, 22, 24, 25, 27, 29, ...
and the upper Wythoff sequence for s:
2, 5, 7, 10, 13, 15, 18, 20, 23, 26, 28, 31, 34, 36, 39, 41, 44, 47, ...
These are sequences A000201 and A001950 on OEIS, respectively.
The Challenge
Given a positive input integer 1 <= n <= 1000, output one of two distinct values indicating whether the input is in the lower Wythoff sequence or the upper sequence. The output values could be -1 and 1, true and false, upper and lower, etc.
Although your submitted algorithm must theoretically work for all inputs, in practice it only has to work with the first 1000 input numbers.
I/O and Rules
- The input and output can be given by any convenient method.
- The input and output can be assumed to fit in your language's native number type.
- Either a full program or a function are acceptable. If a function, you can return the output rather than printing it.
- Standard loopholes are forbidden.
- This is code-golf so all usual golfing rules apply, and the shortest code (in bytes) wins.
1It's basically "golf the lower Wythoff sequence" because the upper Wythoff sequence requires 1 more op than the lower one (squaring phi). – Magic Octopus Urn – 2018-06-15T13:28:13.033