The "prime ant" is an obstinate animal that navigates the integers and divides them until there are only primes left!

Initially, we have an infinite array A containing all the integers >= 2 : [2,3,4,5,6,.. ]

Let p be the position of the ant on the array. Initially, p = 0 (array is 0-indexed)

Each turn, the ant will move as follows:

if A[p] is prime, the ant moves to the next position : p ← p+1
else, if A[p] is a composite number, let q be its smaller divisor > 1. We divide A[p] by q, and we add q to A[p-1]. The ant moves to the previous position: p ← p-1

Here are the first moves for the ant:

 2  3  4  5  6  7  8  9  ... 
 ^
 2  3  4  5  6  7  8  9  ... 
    ^
 2  3  4  5  6  7  8  9  ... 
       ^
 2  5  2  5  6  7  8  9  ... 
    ^
 2  5  2  5  6  7  8  9  ... 
       ^
 2  5  2  5  6  7  8  9  ... 
          ^
 2  5  2  5  6  7  8  9  ... 
             ^
 2  5  2  7  3  7  8  9  ... 
          ^

Your program should output the ant's position after n moves. (you can assume n <= 10000)

Test cases:

0 => 0
10 => 6
47 => 9
4734 => 274
10000 => 512

Edit. you can also use 1-indexed lists, it's acceptable to display the results 1, 7, 10, 275, 513 for the above test case.

This is code-golf, so the code with the shortest code in bytes wins.

Arnaud

Posted 2017-10-09T02:28:45.480

Reputation: 8 231

32I honestly thought there was an ant on my screen when I saw this in the Hot Network Questions. – Kodos Johnson – 2017-10-09T06:09:20.927

14I wonder whether the sequence is well-defined for arbitrarily large n (or whether the composite case could ever push the ant to the left of the initial 2). – Martin Ender – 2017-10-09T06:59:49.310

Can we use 1-indexing for the array instead? – Tom Carpenter – 2017-10-09T09:12:13.280

@Tom Yes, no problem, as long as your program returns the correct results. – Arnaud – 2017-10-09T09:17:23.780

1@SuperChafouin so outputs of for the test cases can be: 1,7,10,275,513 if 1-indexing stated? Or would they still need to match your outputs. – Tom Carpenter – 2017-10-09T09:22:30.923

@SuperChafouin if we're using 1indexed array, is a 1-indexed result "correct"? – kamoroso94 – 2017-10-09T10:25:11.913

It's OK for me. I edit the question to allow 0-indexation or 1-indexation. – Arnaud – 2017-10-09T10:32:40.280

12@MartinEnder Another open question is whether a prime > 7 can eventually be left behind for good. – Arnauld – 2017-10-09T10:39:15.740

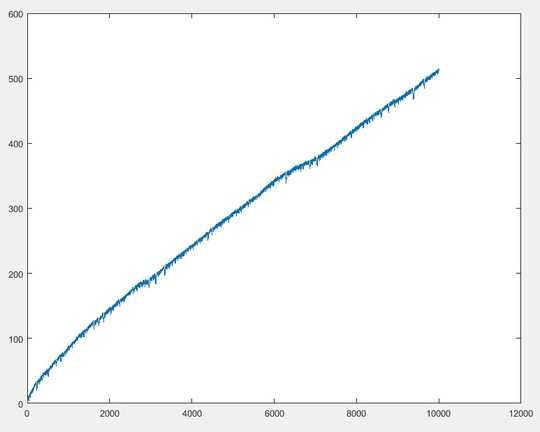
@Arnauld I'm curious how the ant's position grows with respect to the number of moves. My guess is logarithmic. – kamoroso94 – 2017-10-09T12:58:03.850

@kamoroso94 It's probably somehow related to ω(n) and/or Ω(n). If p is the position and n is the number of moves, then p seems to be in the order of magnitude of n.log(n)/log(log(n)). But that's a complete guess...

– Arnauld – 2017-10-09T16:05:00.563

I have the Android widget for stack exchange...I thought there was a bug on my screen. – Evorlor – 2017-10-09T21:33:30.073

1@Arnauld Yeah, we can conjecture that for any given position P≥0 there is an N≥0 (depending on P) such that if the number n of moves is greater than N, then the position f(n) of the ant will always be greater than P, and the array entries with indices small than P will all be one-digit prime numbers (i.e. belong to { 2, 3, 5, 7 }). – Jeppe Stig Nielsen – 2017-10-10T14:23:45.393

Looks oddly related to this mathematical sequence, wonder whether we could alter the projection to stop it diverging later on in the sequence: M(0)=0; M(n+1)=M(n).f(M(n), n).f(M(n), n+1).d(M(n), n); -f(m, n)

– Alexander Craggs – 2017-10-10T15:18:06.923

@KodosJohnson, gotta love outdoor computing! – NH. – 2017-10-10T19:47:43.880

2@Arnauld Out as far as move n = 1,000,000,000 (where p = 17156661), the relationship between n and p is very close to p = n/(ln(n)*ln(ln(n))) . – Penguino – 2017-10-12T03:17:53.397

I added this sequence to the On-Line Encylopedia of Integer Sequences as sequence A293689. The graph is worth looking at.

– Peter Kagey – 2017-10-19T04:39:08.013

Answers

Alice, 45 bytes

/o
\i@/.&wqh!]k.&[&w;;?c]dt.n$k&;[.?~:![?+!kq

Try it online!

Mostly straightforward implementation.

Looping n times in Alice is typically done by pushing a return address n-1 times, then returning at the end of each iteration with k. The last time through the loop, the k instruction has nowhere to return to, and execution proceeds forward.

This program uses the same k instruction to stop early when the number is prime. As a result, the final iteration will always move the ant left. To compensate for this bug, we do n+1 iterations on a 1-indexed array, which gives exactly the result we want (and gives the case n=0 for free).

Nitrodon

Posted 2017-10-09T02:28:45.480

Reputation: 9 181

Octave, 109 103 101 94 bytes

function i=a(n)i=1;for l=z=2:n+1
if nnz(q=factor(z(i)))>1
z(i--)/=p=q(1);z(i--)+=p;end
i++;end

Try it online!

This code will output the position in 1-indexing, so outputs for test cases are:

0 => 1
10 => 7
47 => 10
4734 => 275
10000 => 513

This version uses some Octave optimisations so isn't compatible with MATLAB. The code below is a MATLAB compatible version.

MATLAB, 130 123 118 117 bytes

function i=a(n)
z=2:n+1;i=1;for l=z
q=factor(z(i));if nnz(q)>1
z(i)=z(i)/q(1);i=i-1;z(i)=z(i)+q(1);else
i=i+1;end
end

Uses 1-indexing as with the Octave version. I've tested it against all test cases in MATLAB. As an example the output at 100000 is 3675 (one-indexing).

An commented version of the above code:

function i=a(n)
    z=2:n+1;                %Create our field of numbers
    i=1;                    %Start of at index of 1 (MATLAB uses 1-indexing)
    for l=1:n               %For the required number of iterations
        q=factor(z(i));     %Calculate the prime factors of the current element
        if nnz(q)>1         %If there are more than one, then not prime
            z(i)=z(i)/q(1); %So divide current by the minimum
            i=i-1;          %Move back a step
            z(i)=z(i)+q(1); %And add on the minimum to the previous.
        else
            i=i+1;          %Otherwise we move to the next step
        end
    end

As a matter of interest, this is the ants positions vs number of iterations for the first 10000 values of n.

Seems likely that the Ant will probably tend to infinity, but who knows, looks can be deceiving.

MATLAB: Saved 6 bytes with for instead of while and removing brackets from if - Thanks @Giuseppe
MATLAB: Save 2 bytes - Thanks @Sanchises
Octave: Save 10 bytes by using Octave \= and += operations - Thanks @Giuseppe
Octave: Save 2 bytes with i++ and i-- - Thanks @LuisMendo
Octave: Save 7 bytes - Thanks @Sanchises

Tom Carpenter

Posted 2017-10-09T02:28:45.480

Reputation: 3 990

To get it to work on TIO, I think you need an end to match the function signature – Giuseppe – 2017-10-09T11:12:21.200

@Giuseppe Ah, ok. In MATLAB the trailing end is optional. – Tom Carpenter – 2017-10-09T11:18:09.853

you can make anonymous function by using @(n) at the start instead of using function i=a(n) – Michthan – 2017-10-09T11:39:18.937

@Michthan can't do that in MATLAB. I don't think it is possible in Octave either as it has loops? – Tom Carpenter – 2017-10-09T11:44:35.413

1The trailing end is optional in Octave too. Here it is only needed because you have code after the function – Luis Mendo – 2017-10-09T11:52:33.850

@TomCarpenter https://www.gnu.org/software/octave/doc/v4.0.3/Anonymous-Functions.html#Anonymous-Functions That's where I found my information about anonymous functions;

– Michthan – 2017-10-09T11:57:28.213

In Octave we get +=, -=, /= so this is much shorter in Octave but then it won't work in MATLAB. But if(nnz(q)>1) should be if nnz(q)>1 for -1 byte. – Giuseppe – 2017-10-09T13:44:06.330

@Giuseppe cool, should of spotted those brackets. I like learning new optimisations like the += etc, don't know why MATLAB doesn't have them. Saved a couple more as well by using for l=z instead of for l=1:n. – Tom Carpenter – 2017-10-09T14:39:53.053

@LuisMendo that's what I did as well (put the end in the footer on TIO). – Tom Carpenter – 2017-10-09T16:12:19.863

Actually, I got it down to 91 bytes: Try it online!. Do you mind if I post this as my own answer? (the algorithm is the same, but the implementation is quite different)

– Sanchises – 2017-10-20T10:09:46.810

@Sanchises might as well at this point, lol. – Tom Carpenter – 2017-10-20T10:10:26.677

Actually, I don't feel like making a whole answer with explanation, so you may post my 90 bytes version, Try it online!, if you like :)

– Sanchises – 2017-10-20T11:34:31.543

Python 2, 120 bytes

p=0
A=range(2,input()+2)
for _ in A:
 for q in range(2,A[p]):
	if A[p]%q<1:A[p]/=q;p-=1;A[p]+=q;break
 else:p+=1
print p

Try it online!

Ah, the rare for–else loop! The else clause only executes if the for body is not exited via break. In our case, this means we checked all qs and found none of them to divide p.

Lynn

Posted 2017-10-09T02:28:45.480

Reputation: 55 648

JavaScript (ES6), 91 bytes

f=(n,a=[p=0])=>n--?f(n,a,(P=n=>++x<n?n%x?P(n):a[a[p]/=x,--p]+=x:p++)(a[p]=a[p]||p+2,x=1)):p

Demo

NB: You may have to increase the default stack size of your engine to have it pass all test cases.

Try it online!

Arnauld

Posted 2017-10-09T02:28:45.480

Reputation: 111 334

Haskell, 108 106 94 bytes

([0]#[2..]!!)
(a:b)#(p:q)=length b:([b#(a+d:div p d:q)|d<-[2..p-1],mod p d<1]++[(p:a:b)#q])!!0

Try it online! Example usage: ([0]#[2..]!!) 10 yields 6 (0-indexed).

The function # operates on two list, the reversed front of the array [p-1, p-2, ..., 1] and the infinite rest of the array [p, p+1, p+2, ...]. It constructs an infinite list of positions, from which the nth position is returned given an input n.

The pattern ((a:b)#(p:q)) binds p to the value of the current position of the ant and a to the value a the previous position. b is the prefix of the array from position 1 to p-2 and q the infinite rest starting from position p+1.

We construct a list of recursive calls in the following way: We look at each divisor d of p (which is larger than one and smaller than p) in ascending order and add b#(a+d:div p d:q) for each of them, that is the current value p is divided by d and the ant moves one step to the left where d is added to a. Then we append (p:a:b)#q to the end of this list, which indicates the ant moving one step to the right.

We then take the first of those recursive calls from the list and prepend the current position, which coincides with the length of the prefix list b. Because the divisors are in ascending order, picking the first from the list of recursive calls ensures we use the smallest one. Additionally, because (p:a:b)#q is added to the end of the list, it is only selected if there are no divisors and p is thus prime.

Edits:
-2 bytes by switching the list of functions from descending to ascending order.
-12 bytes thanks to Zgarb's idea to index into an infinite list instead handling a counter, and by switching to 0-indexing.

Laikoni

Posted 2017-10-09T02:28:45.480

Reputation: 23 676

296 bytes by building an infinite list and indexing, instead of carrying around the counter. – Zgarb – 2017-10-09T15:17:48.403

1@Zgarb Thanks a lot! It's even only 94 bytes when switching to 0-indexing. – Laikoni – 2017-10-10T06:30:07.240

TI-BASIC, 108 103 102 98 bytes

Input and output are stored in Ans. Output is 1-indexed.

Ans→N
seq(X,X,2,9³→A
1→P
For(I,1,N
1→X:∟A(P→V
For(F,2,√(V
If X and not(fPart(V/F:Then
DelVar XV/F→∟A(P
P-1→P
F+∟A(P→∟A(P
End
End
P+X→P
End

kamoroso94

Posted 2017-10-09T02:28:45.480

Reputation: 739

You can take a byte off of fPart(∟A(P)/F: with fPart(F¹∟A(P:. Same thing in the next line. – Scott Milner – 2017-10-11T00:51:02.717

@ScottMilner That doesn't always work. not(fPart(7⁻¹7 is 0 but not(fPart(7/7 is 1. – kamoroso94 – 2017-10-11T01:18:56.687

MATL, 41 bytes

:Q1y"XHyw)Zp?5MQ}1MtYf1)/H(8MyfHq=*+9M]]&

Output is 1-based. The program times out for the last test case in the online interpreter.

Try it online!

Explanation

The program applies the procedure as described in the challenge. To do so, it makes unusually heavy use of MATL's manual and automatic clipboards.

The smallest divisor is obtained as the first entry in the prime factor decomposition.

The "divide" update is done by overwriting the corresponding entry of array A. The "add" update is done by element-wise adding to A an array that contains zeros except at the desired position.

:Q        % Implicitly input n. Push array [2 3 ... n+1]. This is the initial array A. 
          % It contains all required positions. Some values will be overwritten
1         % Push 1. This is the initial value for p
y         % Duplicate from below
"         % For each loop. This executes the following n times.
          %   STACK (contents whosn bottom to top): A, p
  XH      %   Copy p into clipboard H
  y       %   Duplicate from below. STACK: A, p, A
  w       %   Swap. STACK: A, A, p
  )       %   Reference indexing. STACK: A, A[p]
  Zp      %   Isprime. STACK: A, false/true
  ?       %   If true (that is, if A[p] is prime)
    5M    %     Push p from automatic clipboard. STACK: A, p
    Q     %     Add 1. STACK: A, p+1
  }       %   Else (that is, if A[p] is not prime)
    1M    %     Push A[p] from automatic clipboard. STACK: A, A[p]
    t     %     Duplicate. STACK: A, A[p], A[p]
    Yf    %     Prime factors, with repetitions. STACK: A, A[p], prime factors of A[p]
    1)    %     Get first element, d. STACK: A, A[p], d
    /     %     Divide. STACK: A, A[p]/d
    H     %     Push p from clipboard H. STACK: A, A[p]/d, p
    (     %     Assignment indexing: write value. STACK: A with A[p] updated
    8M    %     Push d from automatic clipboard.
    y     %     Duplicate from below. STACK: A with A[p] updated, d, A with A[p] updated
    f     %     Find: push indices of nonzero entries.
          %     STACK: A with A[p] updated, d, [1 2 ... n]
    Hq    %     Push p from clipboard H, subtract 1.
          %     STACK: A with A[p] updated, d, [1 2 ... n], p-1
    =     %     Test for equality, element-wise.
          %     STACK: A with A[p] updated, d, [0 ... 0 1 0 ... 0]
    *     %     Multiply, element-wise. STACK: A with A[p] updated, [0 ... 0 d 0 ... 0]
    +     %     Add, element-wise. STACK: A with A[p-1] and A[p] updated
    9M    %     Push p-1 from automatic clipboard.
          %     STACK: A with A[p-1] and A[p] updated, p-1
  ]       %   End if. The stack contains the updated array and index
]         % End for each. Process the next iteration
&         % Specify that the following implicit display function should display only
          % the top of the stack. Implicitly display

Luis Mendo

Posted 2017-10-09T02:28:45.480

Reputation: 87 464

Pyth - 44 bytes

Straightforward procedural implementation.

K}2hhQVQJ@KZIP_J=hZ).?=GhPJ XKZ/JG=tZ XZKG;Z

Test Suite.

Maltysen

Posted 2017-10-09T02:28:45.480

Reputation: 25 023

PARI/GP, 87 bytes

f(n)=A=[2..9^5];p=1;for(i=1,n,q=factor(A[p])[1,1];if(A[p]-q,A[p]/=q;p--;A[p]+=q,p++));p

Pretty self-explanatory (not so golf-ish). If you do not count the f(n)= part, that is 82 bytes. You can also start by n-> (85 bytes).

It is a 1-indexed language.

Edit: The modification illustrate(n,m)=A=[2..m+1];p=1;for(i=1,n,for(j=1,m,printf("%5s",if(j==p,Str(">",A[j],"<"),Str(A[j]," "))));print();q=factor(A[p])[1,1];if(A[p]!=q,A[p]/=q;p--;A[p]+=q,p++)) will print an illustration of the ant's walk (given a wide enough terminal). For example illustrate(150,25) will give the first 150 steps on 25 columns, like this:

  >2<   3    4    5    6    7    8    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2   >3<   4    5    6    7    8    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    3   >4<   5    6    7    8    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2   >5<   2    5    6    7    8    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5   >2<   5    6    7    8    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    2   >5<   6    7    8    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    2    5   >6<   7    8    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    2   >7<   3    7    8    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    2    7   >3<   7    8    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    2    7    3   >7<   8    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    2    7    3    7   >8<   9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    2    7    3   >9<   4    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    2    7   >6<   3    4    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    2   >9<   3    3    4    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5   >5<   3    3    3    4    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5   >3<   3    3    4    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3   >3<   3    4    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3   >3<   4    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    3   >4<   9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3   >5<   2    9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5   >2<   9   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    2   >9<  10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5   >5<   3   10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    5   >3<  10   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    5    3  >10<  11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    5   >5<   5   11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    5    5   >5<  11   12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    5    5    5  >11<  12   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    5    5    5   11  >12<  13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    5    5    5  >13<   6   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    5    5    5   13   >6<  13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    5    5    5  >15<   3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    5    5   >8<   5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    5   >7<   4    5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    5    7   >4<   5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5    5   >9<   2    5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    5   >8<   3    2    5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3   >7<   4    3    2    5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3    7   >4<   3    2    5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3    3   >9<   2    3    2    5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    3   >6<   3    2    3    2    5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5   >5<   3    3    2    3    2    5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5   >3<   3    2    3    2    5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3   >3<   2    3    2    5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3   >2<   3    2    5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2   >3<   2    5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3   >2<   5    3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2   >5<   3   13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    5   >3<  13   14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    5    3  >13<  14   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    5    3   13  >14<  15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    5    3  >15<   7   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    5   >6<   5    7   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2   >7<   3    5    7   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7   >3<   5    7   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7    3   >5<   7   15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7    3    5   >7<  15   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7    3    5    7  >15<  16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7    3    5  >10<   5   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7    3   >7<   5    5   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7    3    7   >5<   5   16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7    3    7    5   >5<  16   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7    3    7    5    5  >16<  17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7    3    7    5   >7<   8   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7    3    7    5    7   >8<  17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7    3    7    5   >9<   4   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7    3    7   >8<   3    4   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7    3   >9<   4    3    4   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2    7   >6<   3    4    3    4   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    2   >9<   3    3    4    3    4   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3   >5<   3    3    3    4    3    4   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5   >3<   3    3    4    3    4   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3   >3<   3    4    3    4   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3   >3<   4    3    4   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    3   >4<   3    4   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3   >5<   2    3    4   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5   >2<   3    4   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2   >3<   4   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    3   >4<  17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2   >5<   2   17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    5   >2<  17   18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    5    2  >17<  18   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    5    2   17  >18<  19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    5    2  >19<   9   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    5    2   19   >9<  19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    5    2  >22<   3   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    5   >4<  11    3   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2   >7<   2   11    3   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7   >2<  11    3   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    2  >11<   3   19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    2   11   >3<  19   20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    2   11    3  >19<  20   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    2   11    3   19  >20<  21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    2   11    3  >21<  10   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    2   11   >6<   7   10   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    2  >13<   3    7   10   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    2   13   >3<   7   10   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    2   13    3   >7<  10   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    2   13    3    7  >10<  21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    2   13    3   >9<   5   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    2   13   >6<   3    5   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    2  >15<   3    3    5   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7   >5<   5    3    3    5   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5   >5<   3    3    5   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5   >3<   3    5   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3   >3<   5   21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    3   >5<  21   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    3    5  >21<  22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    3   >8<   7   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3   >5<   4    7   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    5   >4<   7   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3   >7<   2    7   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7   >2<   7   22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    2   >7<  22   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    2    7  >22<  23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    2   >9<  11   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7   >5<   3   11   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    5   >3<  11   23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    5    3  >11<  23   24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    5    3   11  >23<  24   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    5    3   11   23  >24<  25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    5    3   11  >25<  12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    5    3  >16<   5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    5   >5<   8    5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    5    5   >8<   5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    5   >7<   4    5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    5    7   >4<   5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7    5   >9<   2    5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3    7   >8<   3    2    5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5    3   >9<   4    3    2    5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    5   >6<   3    4    3    2    5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5   >7<   3    3    4    3    2    5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7   >3<   3    4    3    2    5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3   >3<   4    3    2    5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    3   >4<   3    2    5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3   >5<   2    3    2    5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5   >2<   3    2    5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5    2   >3<   2    5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5    2    3   >2<   5   12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5    2    3    2   >5<  12   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5    2    3    2    5  >12<  25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5    2    3    2   >7<   6   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5    2    3    2    7   >6<  25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5    2    3    2   >9<   3   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5    2    3   >5<   3    3   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5    2    3    5   >3<   3   25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5    2    3    5    3   >3<  25   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5    2    3    5    3    3  >25<  26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5    2    3    5    3   >8<   5   26
   2    5    5    5    3    3    2    3    5    3    3    5    2    7    5    7    3    5    2    3    5   >5<   4    5   26

Jeppe Stig Nielsen

Posted 2017-10-09T02:28:45.480

Reputation: 602

Python 3, 158 149 133 bytes

This is a straightforward procedural implementation with one or two quirks to make sure the code works for all test cases. I use [*range(2,n+9)] to ensure that A is large enough (except for n<3, n+9 is more than enough). The else clause divides the old A[p] by d, decrements p, and then adds d to the new A[p], which is definitely bad coding practice. Otherwise, pretty straightforward. Golfing suggestions welcome!

Edit: -9 bytes without sympy thanks to Halvard Hummel. -14 bytes from Felipe Nardi Batista, -6 bytes from some cues from Jonathan Frech's Python 2 answer

p,_,*A=range(int(input())+2)
for _ in A:
 m=A[p];d=min(k for k in range(2,m+1)if m%k<1);p+=1
 if d<m:A[p-1]//=d;p-=2;A[p]+=d
print(p)

Try it online!

Sherlock9

Posted 2017-10-09T02:28:45.480

Reputation: 11 664

145 bytes – Halvard Hummel – 2017-10-09T09:57:22.140

148 bytes by making it a full program – Felipe Nardi Batista – 2017-10-09T10:54:35.687

if d-m:A[p]... and else:p+=1 to save a byte – Felipe Nardi Batista – 2017-10-09T10:55:44.450

143 bytes by removing the else statement – Felipe Nardi Batista – 2017-10-09T11:06:58.170

after removing the else statement, there is no difference in bytes to the function version – Felipe Nardi Batista – 2017-10-09T11:10:16.200

139 bytes by using unpacking in the creation of p and A – Felipe Nardi Batista – 2017-10-09T11:12:10.433

Python 2, 142 127 bytes

Saved fifteen bytes thanks to Sherlock9.

T=range(2,input()+2);p=0
for _ in T:
 m=T[p];d=min(k for k in range(2,m+1)if m%k<1);p+=1
 if d<m:T[p-1]/=d;p-=2;T[p]+=d
print p

Try it online!

Jonathan Frech

Posted 2017-10-09T02:28:45.480

Reputation: 6 681

127 bytes if you don't use P(n) – Sherlock9 – 2017-10-09T06:30:27.767

126 bytes – Felipe Nardi Batista – 2017-10-09T11:41:44.777

@FelipeNardiBatista Unfortunately, your suggestion doesn't seem to work for test cases n<=4 – Sherlock9 – 2017-10-09T13:56:33.363

Mathematica, 118 103 bytes

(s=Range[2,5^6];t=1;Do[If[PrimeQ@s[[t]],t++,s[[t]]/=(k=#2&@@ Divisors@s[[t]]);s[[t-1]]+=k;t--],#];t-1)&

Try it online!

Martin Ender saved 15 bytes

J42161217

Posted 2017-10-09T02:28:45.480

Reputation: 15 931

You'd got a stray space in front of Divisors, you can use infix notation for Do, and you can just return t instead of t-1 (1-based result). – Martin Ender – 2017-10-09T16:16:19.253

PHP, 102+1 bytes

for($a=range(2,$argn);$argn--;$d<$a[+$p]?$a[$p--]/=$d+!$a[$p]+=$d:$p++)for($d=1;$a[+$p]%++$d;);echo$p;

Run as pipe with -R or try it online.

Empty output for input 0; insert + after echo for a literal 0

or use this 1-indexed version (103+1 bytes):

for($a=range($p=1,$argn);$argn--;$d<$a[$p]?$a[$p--]/=$d+!$a[$p]+=$d:$p++)for($d=1;$a[$p]%++$d;);echo$p;

Titus

Posted 2017-10-09T02:28:45.480

Reputation: 13 814

C (gcc), 152 148 bytes

Minified

int f(int n){int*A=malloc(++n*4),p=0,i,q;for(i=0;i<n;i++)A[i]=i+2;for(i=1;i<n;i++){for(q=2;A[p]%q;q++);if(A[p++]>q){A[--p]/=q;A[--p]+=q;}}return p;}

Formated with some comments

int f(int n) {
  int *A = malloc(++n * 4), p = 0, i, q;
  // Initialize array A
  for (i = 0; i < n; i++)
    A[i] = i + 2;
  // Do n step (remember n was incremented)
  for (i = 1; i < n; i++) {
    // Find smallest divisor
    for (q = 2; A[p] % q; q++)
      ;
    if (A[p++] > q) {
      A[--p] /= q;
      A[--p] += q;
    }
  }
  return p;
}

Main function for testing

#include <stdlib.h>
#include <stdio.h>
int main(int argc, char **argv) {
  if (argc != 2)
    return 2;
  int n = atoi(argv[1]);
  int p = f(n);
  printf("%d => %d\n", n, p);
  return 0;
}

For showing each step

Declare display() inside f()

int f(int n) {
  int *A = malloc(++n * 4), p = 0, i, q;
  void display(void) {
    for (int i=0; i < p; i++) {
      printf(" %d", A[i]);
    }
    printf(" \033[1;31m%d\033[m", A[p]);
    if (p+1 < n)
      printf(" %d", A[p+1]);
    printf("\n");
  }
  ...

Call display()
```
  A[i] = i + 2;
display();
```
Call display()
```
  }
  display();
}
```

user285259

Posted 2017-10-09T02:28:45.480

Reputation: 201

You can shave off some bytes by declaring A as an array and initializing your loop controls prior to the loops where possible, right?

– Reinstate Monica – 2019-04-25T15:04:05.667

R, 123 bytes

A straightforward implementation. It is provided as a function, which takes the number of moves as input and returns the position p.

It loops over the sequence and moves the pointer forth and back according to the rules. The output is 0-based.

A note: in order to find the smallest prime factor of a number x, it computes the modulus of x relative to all integers from 0 to x. It then extracts the numbers with modulus equal to 0, which are always [0,1,...,x]. If the third such number is not x, then it is the smallest prime factor of x.

p=function(l){w=0:l;v=w+1;j=1;for(i in w){y=v[j];x=w[!y%%w][3]
if(x%in%c(NA,y))j=j+1
else{v[j]=y/x;j=j-1;v[j]=v[j]+x}}
j-2}

Try it online!

NofP

Posted 2017-10-09T02:28:45.480

Reputation: 754

Clojure, 185 bytes

#(loop[[n p][(vec(range 2 1e3))0]i %](if(= i 0)p(recur(if-let[q(first(for[i(range 2(n p)):when(=(mod(n p)i)0)]i))][(assoc n p(/(n p)q)(dec p)(+(n(dec p))q))(dec p)][n(inc p)])(dec i))))

Ouch, editing a "state" is not ideal in Clojure. You'll need to increase the exponent for larger inputs.

NikoNyrh

Posted 2017-10-09T02:28:45.480

Reputation: 2 361

Why did you use pattern matching in the loop? You should be able to lose a few bytes without that. – clismique – 2017-10-12T07:21:12.417

Also, you might be able to change the first thing to a some statement. – clismique – 2017-10-12T07:35:03.437

Without pattern matching I had to repeat recur twice, one for each if-let branch. Also (dec i) would be duplicated. some needs a predicate, I could use + as we are dealing with numbers but this is one character longer than first. CMIIW – NikoNyrh – 2017-10-12T07:59:37.973

Java 8, 138 135 bytes

n->{int a[]=new int[++n],s=0,p=0,j=0;for(;j<n;a[j++]=j+1);for(;++s<n;p++)for(j=1;++j<a[p];)if(a[p]%j<1){a[p--]/=j;a[p--]+=j;}return p;}

Explanation:

Try it here.

n->{                     // Method with integer as both parameter and return-type
  int a[]=new int[++n],  //  Integer-array with a length of `n+1`
      s=0,               //  Steps-counter (starting at 0)
      p=0,               //  Current position (starting at 0)
      j=0;               //  Index integer (starting at 0)
  for(;j<n;              //  Loop (1) from 0 to the input (inclusive due to `++n` above)
    a[j++]=j+1           //   And fill the array with 2 through `n+2`
  );                     //  End of loop (1)
  for(;++s<n;            //  Loop (2) `n` amount of steps:
      p++)               //    And after every iteration: increase position `p` by 1
    for(j=1;             //   Reset `j` to 1
        ++j<a[p];)       //   Inner loop (3) from 2 to `a[p]` (the current item)
      if(a[p]%j<1){      //    If the current item is divisible by `j`:
        a[p--]/=j;       //     Divide the current item by `j`
        a[p--]+=j;}      //     And increase the previous item by `j`
                         //     And set position `p` two steps back (with both `p--`)
                         //   End of inner loop (3) (implicit / single-line body)
                         //  End of loop (2) (implicit / single-line body)
  return p;              //  Return the resulting position `p`
}                        // End of method

Kevin Cruijssen

Posted 2017-10-09T02:28:45.480

Reputation: 67 575

Clojure, 198 193 191 bytes

This needs to be severely golfed...

#(loop[i(vec(range 2(+ % 9)))c 0 p 0](if(= % c)p(let[d(dec p)u(i p)f(some(fn[n](if(=(mod u n)0)n))(range 2(inc u)))e(= u f)](recur(if e i(assoc i d(+(i d)f)p(/ u f)))(inc c)(if e(inc p)d)))))

Golf 1: Saved 5 bytes by changing (first(filter ...)) to (some ...)

Golf 2: Saved 2 bytes by changing (zero? ...) to (= ... 0)

Usage:

(#(...) 10000) => 512

Ungolfed code:

(defn prime-ant [n]
  (loop [counter 0
         pos 0
         items (vec (range 2 (+ n 9)))]
    (if (= n counter) pos
      (let [cur-item (nth items pos)
            prime-factor
            (some #(if (zero? (mod cur-item %)) %)
              (range 2 (inc cur-item)))
            equals? (= cur-item prime-factor)]
        (recur
          (inc counter)
          (if equals? (inc pos) (dec pos))
          (if equals? items
            (assoc items
              (dec pos) (+ (items (dec pos)) prime-factor)
              pos (/ cur-item prime-factor))))))))

clismique

Posted 2017-10-09T02:28:45.480

Reputation: 6 600

The prime ant

Answers

Alice, 45 bytes

Octave, 109 103 101 94 bytes

MATLAB, 130 123 118 117 bytes

Python 2, 120 bytes

JavaScript (ES6), 91 bytes

Demo

Haskell, 108 106 94 bytes

TI-BASIC, 108 103 102 98 bytes

MATL, 41 bytes

Explanation

Pyth - 44 bytes

PARI/GP, 87 bytes

Python 3, 158 149 133 bytes

Python 2, 142 127 bytes

Mathematica, 118 103 bytes

PHP, 102+1 bytes

C (gcc), 152 148 bytes

Minified

Formated with some comments

Main function for testing

For showing each step

R, 123 bytes

Clojure, 185 bytes

Java 8, 138 135 bytes

Clojure, 198 193 191 bytes

Usage:

Ungolfed code: