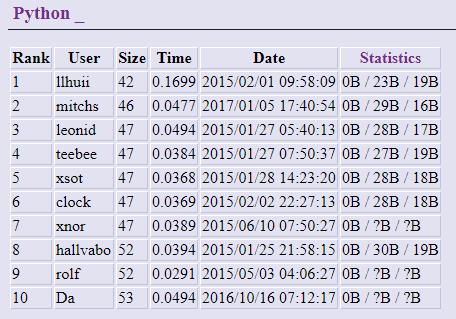
Getting 39 bytes
This is an explanation of how I got a 39-byte solution, which Dennis and JonathanFrech found separately as well. Or, rather, it explains how one could arrive at the answer in hindsight, in a way that's much nicer than my actual path to it, which was full of muddy reasoning and dead ends.
n=0
exec"print n;n=n+2^-(n+2^n)%3;"*400
Writing this a bit less golfed and with more parens, this looks like:
n=0
for _ in range(400):
print n
n=(n+2)^(-((n+2)^n))%3
Bit parities
We start with an idea from my 47-byte solution to output all numbers of the form n=2*k+b where k counts up 0,1,...,399 and b is a parity bit that makes the overall number of 1's even.
Let's write par(x) for the bit parity of x, that is the xor (^) all of bits in x. This is 0 if there's an even number of 1-bits (number is evil), and 1 if there's an odd number of 1-bits. For n=2*k+b, we have par(n) = par(k)^b, so to achieve evil par(n)==0 we need b=par(k), i.e. the last bit of n to be the bit parity of the preceding bits.
My first efforts at golfing were on expressing the par(k), at first directly with bin(k).count('1')%2, and then with bit manipulation.
Parity updates
Still, there didn't seem to be a short expression. Instead, it helped to realize that there's more info to work with. Rather than just computing the bit parity of the current number,
k ----> par(k)
we can update the bit parity as we increment k to k+1.
k ----> par(k)
|
v
k+1 ----> par(k+1)
That is, since we're counting up k=0,1,2,..., we merely need to maintain the current bit parity rather than calculating it from scratch each time. The bit parity update par(k+1)^par(k) is the parity of the number of bits flipped in going from k to k+1, that is par((k+1)^k).
par(k+1) ^ par(k) = par((k+1)^k)
par(k+1) = par(k) ^ par((k+1)^k)
Form of (k+1)^k
Now we need to compute par((k+1)^k). It might seem like we've gotten nowhere because computing bit parity is exactly the problem we're trying to solve. But, numbers expressed as (k+1)^k have the form 1,3,7,15,.., that is one below a power of 2, a fact often used in bit hacks. Let's see why that is.
When we increment k, the effect of the binary carries is to invert the last 0 and all 1's to its right, creating a new leading 0 if there were none. For example, take k=43=0b101011
**
101011 (43)
+ 1
------
= 101100 (44)
101011 (43)
^101100 (44)
------
= 000111 (77)
The columns causing a carry are marked with *. These have a 1 change to a 0 and pass on a carry bit of 1, which keeps propagating left until it hits a 0 in k, which changes to 1. Any bits further to the left are unaffected. So, when k^(k+1) checks which bit positions change k to k+1, it finds the positions of the rightmost 0 and the 1's to its right. That is, the changed bits form a suffix, so result is 0's followed by one or more 1's. Without the leading zeroes, there are binary numbers 1, 11, 111, 1111, ... that are one below a power of 2.
Computing par((k+1)^k)
Now that we understand that (k+1)^k is limited to 1,3,7,15,..., let's find a way to compute the bit parity of such numbers. Here, a useful fact is that 1,2,4,8,16,... alternate modulo 3 between 1 and 2, since 2==-1 mod 3 . So, taking 1,3,7,15,31,63... modulo 3 gives 1,0,1,0,1,0..., which are exactly their bit parities. Perfect!
So, we can do the update par(k+1) = par(k) ^ par((k+1)^k) as
par(k+1) = par(k) ^ ((k+1)^k)%3
Using b as the variable we're storing the parity in, this looks like
b^=((k+1)^k)%3
Writing the code
Putting this together in code, we start k and the parity bit b both at 0, then repeatedly print n=2*k+b and update b=b^((k+1)^k)%3 and k=k+1.
46 bytes
k=b=0
exec"print 2*k+b;b^=(k+1^k)%3;k+=1;"*400
Try it online!
We removed parens around k+1 in ((k+1)^k)%3 because Python precedence does the addition first anyway, weird as it looks.
Code improvements
We can do better though by working directly with a single variable n=2*k+b and performing the updates directly on it. Doing k+=1 corresponds to n+=2. And, updating b^=(k+1^k)%3 corresponds to n^=(k+1^k)%3. Here, k=n/2 before updating n.
44 bytes
n=0
exec"print n;n^=(n/2+1^n/2)%3;n+=2;"*400
Try it online!
We can shorten n/2+1^n/2 (remember this is (n/2+1)^n/2) by rewriting
n/2+1 ^ n/2
(n+2)/2 ^ n/2
(n+2 ^ n)/2
Since /2 removes the last bit, it doesn't matter if we do it before or after xor-ing. So, we have n^=(n+2^n)/2%3. We can save another byte by noting that modulo 3, /2 is equivalent to *2 is equivalent to -, noting that n+2^n is even so the division is actual halving without flooring. This gives n^=-(n+2^n)%3
41 bytes
n=0
exec"print n;n^=-(n+2^n)%3;n+=2;"*400
Try it online!
Finally, we can combine the operations n^=c;n+=2 into n=(n+2)^c, where c is a bit. This works because ^c acts only on the last bit and +2 doesn't care about the last bit, so the operations commute. Again, precedence lets us omit parens and write n=n+2^c.
39 bytes
n=0
exec"print n;n=n+2^-(n+2^n)%3;"*400
Try it online!
2
It may also be worthy to note that this sequences is "Indices of zeros in the Thue-Morse sequence A010060." (source: oeis)
– Conor O'Brien – 2017-09-29T01:38:22.857