95
27
As of 13/03/2018 16:45 UTC, the winner is answer #345, by Scrooble. This means the contest is officially over, but feel free to continue posting answers, just so long as they follow the rules.
As well, just a quick shout out to the top three answerers in terms of numbers of answers:
1. NieDzejkob - 41 answers
2. KSmarts - 30 answers
3. Hyper Neutrino - 26 answers
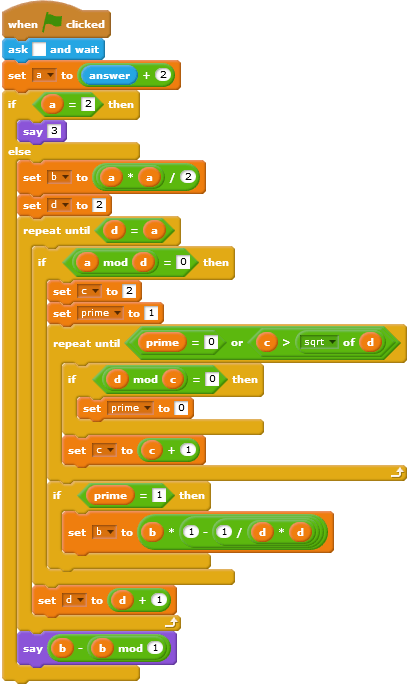
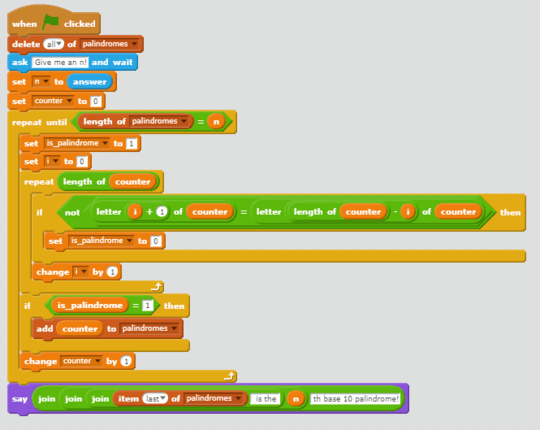
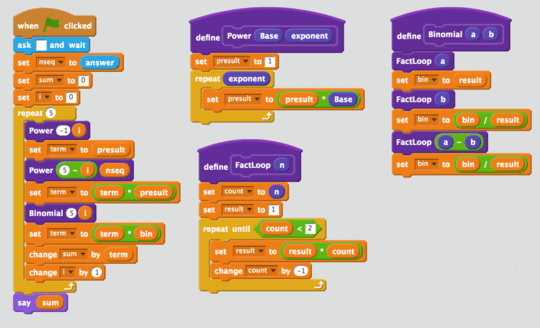
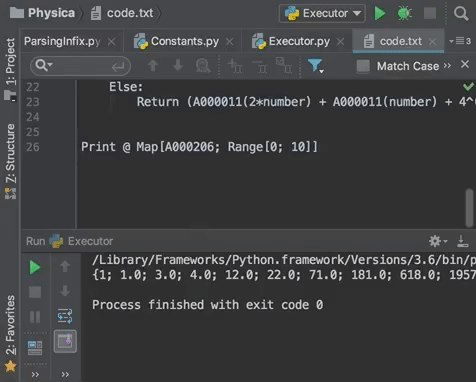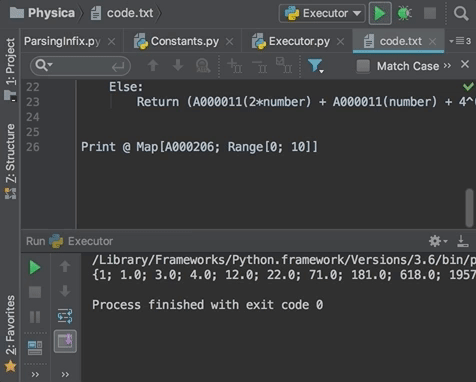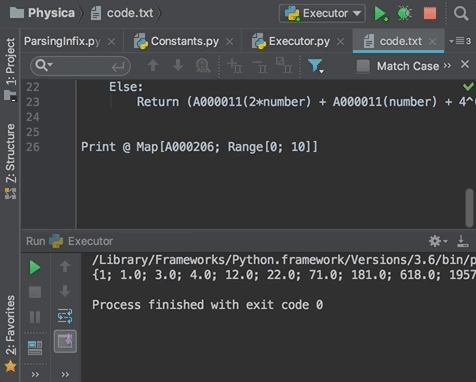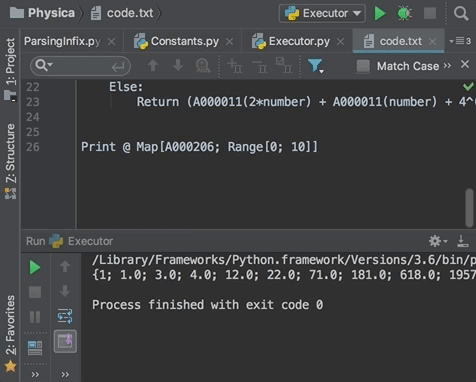
This is an answer chaining question that uses sequences from OEIS, and the length of the previous submission.
This answer chaining question will work in the following way:
- I will post the first answer. All other solutions must stem from that.
- The next user (let's call them userA) will find the OEIS sequence in which its index number (see below) is the same as the length of my code.
- Using the sequence, they must then code, in an unused language, a program that takes an integer as input, n, and outputs the nth number in that sequence.
- Next, they post their solution after mine, and a new user (userB) must repeat the same thing.
The nth term of a sequence is the term n times after the first, working with the first value being the first value given on its OEIS page. In this question, we will use 0-indexing for these sequences. For example, with A000242 and n = 3, the correct result would be 25.
However!
This is not a code-golf, so shortest code doesn't matter. But the length of your code does still have an impact. To prevent the duplication of sequences, your bytecount must be unique. This means that no other program submitted here can be the same length in bytes as yours.
If there isn't a sequence for then length of the last post, then the sequence for your post is the lowest unused sequence. This means that the sequences used also have to be unique, and that the sequence cannot be the same as your bytecount.
After an answer has been posted and no new answers have been posted for more than a week, the answer before the last posted (the one who didn't break the chain) will win.
Input and Output
Generic input and output rules apply. Input must be an integer or a string representation of an integer and output must be the correct value in the sequence.
Formatting
As with most answer-chaining questions, please format your answer like this
# N. language, length, [sequence](link)
`code`
[next sequence](link)
*anything else*
Rules
- You must wait for at least 1 hour before posting an answer, after having posted.
- You may not post twice (or more) in a row.
- The index number of a sequence is the number after the
Apart, and with leading zeros removed (e.g. forA000040the index number is 40) - You can assume that neither the input nor the required output will be outside your languages numerical range, but please don't abuse this by choosing a language that can only use the number 1, for example.
- If the length of your submission is greater than 65536 characters long, please provide a link to a way to access the code (pastebin for example).
nwill never be larger than 1000, or be out of bounds for the sequence, simply to prevent accuracy discrepancies from stopping a language from competing.- Every 150 (valid) answers, the number of times a language may be used increases. So after 150 solutions have been posted, every language may be used twice (with all previous answers counting towards this). For instance, when 150 answers have been posted, Python 3 may be used twice, but due to the fact that it has already been used once, this means it can only be used once more until 300 answers have been posted.
- Please be helpful and post a link to the next sequence to be used. This isn't required, but is a recommendation.
- Different versions of languages, e.g. Python 2 and Python 3 are different languages. As a general rule, if the different versions are both available on Try It Online, they are different languages, but keep in mind that this is a general rule and not a rigid answer.
- It is not banned, but please try not to copy the code from the OEIS page, and actually try to solve it.
- Hardcoding is only allowed if the sequence is finite. Please note that the answer that prompted this (#40) is the exception to the rule. A few answers early in the chain hardcode, but these can be ignored, as there is no good in deleting the chain up to, say, #100.
Answer chain snippet
var QUESTION_ID=133754,OVERRIDE_USER=66833;function shareUrl(i){return"https://codegolf.stackexchange.com/a/"+i}function answersUrl(e){return"https://api.stackexchange.com/2.2/questions/"+QUESTION_ID+"/answers?page="+e+"&pagesize=100&order=desc&sort=creation&site=codegolf&filter="+ANSWER_FILTER}function commentUrl(e,s){return"https://api.stackexchange.com/2.2/answers/"+s.join(";")+"/comments?page="+e+"&pagesize=100&order=desc&sort=creation&site=codegolf&filter="+COMMENT_FILTER}function getTemplate(s){return jQuery(jQuery("#answer-template").html().replace("{{PLACE}}",s.index+".").replace("{{NAME}}",s.user).replace("{{LANGUAGE}}",s.language).replace("{{SEQUENCE}}",s.sequence).replace("{{SIZE}}",s.size).replace("{{LINK}}",s.link))}function search(l,q){m=jQuery("<tbody id='answers'></tbody>");e.forEach(function(s){if(!q||(l==0&&RegExp('^'+q,'i').exec(s.lang_name))||(l==1&&q===''+s.size)){m.append(jQuery(getTemplate(s)))}});jQuery("#answers").remove();jQuery(".answer-list").append(m)}function sortby(ix){t=document.querySelector('#answers');_els=t.querySelectorAll('tr');els=[];for(var i=0;i<_els.length;i++){els.push(_els[i]);}els.sortBy(function(a){a=a.cells[ix].innerText;return ix==0||ix==4?Number(a):a.toLowerCase()});for(var i=0;i<els.length;i++)t.appendChild(els[i]);}function checkSize(x){if(!x)return jQuery("#size-used").text("");var i=b.indexOf(+x);if(i<0)return jQuery("#size-used").text("Available!");var low=+x,high=+x;while(~b.indexOf(low))low--;while(~b.indexOf(high))high++;jQuery("#size-used").text(("Not available. The nearest are "+low+" and "+high).replace("are 0 and","is"))}function checkLang(x){}function getAnswers(){jQuery.ajax({url:answersUrl(answer_page++),method:"get",dataType:"jsonp",crossDomain:!0,success:function(e){answers.push.apply(answers,e.items),answers_hash=[],answer_ids=[],e.items.forEach(function(e){e.comments=[];var s=+e.answer_id;answer_ids.push(s),answers_hash[s]=e}),e.has_more||(more_answers=!1),comment_page=1,getComments()}})}function getComments(){jQuery.ajax({url:commentUrl(comment_page++,answer_ids),method:"get",dataType:"jsonp",crossDomain:!0,success:function(e){e.items.forEach(function(e){e.owner.user_id===OVERRIDE_USER&&answers_hash[e.post_id].comments.push(e)}),e.has_more?getComments():more_answers?getAnswers():process()}})}function getAuthorName(e){return (e.owner.user_id==OVERRIDE_USER?"<span id='question-author'>"+e.owner.display_name+"</span>":e.owner.display_name)}function process(){b=[];c=[];answers.forEach(function(s){var r=s.body;s.comments.forEach(function(e){OVERRIDE_REG.test(e.body)&&(r="<h1>"+e.body.replace(OVERRIDE_REG,"")+"</h1>")});var a=r.match(SCORE_REG);if(a){e.push({user:getAuthorName(s),size:+a[4],language:a[2],lang_name:a[3],index:+a[1],sequence:a[5],link:shareUrl(s.answer_id)});if(b.indexOf(+a[4])>=0&&c.indexOf(+a[4])<0){c.push(+a[4])};b.push(+a[4])}else{jQuery('#weird-answers').append('<a href="'+shareUrl(s.answer_id)+'">This answer</a> is not formatted correctly. <b>Do not trust the information provided by this snippet until this message disappears.</b><br />')}}),e.sortBy(function(e){return e.index});e.forEach(function(e){jQuery("#answers").append(getTemplate(e))});var q="A"+("000000"+e.slice(-1)[0].size).slice(-6);jQuery("#next").html("<a href='http://oeis.org/"+q+"'>"+q+"</a>");c.forEach(function(n){jQuery('#weird-answers').append('The bytecount '+n+' was used more than once!<br />')})}Array.prototype.sortBy=function(f){return this.sort(function(a,b){if(f)a=f(a),b=f(b);return(a>b)-(a<b)})};var ANSWER_FILTER="!*RB.h_b*K(IAWbmRBLe",COMMENT_FILTER="!owfmI7e3fd9oB",answers=[],answers_hash,answer_ids,answer_page=1,more_answers=!0,comment_page,e=[];getAnswers();var SCORE_REG=/<h\d>\s*(\d+)\.\s*((?:<a [^>]+>\s*)?((?:[^\n,](?!<\/a>))*[^\s,])(?:<\/a>)?),.*?(\d+)(?=[^\n\d<>]*(?:<(?:s>[^\n<>]*<\/s>|[^\n<>]+>)[^\n\d<>]*)*, ((?:<a[^>]+>\s*)?A\d+(?:\s*<\/a>)?)\s*<\/h\d>)/,OVERRIDE_REG=/^Override\s*header:\s*/i;body{text-align:left!important;font-family:Roboto,sans-serif}#answer-list,#language-list{padding:10px;/*width:290px*/;float:left;display:flex;flex-wrap:wrap;list-style:none;}table thead{font-weight:700}table td{padding:5px}ul{margin:0px}#board{display:flex;flex-direction:column;}#language-list li{padding:2px 5px;}#langs-tit{margin-bottom:5px}#byte-counts{display:block;margin-left:15px;}#question-author{color:purple;text-shadow: 0 0 15px rgba(128,0,128,0.1);}#label-info{font-weight: normal;font-size: 14px;font-style: italic;color: dimgray;padding-left: 10px;vertical-align: middle; }<script src="https://ajax.googleapis.com/ajax/libs/jquery/2.1.1/jquery.min.js"></script><link rel="stylesheet" type="text/css" href="//cdn.sstatic.net/codegolf/all.css?v=83c949450c8b"><p id="weird-answers"></p><p>Currently waiting on <span id="next"></span></p><span>Search by Byte Count: <input id="search" type="number" min=1 oninput="checkSize(this.value);search(1,this.value)" onclick="document.getElementById('search2').value='';!this.value&&search(0,'')"/> <span id="size-used"></span></span><br><span>Search by Language: <input id="search2" oninput="checkLang(this.value);search(0,this.value)" onclick="document.getElementById('search').value='';!this.value&&search(0,'')"/> <span id="language-used"></span></span><h2>Answer chain <span id="label-info">click a label to sort by column</span></h2><table class="answer-list"><thead><tr><td onclick="sortby(0)">#</td><td onclick="sortby(1)">Author</td><td onclick="sortby(2)">Language</td><td onclick="sortby(3)">Sequence</td><td onclick="sortby(4)">Size</td></tr></thead><tbody id="answers"></tbody></table><table style="display: none"><tbody id="answer-template"><tr><td>{{PLACE}}</td><td>{{NAME}}</td><td>{{LANGUAGE}}</td><td>{{SEQUENCE}}</td><td>{{SIZE}}</td><td><a href="{{LINK}}">Link</a></td></tr></tbody></table><table style="display: none"><tbody id="language-template"><tr><td>{{LANGUAGE}}</td><td>{{NAME}}</td><td>{{SEQUENCE}}</td><td>{{SIZE}}</td><td><a href="{{LINK}}">Link</a></td></tr></tbody></table>






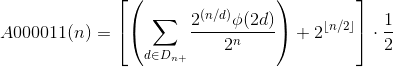
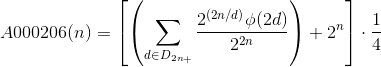
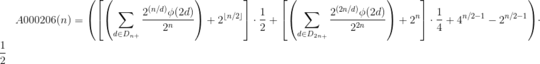
Comments are not for extended discussion; this conversation has been moved to chat.
– Dennis – 2017-10-31T02:49:10.023Is it OK if a program would need a better floating-point accuracy for the builtin
float/doubletype in order to produce values for largern? – NieDzejkob – 2017-11-21T15:15:01.370@NieDzejkob Assuming that it was only limited by memory and/or time, and would theoretically work if given infinite time and memory, then yes. – caird coinheringaahing – 2017-11-21T15:42:31.600
@cairdcoinheringaahing that's not what I'm talking about, check the most recent (swift) answer. – NieDzejkob – 2017-11-21T15:55:18.197
@NieDzejkob In that case, yes it's acceptable, as the problem isn't with the program. – caird coinheringaahing – 2017-11-21T15:56:57.570
The problem is with the program, though. It's failing to accurately calculate intermediate values which are within the bounds of its types. – Peter Taylor – 2017-11-21T16:27:35.013
@PeterTaylor Sorry, I'm unfamiliar with Swift. If the problem truly is with the answer, and can be corrected, then the answer is invalid. – caird coinheringaahing – 2017-11-21T16:31:23.400
with regards to the hardcoding, I commented here with a rational approximation for gamma that's precise enough to get the first 1001 terms of the continued fraction representation, because it's the rational number represented by the first 1001 terms. Would that count as "hardcoding the sequence"?
– Giuseppe – 2017-12-15T22:12:21.6031@Giuseppe No, as you're generating the numbers by doing the maths, rather than just placing them into an array/string – caird coinheringaahing – 2017-12-15T22:14:18.347
2@cairdcoinheringaahing In my opinion that's hardcoding the gamma constant. It doesn't work "in theory" for larger numbers. – user202729 – 2017-12-22T12:44:09.580
6Chat room – user202729 – 2017-12-22T12:45:17.147
Should
... there is no good in deleted the chain up to ...not rather read... there is no good in deleting the chain up to ...or something similar? – Jonathan Frech – 2018-01-28T17:08:33.417@JonathanFrech Yes it should, corrected. – caird coinheringaahing – 2018-01-28T17:09:40.850