Extreme Fibonacci

Question

There have been a billion iterations of Fibonacci challenges on this website, so lets spice things up with a Fibonacci challenge of a billion iterations!

Your challenge is to output the first 1000 decimal digits of the 1,000,000,000th Fibonacci number with as short a program as possible. This may then optionally be followed by any additional output of your choosing, including but not limited to the rest of the digits.

I am using the convention that fib 0 = 0, fib 1 = 1.

Your program must be fast enough for you to run it and verify its correctness. For this purpose, here are the first 1000 digits:

7952317874554683467829385196197148189255542185234398913453039937343246686182519370050999626136556779332482035723222451226291714456275648259499530612111301255499879639516053459789018700567439946844843034599802419924043753401950114830107234265037841426980398387360784284231996457340782784200767760907777703183185744656536253511502851715963351023990699232595471322670365506482435966586886048627159716916351448788527427435508113909167963907380398242848033980110276370544264285032744364781198451825462130529529633339813483105771370128111851128247136311414208318983802526907917787094802217750859685116363883374847428036737147882079956688807509158372249451437519320162582002000530798309887261257028201907509370554232931107084976854715833585623910450679449120011564762925649144509531904684984417002512086504020779012501356177874199605085558317190905395134468919443313026824813363234190494375599262553025466528838122639433600483849535070647711986769279568548796855207684897741771784375859496425384355879105799

Answer 1

Python 2 + sympy, 72 bytes

from sympy import*
n=sqrt(5)
print'7'+`((.5+n/2)**1e9/n).evalf(1e3)`[2:]

Try it online!

-10 bytes by removing the practically-0 term thanks to Jeff Dege
-1 byte (1000 -> 1e3 thanks to Zacharý)
-2 bytes by removing the unnecessary variable thanks to Erik the Outgolfer
-2 bytes by moving to Python 2 thanks to Zacharý
-3 bytes by 11'ing the -11 thanks to ThePirateBay -3 bytes by swapping str for backticks thanks to notjagan

now beats OP's unposted haskell solution!

Answer 2

Python 2, 106 bytes

a,b=0,1
for c in bin(10**9):
 a,b=2*a*b-a*a,a*a+b*b
 if'1'==c:a,b=b,a+b
 while a>>3340:a/=10;b/=10
print a

Try it online!

No libraries, just integer arithmetic. Runs almost instantly.

The core is the divide-and-conquer identity:

f(2*n)   = 2*f(n)*f(n+1) - f(n)^2
f(2*n+1) = f(n)^2 + f(n+1)^2

This lets us update (a,b) = (f(n),f(n+1)) to double n -> 2*n. Since we want to get n=10**9, this takes only log_2(10**9)=30 iterations. We build n up to 10**9 by repeatedly doing n->2*n+c for each digit c of its binary expansion. When c==1, the doubled value is shifted up 2*n -> 2*n+1 with a one-step Fibonacci shift (a,b)=(b+a,b)

To keep the values a,b manageable, we store only their first 1006 digits by floor-dividing by 10 until they are under 2**3340 ~ 1e1006.

Answer 3

x86 32-bit machine code (with Linux system calls): 106 105 bytes

changelog: saved a byte in the fast version because an off-by-one constant doesn't change the result for Fib(1G).

Or 102 bytes for an 18% slower (on Skylake) version (using mov/sub/cmc instead of lea/cmp in the inner loop, to generate carry-out and wrapping at 10**9 instead of 2**32). Or 101 bytes for a ~5.3x slower version with a branch in the carry-handling in the inner-most loop. (I measured a 25.4% branch-mispredict rate!)

Or 104/101 bytes if a leading zero is allowed. (It takes 1 extra byte to hard-code skipping 1 digit of the output, which is what happens to be needed for Fib(10**9)).

Unfortunately, TIO's NASM mode seems to ignore -felf32 in the compiler flags. Here's a link anyway with my full source code, with all the mess of experimental ideas in comments.

This is a complete program. It prints the first 1000 digits of Fib(10**9) followed by some extra digits (the last few of which are wrong) followed by some garbage bytes (not including a newline). Most of the garbage is non-ASCII, so you may want to pipe through cat -v. It doesn't break my terminal emulator (KDE konsole), though. The "garbage bytes" are storing Fib(999999999). I already had -1024 in a register, so it was cheaper to print 1024 bytes than the proper size.

I'm counting just the machine-code (size of the text segment of my static executable), not the fluff that makes it an ELF executable. (Very tiny ELF executables are possible, but I didn't want to bother with that). It turned out to be shorter to use stack memory instead of BSS, so I can kind of justify not counting anything else in the binary since I don't depend on any metadata. (Producing a stripped static binary the normal way makes a 340 byte ELF executable.)

You could make a function out of this code that you could call from C. It would cost a few bytes to save/restore the stack pointer (maybe in an MMX register) and some other overhead, but also save bytes by returning with the string in memory, instead of making a write(1,buf,len) system call. I think golfing in machine code should earn me some slack here, since nobody else has even posted an answer in any language without native extended-precision, but I think a function version of this should still be under 120 bytes without re-golfing the whole thing.

---

Algorithm:

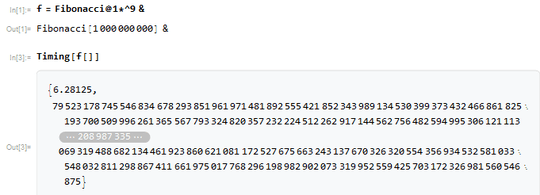
brute force a+=b; swap(a,b), truncating as needed to keep only the leading >= 1017 decimal digits. It runs in 1min13s on my computer (or 322.47 billion clock cycles +- 0.05%) (and could be a few % faster with a few extra bytes of code-size, or down to 62s with much larger code size from loop unrolling. No clever math, just doing the same work with less overhead). It's based on @AndersKaseorg's Python implementation, which runs in 12min35s on my computer (4.4GHz Skylake i7-6700k). Neither version has any L1D cache misses, so my DDR4-2666 doesn't matter.

Unlike Python, I store the extended-precision numbers in a format that makes truncating decimal digits free. I store groups of 9 decimal digits per 32-bit integer, so a pointer offset discards the low 9 digits. This is effectively base 1-billion, which is a power of 10. (It's pure coincidence that this challenge needs the 1-billionth Fibonacci number, but it does save me a couple bytes vs. two separate constants.)

Following GMP terminology, each 32-bit chunk of an extended-precision number is called a "limb". Carry-out while adding has to be generated manually with a compare against 1e9, but is then used normally as an input to the usual ADC instruction for the next limb. (I also have to manually wrap to the [0..999999999] range, rather than at 2^32 ~= 4.295e9. I do this branchlessly with lea + cmov, using the carry-out result from the compare.)

When the last limb produces non-zero carry-out, the next two iterations of the outer loop read from 1 limb higher than normal, but still write to the same place. This is like doing a memcpy(a, a+4, 114*4) to right-shift by 1 limb, but done as part of the next two addition loops. This happens every ~18 iterations.

---

Hacks for size-saving and performance:

• The usual stuff like lea ebx, [eax-4 + 1] instead of mov ebx, 1, when I know that eax=4. And using loop in places where LOOP's slowness only has a tiny impact.

• Truncate by 1 limb for free by offsetting the pointers that we read from, while still writing to the start of the buffer in the adc inner loop. We read from [edi+edx], and write to [edi]. So we can get edx=0 or 4 to get a read-write offset for the destination. We need to do this for 2 successive iterations, first offsetting both, then only offsetting the dst. We detect the 2nd case by looking at esp&4 before resetting the pointers to the front of the buffers (using &= -1024, because the buffers are aligned). See comments in the code.

• The Linux process-startup environment (for a static executable) zeros most registers, and stack-memory below esp/rsp is zeroed. My program takes advantage of this. In a callable-function version of this (where unallocated stack could be dirty), I could use BSS for zeroed memory (at the cost of maybe 4 more bytes to set up pointers). Zeroing edx would take 2 bytes. The x86-64 System V ABI doesn't guarantee either of these, but Linux's implementation of it does zero (to avoid information-leaks out of the kernel). In a dynamically-linked process, /lib/ld.so runs before _start, and does leave registers non-zero (and probably garbage in memory below the stack pointer).

• I keep -1024 in ebx for use outside of loops. Use bl as a counter for inner loops, ending in zero (which is the low byte of -1024, thus restoring the constant for use outside the loop). Intel Haswell and later don't have partial-register merging penalties for low8 registers (and in fact don't even rename them separately), so there's a dependency on the full register, like on AMD (not a problem here). This would be horrible on Nehalem and earlier, though, which have partial-register stalls when merging. There are other places where I write partial regs and then read the full reg without xor-zeroing or a movzx, usually because I know that some previous code zeroed the upper bytes, and again that's fine on AMD and Intel SnB-family, but slow on Intel pre-Sandybridge.

  I use 1024 as the number of bytes to write to stdout (sub edx, ebx), so my program prints some garbage bytes after the Fibonacci digits, because mov edx, 1000 costs more bytes.

• (not used) adc ebx,ebx with EBX=0 to get EBX=CF, saving 1 byte vs. setc bl.

• dec/jnz inside an adc loop preserves CF without causing a partial-flag stall when adc reads flags on Intel Sandybridge and later. It's bad on earlier CPUs, but AFAIK free on Skylake. Or at worst, an extra uop.

• Use memory below esp as a giant red-zone. Since this is a complete Linux program, I know I didn't install any signal handlers, and that nothing else will asynchronously clobber user-space stack memory. This may not be the case on other OSes.

• Take advantage of the stack-engine to save uop issue bandwidth by using pop eax (1 uop + occasional stack-sync uop) instead of lodsd (2 uops on Haswell/Skylake, 3 on IvB and earlier according to Agner Fog's instruction tables)). IIRC, this dropped the run-time from about 83 seconds to 73. I could probably get the same speed from using a mov with an indexed addressing mode, like mov eax, [edi+ebp] where ebp holds the offset between src and dst buffers. (It would make the code outside the inner loop more complex, having to negate the offset register as part of swapping src and dst for Fibonacci iterations.) See the "performance" section below for more.

• start the sequence by giving the first iteration a carry-in (one byte stc), instead of storing a 1 in memory anywhere. Lots of other problem-specific stuff documented in comments.

NASM listing (machine-code + source), generated with nasm -felf32 fibonacci-1G.asm -l /dev/stdout | cut -b -28,$((28+12))- | sed 's/^/ /'. (Then I hand-removed some blocks of commented stuff, so the line numbering has gaps.) To strip out the leading columns so you can feed it into YASM or NASM, use cut -b 27- <fibonacci-1G.lst > fibonacci-1G.asm.

  1          machine      global _start
  2          code         _start:
  3 address

  4 00000000 B900CA9A3B       mov    ecx, 1000000000       ; Fib(ecx) loop counter
  5                       ;    lea    ebp, [ecx-1]          ;  base-1 in the base(pointer) register ;)
  6 00000005 89CD             mov    ebp, ecx    ; not wrapping on limb==1000000000 doesn't change the result.
  7                                              ; It's either self-correcting after the next add, or shifted out the bottom faster than Fib() grows.
  8                       
 42                       
 43                       ;    mov    esp, buf1
 44                       
 45                       ;    mov    esi, buf1   ; ungolfed: static buffers instead of the stack
 46                       ;    mov    edi, buf2

 47 00000007 BB00FCFFFF       mov    ebx, -1024
 48 0000000C 21DC             and    esp, ebx    ; alignment necessary for convenient pointer-reset
 49                       ;    sar    ebx, 1
 50 0000000E 01DC             add    esp, ebx     ; lea    edi, [esp + ebx].  Can't skip this: ASLR or large environment can put ESP near the bottom of a 1024-byte block to start with
 51 00000010 8D3C1C           lea    edi, [esp + ebx*1]
 52                           ;xchg   esp, edi   ; This is slightly faster.  IDK why.
 53                       
 54                           ; It's ok for EDI to be below ESP by multiple 4k pages.  On Linux, IIRC the main stack automatically extends up to ulimit -s, even if you haven't adjusted ESP.  (Earlier I used -4096 instead of -1024)
 55                           ; After an even number of swaps, EDI will be pointing to the lower-addressed buffer
 56                           ; This allows a small buffer size without having the string step on the number.
 57
 58                       ; registers that are zero at process startup, which we depend on:
 59                       ;    xor   edx, edx
 60                       ;;  we also depend on memory far below initial ESP being zeroed.
 61
 62 00000013 F9               stc    ; starting conditions: both buffers zeroed, but carry-in = 1
 63                       ; starting Fib(0,1)->0,1,1,2,3 vs. Fib(1,0)->1,0,1,1,2 starting "backwards" puts us 1 count behind
 66
 67                       ;;; register usage:
 68                       ;;; eax, esi: scratch for the adc inner loop, and outer loop
 69                       ;;; ebx: -1024.  Low byte is used as the inner-loop limb counter (ending at zero, restoring the low byte of -1024)
 70                       ;;; ecx: outer-loop Fibonacci iteration counter
 71                       ;;; edx: dst read-write offset (for "right shifting" to discard the least-significant limb)
 72                       ;;; edi: dst pointer
 73                       ;;; esp: src pointer
 74                       ;;; ebp: base-1 = 999999999.  Actually still happens to work with ebp=1000000000.
 75
 76                       .fibonacci:
 77                       limbcount equ 114             ; 112 = 1006 decimal digits / 9 digits per limb.  Not enough for 1000 correct digits, but 114 is.
 78                                                     ; 113 would be enough, but we depend on limbcount being even to avoid a sub
 79 00000014 B372             mov    bl, limbcount
 80                       .digits_add:
 81                           ;lodsd                       ; Skylake: 2 uops.  Or  pop rax  with rsp instead of rsi
 82                       ;    mov    eax, [esp]
 83                       ;    lea    esp, [esp+4]   ; adjust ESP without affecting CF.  Alternative, load relative to edi and negate an offset?  Or add esp,4 after adc before cmp
 84 00000016 58               pop    eax
 85 00000017 130417           adc    eax, [edi + edx*1]    ; read from a potentially-offset location (but still store to the front)
 86                        ;; jz .out   ;; Nope, a zero digit in the result doesn't mean the end!  (Although it might in base 10**9 for this problem)
 87
 88                       %if 0   ;; slower version
                          ;; could be even smaller (and 5.3x slower) with a branch on CF: 25% mispredict rate
 89                           mov  esi, eax
 90                           sub  eax, ebp  ; 1000000000 ; sets CF opposite what we need for next iteration
 91                           cmovc eax, esi
 92                           cmc                         ; 1 extra cycle of latency for the loop-carried dependency. 38,075Mc for 100M iters (with stosd).
 93                                                       ; not much worse: the 2c version bottlenecks on the front-end bottleneck
 94                       %else   ;; faster version
 95 0000001A 8DB0003665C4     lea    esi, [eax - 1000000000]
 96 00000020 39C5             cmp    ebp, eax                ; sets CF when (base-1) < eax.  i.e. when eax>=base
 97 00000022 0F42C6           cmovc  eax, esi                ; eax %= base, keeping it in the [0..base) range
 98                       %endif
 99                       
100                       %if 1
101 00000025 AB               stosd                          ; Skylake: 3 uops.  Like add + non-micro-fused store.  32,909Mcycles for 100M iters (with lea/cmp, not sub/cmc)
102                       %else
103                         mov    [edi], eax                ; 31,954Mcycles for 100M iters: faster than STOSD
104                         lea   edi, [edi+4]               ; Replacing this with ADD EDI,4 before the CMP is much slower: 35,083Mcycles for 100M iters
105                       %endif
106                       
107 00000026 FECB             dec    bl                      ; preserves CF.  The resulting partial-flag merge on ADC would be slow on pre-SnB CPUs
108 00000028 75EC             jnz .digits_add
109                           ; bl=0, ebx=-1024
110                           ; esi has its high bit set opposite to CF
111                       .end_innerloop:
112                           ;; after a non-zero carry-out (CF=1): right-shift both buffers by 1 limb, over the course of the next two iterations
113                           ;; next iteration with r8 = 1 and rsi+=4:  read offset from both, write normal.  ends with CF=0
114                           ;; following iter with r8 = 1 and rsi+=0:  read offset from dest, write normal.  ends with CF=0
115                           ;; following iter with r8 = 0 and rsi+=0:  i.e. back to normal, until next carry-out (possible a few iters later)
116                       
117                           ;; rdi = bufX + 4*limbcount
118                           ;; rsi = bufY + 4*limbcount + 4*carry_last_time
119                       
120                       ;    setc   [rdi]
123 0000002A 0F92C2           setc   dl
124 0000002D 8917             mov    [edi], edx ; store the carry-out into an extra limb beyond limbcount
125 0000002F C1E202           shl    edx, 2

139                           ; keep -1024 in ebx.  Using bl for the limb counter leaves bl zero here, so it's back to -1024 (or -2048 or whatever)
142 00000032 89E0             mov    eax, esp   ; test/setnz could work, but only saves a byte if we can somehow avoid the  or dl,al
143 00000034 2404             and    al, 4      ; only works if limbcount is even, otherwise we'd need to subtract limbcount first.

148 00000036 87FC             xchg   edi, esp   ; Fibonacci: dst and src swap
149 00000038 21DC             and    esp, ebx  ; -1024  ; revert to start of buffer, regardless of offset
150 0000003A 21DF             and    edi, ebx  ; -1024
151                       
152 0000003C 01D4             add    esp, edx             ; read offset in src

155                           ;; after adjusting src, so this only affects read-offset in the dst, not src.
156 0000003E 08C2             or    dl, al              ; also set r8d if we had a source offset last time, to handle the 2nd buffer
157                           ;; clears CF for next iter

165 00000040 E2D2             loop .fibonacci  ; Maybe 0.01% slower than dec/jnz overall

169                       to_string:

175                       stringdigits equ 9*limbcount  ; + 18
176                       ;;; edi and esp are pointing to the start of buffers, esp to the one most recently written
177                       ;;;  edi = esp +/- 2048, which is far enough away even in the worst case where they're growing towards each other
178                       ;;;  update: only 1024 apart, so this only works for even iteration-counts, to prevent overlap

180                           ; ecx = 0 from the end of the fib loop
181                           ;and   ebp, 10     ; works because the low byte of 999999999 is 0xff
182 00000042 8D690A           lea    ebp, [ecx+10]         ;mov    ebp, 10
183 00000045 B172             mov    cl, (stringdigits+8)/9
184                       .toascii:  ; slow but only used once, so we don't need a multiplicative inverse to speed up div by 10
185                           ;add   eax, [rsi]    ; eax has the carry from last limb:  0..3  (base 4 * 10**9)
186 00000047 58               pop    eax                  ; lodsd
187 00000048 B309             mov    bl, 9
188                       .toascii_digit:
189 0000004A 99               cdq                         ; edx=0 because eax can't have the high bit set
190 0000004B F7F5             div    ebp                  ; edx=remainder = low digit = 0..9.  eax/=10

197 0000004D 80C230           add    dl, '0'
198                                              ; stosb  ; clobber [rdi], then  inc rdi
199 00000050 4F               dec    edi         ; store digits in MSD-first printing order, working backwards from the end of the string
200 00000051 8817             mov    [edi], dl
201                       
202 00000053 FECB             dec    bl
203 00000055 75F3             jnz  .toascii_digit
204                       
205 00000057 E2EE             loop .toascii
206                       
207                           ; Upper bytes of eax=0 here.  Also AL I think, but that isn't useful
208                           ; ebx = -1024
209 00000059 29DA             sub  edx, ebx   ; edx = 1024 + 0..9 (leading digit).  +0 in the Fib(10**9) case
210                       
211 0000005B B004             mov   al, 4                 ; SYS_write
212 0000005D 8D58FD           lea  ebx, [eax-4 + 1]       ; fd=1
213                           ;mov  ecx, edi               ; buf
214 00000060 8D4F01           lea  ecx, [edi+1]           ; Hard-code for Fib(10**9), which has one leading zero in the highest limb.
215                       ;    shr  edx, 1 ;    for use with edx=2048
216                       ;    mov  edx, 100
217                       ;    mov byte  [ecx+edx-1], 0xa;'\n'  ; count+=1 for newline
218 00000063 CD80             int  0x80                   ; write(1, buf+1, 1024)
219                       
220 00000065 89D8             mov  eax, ebx ; SYS_exit=1
221 00000067 CD80             int  0x80     ; exit(ebx=1)
222                       
  # next byte is 0x69, so size = 0x69 = 105 bytes

There's probably room to golf some more bytes out of this, but I've already spent at least 12 hours on this over 2 days. I don't want to sacrifice speed, even though it's way more than fast enough and there is room to make it smaller in ways that cost speed. Part of my reason for posting is showing how fast I can make a brute-force asm version. If anyone wants to really go for minimum-size but maybe 10x slower (e.g. 1 digit per byte), feel free to copy this as a starting point.

The resulting executable (from yasm -felf32 -Worphan-labels -gdwarf2 fibonacci-1G.asm && ld -melf_i386 -o fibonacci-1G fibonacci-1G.o) is 340B (stripped):

size fibonacci-1G
 text    data     bss     dec     hex filename
  105       0       0     105      69 fibonacci-1G

Performance

The inner adc loop is 10 fused-domain uops on Skylake (+1 stack-sync uop every ~128 bytes), so it can issue at one per ~2.5 cycles on Skylake with optimal front-end throughput (ignoring the stack-sync uops). The critical-path latency is 2 cycles, for the adc->cmp -> next iteration's adc loop-carried dependency chain, so the bottleneck should be the front-end issue limit of ~2.5 cycles per iteration.

adc eax, [edi + edx] is 2 unfused-domain uops for the execution ports: load + ALU. It micro-fuses in the decoders (1 fused-domain uop), but un-laminates in the issue stage to 2 fused-domain uops, because of the indexed addressing mode, even on Haswell/Skylake. I thought it would stay micro-fused, like add eax, [edi + edx] does, but maybe keeping indexed addressing modes micro-fused doesn't work for uops that already have 3 inputs (flags, memory, and destination). When I wrote it, I was thinking it wouldn't have a performance downside, but I was wrong. This way of handling of truncation slows down the inner loop every time, whether edx is 0 or 4.

It would be faster to handle the read-write offset for the dst by offsetting edi and using edx to adjust the store. So adc eax, [edi] / ... / mov [edi+edx], eax / lea edi, [edi+4] instead of stosd. Haswell and later can keep an indexed store micro-fused. (Sandybridge/IvB would unlaminate it, too.)

On Intel Haswell and earlier, adc and cmovc are 2 uops each, with 2c latency. (adc eax, [edi+edx] is still un-laminated on Haswell, and issues as 3 fused-domain uops). Broadwell and later allow 3-input uops for more than just FMA (Haswell), making adc and cmovc (and a couple other things) single-uop instructions, like they have been on AMD for a long time. (This is one reason AMD has done well in extended-precision GMP benchmarks for a long time.) Anyway, Haswell's inner loop should be 12 uops (+1 stack-sync uop occasionally), with a front-end bottleneck of ~3c per iter best-case, ignoring stack-sync uops.

Using pop without a balancing push inside a loop means the loop can't run from the LSD (loop stream detector), and has to be re-read from the uop cache into the IDQ every time. If anything, it's a good thing on Skylake, since a 9 or 10 uop loop doesn't quite issue optimally at 4 uops every cycle. This is probably part of why replacing lodsd with pop helped so much. (The LSD can't lock down the uops because that wouldn't leave room to insert a stack-sync uop.) (BTW, a microcode update disables the LSD entirely on Skylake and Skylake-X to fix an erratum. I measured the above before getting that update.)

I profiled it on Haswell, and found that it runs in 381.31 billion clock cycles (regardless of CPU frequency, since it only uses L1D cache, not memory). Front-end issue throughput was 3.72 fused-domain uops per clock, vs. 3.70 for Skylake. (But of course instructions per cycle was down to 2.42 from 2.87, because adc and cmov are 2 uops on Haswell.)

push to replace stosd probably wouldn't help as much, because adc [esp + edx] would trigger a stack-sync uop every time. And would cost a byte for std so lodsd goes the other direction. (mov [edi], eax / lea edi, [edi+4] to replace stosd is a win, going from 32,909Mcycles for 100M iters to 31,954Mcycles for 100M iters. It seems that stosd decodes as 3 uops, with the store-address/store-data uops not micro-fused, so push + stack-sync uops might still be faster than stosd)

The actual performance of ~322.47 billion cycles for 1G iterations of 114 limbs works out to 2.824 cycles per iteration of the inner loop, for the fast 105B version on Skylake. (See ocperf.py output below). That's slower than I predicted from static analysis, but I was ignoring the overhead of the outer-loop and any stack-sync uops.

Perf counters for branches and branch-misses show that the inner loop mispredicts once per outer loop (on the last iteration, when it's not taken). That also accounts for part of the extra time.

---

I could save code-size by making the inner-most loop have 3-cycle latency for the critical path, using mov esi,eax/sub eax,ebp/cmovc eax, esi/cmc (2+2+3+1 = 8B) instead of lea esi, [eax - 1000000000]/cmp ebp,eax/cmovc (6+2+3 = 11B). The cmov/stosd is off the critical path. (The increment-edi uop of stosd can run separately from the store, so each iteration forks off a short dependency chain.) It used to save another 1B by changing the ebp init instruction from lea ebp, [ecx-1] to mov ebp,eax, but I discovered that having the wrong ebp didn't change the result. This would let a limb be exactly == 1000000000 instead of wrapping and producing a carry, but this error propagates slower than we Fib() grows, so this happens not to change the leading 1k digits of the final result. Also, I think that error can correct itself when we're just adding, since there's room in a limb to hold it without overflow. Even 1G + 1G doesn't overflow a 32-bit integer, so it will eventually percolate upwards or be truncated away.

The 3c latency version is 1 extra uop, so the front-end can issue it at one per 2.75c cycles on Skylake, only slightly faster than the back-end can run it. (On Haswell, it will be 13 uops total since it still uses adc and cmov, and bottleneck on the front-end at 3.25c per iter).

In practice it runs a factor of 1.18 slower on Skylake (3.34 cycles per limb), rather than 3/2.5 = 1.2 that I predicted for replacing the front-end bottleneck with the latency bottleneck from just looking at the inner loop without stack-sync uops. Since the stack-sync uops only hurt the fast version (bottlenecked on the front-end instead of latency), it doesn't take much to explain it. e.g. 3/2.54 = 1.18.

Another factor is that the 3c latency version may detect the mispredict on leaving the inner loop while the critical path is still executing (because the front-end can get ahead of the back-end, letting out-of-order execution run the loop-counter uops), so the effective mispredict penalty is lower. Losing those front-end cycles lets the back-end catch up.

If it wasn't for that, we could maybe speed up the 3c cmc version by using a branch in the outer loop instead of branchless handling of the carry_out -> edx and esp offsets. Branch-prediction + speculative execution for a control dependency instead of a data dependency could let the next iteration start running the adc loop while uops from the previous inner loop were still in flight. In the branchless version, the load addresses in the inner loop have a data dependency on CF from the last adc of the last limb.

The 2c latency inner-loop version bottlenecks on the front-end, so the back-end pretty much keeps up. If the outer-loop code was high-latency, the front-end could get ahead issuing uops from the next iteration of the inner loop. (But in this case the outer-loop stuff has plenty of ILP and no high-latency stuff, so the back-end doesn't have much catching up to do when it starts chewing through uops in the out-of-order scheduler as their inputs become ready).

### Output from a profiled run
$ asm-link -m32 fibonacci-1G.asm && (size fibonacci-1G; echo disas fibonacci-1G) && ocperf.py stat -etask-clock,context-switches:u,cpu-migrations:u,page-faults:u,cycles,instructions,uops_issued.any,uops_executed.thread,uops_executed.stall_cycles -r4  ./fibonacci-1G
+ yasm -felf32 -Worphan-labels -gdwarf2 fibonacci-1G.asm
+ ld -melf_i386 -o fibonacci-1G fibonacci-1G.o
   text    data     bss     dec     hex filename
    106       0       0     106      6a fibonacci-1G
disas fibonacci-1G
perf stat -etask-clock,context-switches:u,cpu-migrations:u,page-faults:u,cycles,instructions,cpu/event=0xe,umask=0x1,name=uops_issued_any/,cpu/event=0xb1,umask=0x1,name=uops_executed_thread/,cpu/event=0xb1,umask=0x1,inv=1,cmask=1,name=uops_executed_stall_cycles/ -r4 ./fibonacci-1G
79523178745546834678293851961971481892555421852343989134530399373432466861825193700509996261365567793324820357232224512262917144562756482594995306121113012554998796395160534597890187005674399468448430345998024199240437534019501148301072342650378414269803983873607842842319964573407827842007677609077777031831857446565362535115028517159633510239906992325954713226703655064824359665868860486271597169163514487885274274355081139091679639073803982428480339801102763705442642850327443647811984518254621305295296333398134831057713701281118511282471363114142083189838025269079177870948022177508596851163638833748474280367371478820799566888075091583722494514375193201625820020005307983098872612570282019075093705542329311070849768547158335856239104506794491200115647629256491445095319046849844170025120865040207790125013561778741996050855583171909053951344689194433130268248133632341904943755992625530254665288381226394336004838495350706477119867692795685487968552076848977417717843758594964253843558791057997424878788358402439890396,�X\�;3�I;ro~.�'��R!q��%��X'B ��      8w��▒Ǫ�
 ... repeated 3 more times, for the 3 more runs we're averaging over
  Note the trailing garbage after the trailing digits.

 Performance counter stats for './fibonacci-1G' (4 runs):

      73438.538349      task-clock:u (msec)       #    1.000 CPUs utilized            ( +-  0.05% )
                 0      context-switches:u        #    0.000 K/sec                  
                 0      cpu-migrations:u          #    0.000 K/sec                  
                 2      page-faults:u             #    0.000 K/sec                    ( +- 11.55% )
   322,467,902,120      cycles:u                  #    4.391 GHz                      ( +-  0.05% )
   924,000,029,608      instructions:u            #    2.87  insn per cycle           ( +-  0.00% )
 1,191,553,612,474      uops_issued_any:u         # 16225.181 M/sec                   ( +-  0.00% )
 1,173,953,974,712      uops_executed_thread:u    # 15985.530 M/sec                   ( +-  0.00% )
     6,011,337,533      uops_executed_stall_cycles:u #   81.855 M/sec                    ( +-  1.27% )

      73.436831004 seconds time elapsed                                          ( +-  0.05% )

( +- x %) is the standard-deviation over the 4 runs for that count. Interesting that it runs such a round number of instructions. That 924 billion is not a coincidence. I guess that the outer loop runs a total of 924 instructions.

uops_issued is a fused-domain count (relevant for front-end issue bandwidth), while uops_executed is an unfused-domain count (number of uops sent to execution ports). Micro-fusion packs 2 unfused-domain uops into one fused-domain uop, but mov-elimination means that some fused-domain uops don't need any execution ports. See the linked question for more about counting uops and fused vs. unfused domain. (Also see Agner Fog's instruction tables and uarch guide, and other useful links in the SO x86 tag wiki).

From another run measuring different things: L1D cache misses are totally insignificant, as expected for reading/writing the same two 456B buffers. The inner-loop branch mispredicts once per outer loop (when it's not-taken to leave the loop). (The total time is higher because the computer wasn't totally idle. Probably the other logical core was active some of the time, and more time was spent in interrupts (since the user-space-measured frequency was farther below 4.400GHz). Or multiple cores were active more of the time, lowering the max turbo. I didn't track cpu_clk_unhalted.one_thread_active to see if HT competition was an issue.)

     ### Another run of the same 105/106B "main" version to check other perf counters
      74510.119941      task-clock:u (msec)       #    1.000 CPUs utilized          
                 0      context-switches:u        #    0.000 K/sec                  
                 0      cpu-migrations:u          #    0.000 K/sec                  
                 2      page-faults:u             #    0.000 K/sec                  
   324,455,912,026      cycles:u                  #    4.355 GHz                    
   924,000,036,632      instructions:u            #    2.85  insn per cycle         
   228,005,015,542      L1-dcache-loads:u         # 3069.535 M/sec
           277,081      L1-dcache-load-misses:u   #    0.00% of all L1-dcache hits
                 0      ld_blocks_partial_address_alias:u #    0.000 K/sec                  
   115,000,030,234      branches:u                # 1543.415 M/sec                  
     1,000,017,804      branch-misses:u           #    0.87% of all branches        

My code may well run in fewer cycles on Ryzen, which can issue 5 uops per cycle (or 6 when some of them are 2-uop instructions, like AVX 256b stuff on Ryzen). I'm not sure what its front-end would do with stosd, which is 3 uops on Ryzen (same as Intel). I think the other instructions in the inner loop are the same latency as Skylake and all single-uop. (Including adc eax, [edi+edx], which is an advantage over Skylake).

---

This could probably be significantly smaller, but maybe 9x slower, if I stored the numbers as 1 decimal digit per byte. Generating carry-out with cmp and adjusting with cmov would work the same, but do 1/9th the work. 2 decimal digits per byte (base-100, not 4-bit BCD with a slow DAA) would also work, and div r8 / add ax, 0x3030 turns a 0-99 byte into two ASCII digits in printing order. But 1 digit per byte doesn't need div at all, just looping and adding 0x30. If I store the bytes in printing order, that would make the 2nd loop really simple.

---

Using 18 or 19 decimal digits per 64-bit integer (in 64-bit mode) would make it run about twice as fast, but cost significant code-size for all the REX prefixes, and for 64-bit constants. 32-bit limbs in 64-bit mode prevents using pop eax instead of lodsd. I could still avoid REX prefixes by using esp as a non-pointer scratch register (swapping the usage of esi and esp), instead of using r8d as an 8th register.

If making a callable-function version, converting to 64-bit and using r8d may be cheaper than saving/restoring rsp. 64-bit also can't use the one-byte dec r32 encoding (since it's a REX prefix). But mostly I ended up using dec bl which is 2 bytes. (Because I have a constant in the upper bytes of ebx, and only use it outside of inner loops, which works because the low byte of the constant is 0x00.)

---

High-performance version

For maximum performance (not code-golf), you'd want to unroll the inner loop so it runs at most 22 iterations, which is a short enough taken/not-taken pattern for the branch-predictors to do well. In my experiments, mov cl, 22 before a .inner: dec cl/jnz .inner loop has very few mispredicts (like 0.05%, far less than one per full run of the inner loop), but mov cl,23 mispredicts from 0.35 to 0.6 times per inner loop. 46 is particularly bad, mispredicting ~1.28 times per inner-loop (128M times for 100M outer-loop iterations). 114 mispredicted exactly once per inner loop, same as I found as part of the Fibonacci loop.

I got curious and tried it, unrolling the inner loop by 6 with a %rep 6 (because that divides 114 evenly). That mostly eliminated branch-misses. I made edx negative and used it as an offset for mov stores, so adc eax,[edi] could stay micro-fused. (And so I could avoid stosd). I pulled the lea to update edi out of the %rep block, so it only does one pointer-update per 6 stores.

I also got rid of all the partial-register stuff in the outer loop, although I don't think that was significant. It may have helped slightly to have CF at end of the outer loop not dependent on the final ADC, so some of the inner-loop uops can get started. The outer-loop code could probably be optimized a bit more, since neg edx was the last thing I did, after replacing xchg with just 2 mov instructions (since I already still had 1), and re-arranging the dep chains along with dropping the 8-bit register stuff.

This is the NASM source of just the Fibonacci loop. It's a drop-in replacement for that section of the original version.

  ;;;; Main loop, optimized for performance, not code-size
%assign unrollfac 6
    mov    bl, limbcount/unrollfac  ; and at the end of the outer loop
    align 32
.fibonacci:
limbcount equ 114             ; 112 = 1006 decimal digits / 9 digits per limb.  Not enough for 1000 correct digits, but 114 is.
                              ; 113 would be enough, but we depend on limbcount being even to avoid a sub
;    align 8
.digits_add:

%assign i 0
%rep unrollfac
    ;lodsd                       ; Skylake: 2 uops.  Or  pop rax  with rsp instead of rsi
;    mov    eax, [esp]
;    lea    esp, [esp+4]   ; adjust ESP without affecting CF.  Alternative, load relative to edi and negate an offset?  Or add esp,4 after adc before cmp
    pop    eax
    adc    eax, [edi+i*4]    ; read from a potentially-offset location (but still store to the front)
 ;; jz .out   ;; Nope, a zero digit in the result doesn't mean the end!  (Although it might in base 10**9 for this problem)

    lea    esi, [eax - 1000000000]
    cmp    ebp, eax                ; sets CF when (base-1) < eax.  i.e. when eax>=base
    cmovc  eax, esi                ; eax %= base, keeping it in the [0..base) range
%if 0
    stosd
%else
  mov    [edi+i*4+edx], eax
%endif
%assign i i+1
%endrep
  lea   edi, [edi+4*unrollfac]

    dec    bl                      ; preserves CF.  The resulting partial-flag merge on ADC would be slow on pre-SnB CPUs
    jnz .digits_add
    ; bl=0, ebx=-1024
    ; esi has its high bit set opposite to CF
.end_innerloop:
    ;; after a non-zero carry-out (CF=1): right-shift both buffers by 1 limb, over the course of the next two iterations
    ;; next iteration with r8 = 1 and rsi+=4:  read offset from both, write normal.  ends with CF=0
    ;; following iter with r8 = 1 and rsi+=0:  read offset from dest, write normal.  ends with CF=0
    ;; following iter with r8 = 0 and rsi+=0:  i.e. back to normal, until next carry-out (possible a few iters later)

    ;; rdi = bufX + 4*limbcount
    ;; rsi = bufY + 4*limbcount + 4*carry_last_time

;    setc   [rdi]
;    mov    dl, dh               ; edx=0.  2c latency on SKL, but DH has been ready for a long time
;    adc    edx,edx    ; edx = CF.  1B shorter than setc dl, but requires edx=0 to start
    setc   al
    movzx  edx, al
    mov    [edi], edx ; store the carry-out into an extra limb beyond limbcount
    shl    edx, 2
    ;; Branching to handle the truncation would break the data-dependency (of pointers) on carry-out from this iteration
    ;;  and let the next iteration start, but we bottleneck on the front-end (9 uops)
    ;;  not the loop-carried dependency of the inner loop (2 cycles for adc->cmp -> flag input of adc next iter)
    ;; Since the pattern isn't perfectly regular, branch mispredicts would hurt us

    ; keep -1024 in ebx.  Using bl for the limb counter leaves bl zero here, so it's back to -1024 (or -2048 or whatever)
    mov    eax, esp
    and    esp, 4               ; only works if limbcount is even, otherwise we'd need to subtract limbcount first.

    and    edi, ebx  ; -1024    ; revert to start of buffer, regardless of offset
    add    edi, edx             ; read offset in next iter's src
    ;; maybe   or edi,edx / and edi, 4 | -1024?  Still 2 uops for the same work
    ;;  setc dil?

    ;; after adjusting src, so this only affects read-offset in the dst, not src.
    or     edx, esp             ; also set r8d if we had a source offset last time, to handle the 2nd buffer
    mov    esp, edi

;    xchg   edi, esp   ; Fibonacci: dst and src swap
    and    eax, ebx  ; -1024

    ;; mov    edi, eax
    ;; add    edi, edx
    lea    edi, [eax+edx]
    neg    edx            ; negated read-write offset used with store instead of load, so adc can micro-fuse

    mov    bl, limbcount/unrollfac
    ;; Last instruction must leave CF clear for next iter
;    loop .fibonacci  ; Maybe 0.01% slower than dec/jnz overall
;    dec ecx
    sub ecx, 1                  ; clear any flag dependencies.  No faster than dec, at least when CF doesn't depend on edx
    jnz .fibonacci

Performance:

 Performance counter stats for './fibonacci-1G-performance' (3 runs):

      62280.632258      task-clock (msec)         #    1.000 CPUs utilized            ( +-  0.07% )
                 0      context-switches:u        #    0.000 K/sec                  
                 0      cpu-migrations:u          #    0.000 K/sec                  
                 3      page-faults:u             #    0.000 K/sec                    ( +- 12.50% )
   273,146,159,432      cycles                    #    4.386 GHz                      ( +-  0.07% )
   757,088,570,818      instructions              #    2.77  insn per cycle           ( +-  0.00% )
   740,135,435,806      uops_issued_any           # 11883.878 M/sec                   ( +-  0.00% )
   966,140,990,513      uops_executed_thread      # 15512.704 M/sec                   ( +-  0.00% )
    75,953,944,528      resource_stalls_any       # 1219.544 M/sec                    ( +-  0.23% )
       741,572,966      idq_uops_not_delivered_core #   11.907 M/sec                    ( +- 54.22% )

      62.279833889 seconds time elapsed                                          ( +-  0.07% )

That's for the same Fib(1G), producing the same output in 62.3 seconds instead of 73 seconds. (273.146G cycles, vs. 322.467G. Since everything hits in L1 cache, core clock cycles is really all we need to look at.)

Note the much lower total uops_issued count, well below the uops_executed count. That means many of them were micro-fused: 1 uop in the fused domain (issue/ROB), but 2 uops in the unfused domain (scheduler / execution units)). And that few were eliminated in the issue/rename stage (like mov register copying, or xor-zeroing, which need to issue but don't need an execution unit). Eliminated uops would unbalance the count the other way.

branch-misses is down to ~400k, from 1G, so unrolling worked. resource_stalls.any is significant now, which means the front-end is not the bottleneck anymore: instead the back-end is getting behind and limiting the front-end. idq_uops_not_delivered.core only counts cycles where the front-end didn't deliver uops, but the back-end wasn't stalled. That's nice and low, indicating few front-end bottlenecks.

---

Fun fact: the python version spends more than half its time dividing by 10 rather than adding. (Replacing the a/=10 with a>>=64 speeds it up by more than a factor of 2, but changes the result because binary truncation != decimal truncation.)

My asm version is of course optimized specifically for this problem-size, with the loop iteration-counts hard coded. Even shifting an arbitrary-precision number will copy it, but my version can just read from an offset for the next two iterations to skip even that.

I profiled the python version (64-bit python2.7 on Arch Linux):

ocperf.py stat -etask-clock,context-switches:u,cpu-migrations:u,page-faults:u,cycles,instructions,uops_issued.any,uops_executed.thread,arith.divider_active,branches,branch-misses,L1-dcache-loads,L1-dcache-load-misses python2.7 ./fibonacci-1G.anders-brute-force.py
795231787455468346782938519619714818925554218523439891345303993734324668618251937005099962613655677933248203572322245122629171445627564825949953061211130125549987963951605345978901870056743994684484303459980241992404375340195011483010723426503784142698039838736078428423199645734078278420076776090777770318318574465653625351150285171596335102399069923259547132267036550648243596658688604862715971691635144878852742743550811390916796390738039824284803398011027637054426428503274436478119845182546213052952963333981348310577137012811185112824713631141420831898380252690791778709480221775085968511636388337484742803673714788207995668880750915837224945143751932016258200200053079830988726125702820190750937055423293110708497685471583358562391045067944912001156476292564914450953190468498441700251208650402077901250135617787419960508555831719090539513446891944331302682481336323419049437559926255302546652883812263943360048384953507064771198676927956854879685520768489774177178437585949642538435587910579974100118580

 Performance counter stats for 'python2.7 ./fibonacci-1G.anders-brute-force.py':

     755380.697069      task-clock:u (msec)       #    1.000 CPUs utilized          
                 0      context-switches:u        #    0.000 K/sec                  
                 0      cpu-migrations:u          #    0.000 K/sec                  
               793      page-faults:u             #    0.001 K/sec                  
 3,314,554,673,632      cycles:u                  #    4.388 GHz                      (55.56%)
 4,850,161,993,949      instructions:u            #    1.46  insn per cycle           (66.67%)
 6,741,894,323,711      uops_issued_any:u         # 8925.161 M/sec                    (66.67%)
 7,052,005,073,018      uops_executed_thread:u    # 9335.697 M/sec                    (66.67%)
   425,094,740,110      arith_divider_active:u    #  562.756 M/sec                    (66.67%)
   807,102,521,665      branches:u                # 1068.471 M/sec                    (66.67%)
     4,460,765,466      branch-misses:u           #    0.55% of all branches          (44.44%)
 1,317,454,116,902      L1-dcache-loads:u         # 1744.093 M/sec                    (44.44%)
        36,822,513      L1-dcache-load-misses:u   #    0.00% of all L1-dcache hits    (44.44%)

     755.355560032 seconds time elapsed

Numbers in (parens) are how much of the time that perf counter was being sampled. When looking at more counters than the HW supports, perf rotates between different counters and extrapolates. That's totally fine for a long run of the same task.

If I ran perf after setting sysctl kernel.perf_event_paranoid = 0 (or running perf as root), it would measure 4.400GHz. cycles:u doesn't count time spent in interrupts (or system calls), only user-space cycles. My desktop was almost totally idle, but this is typical.

Answer 4

Haskell, 83 61 bytes

p(a,b)(c,d)=(a*d+b*c-a*c,a*c+b*d)
t g=g.g.g
t(t$t=<<t.p)(1,1)

Outputs (F_1000000000,F_1000000001). On my laptop, it correctly prints the left paren and the first 1000 digits within 133 seconds, using 1.35 GiB of memory.

How it works

The Fibonacci recurrence can be solved using matrix exponentiation:

[F_{i − 1}, F_i; F_i, F_{i + 1}] = [0, 1; 1, 1]ⁱ,

from which we derive these identities:

[F_{i + j − 1}, F_{i + j}; F_{i + j}, F_{i + j + 1}] = [F_{i − 1}, F_i; F_i, F_{i + 1}] ⋅ [F_{j − 1}, F_j; F_j, F_{j + 1}],
F_{i + j} = F_{i + 1}F_{j + 1} − F_{i − 1}F_{j − 1} = F_{i + 1}F_{j + 1} − (F_{i + 1} − F_i)(F_{j + 1} − F_j),
F_{i + j + 1} = F_iF_j + F_{i + 1}F_{j + 1}.

The p function computes (F_{i + j}, F_{i + j + 1}) given (F_i, F_{i + 1}) and (F_j, F_{j + 1}). Writing f n for (F_i, F_{i + 1}), we have p (f i) (f j) = f (i + j).

Then,

(t=<<t.p) (f i)
= t ((t.p) (f i)) (f i)
= t (p (f i).p (f i).p (f i)) (f i)
= (p (f i).p (f i).p (f i).p (f i).p (f i).p (f i).p (f i).p (f i).p (f i)) (f i)
= f (10 * i),

(t$t=<<t.p) (f i)
= ((t=<<t.p).(t=<<t.p).(t=<<t.p)) (f i)
= f (10^3 * i),

t(t$t=<<t.p) (f i)
= ((t$t=<<t.p).(t$t=<<t.p).(t$t=<<t.p)) (f i)
= f (10^9 * i),

and we plug in f 1 = (1,1).

Answer 5

Mathematica, 15 34 bytes

Fibonacci itself takes ~6s on my computer. And 95(+/-5)s for frontend to display it.

Fibonacci@1*^9&

The first 1000 digits (34 bytes): ⌊Fibonacci@1*^9/1*^208986640⌋&

Longer but faster ToString@Fibonacci@1*^9~StringTake~1000&:

Answer 6

Python 2, 70 bytes

a,b=0,1
i=1e9
while i:
 a,b=b,a+b;i-=1
 if a>>3360:a/=10;b/=10
print a

This ran in 18 minutes and 31 seconds on my laptop, producing the correct 1000 digits followed by 74100118580 (the correct following digits are 74248787892).

Answer 7

Haskell, 78 bytes

(a%b)n|n<1=b|odd n=b%(a+b)$n-1|r<-2*a*b-a*a=r%(a*a+b*b)$div n 2
1%0$2143923439

Try it online!

Took 48 seconds on TIO. Same recursive formula as my Python answer, but without truncating.

The constant 2143923439 is 10**9-1, reversed in binary, and with an extra 1 at the end. Iterating through its binary digits in reverse simulates iterating through the binary digits of 10**9-1. It seems shorter to hardcode this than to compute it.

Answer 8

Haskell, 202 184 174 173 170 168 164 162 bytes

(a,b)!(c,d)=a*c+b*d
l x=((34,55)!x,(55,89)!x)
f(a,b)|x<-l(a,b)=(x!l(b-a,a),x!x)
r=l.f
k=f.f.f
j=f.r.r.r.r
main=print$take 1000$show$fst$f$r$k$k$r$k$j$f$r$j$r(0,1)

Try it online!

Explanation

This uses a rather fast way to calculate fibonacci numbers. The function l takes two fibonacci numbers and calculates the fibonacci numbers 10 later, while f takes the nth and n+1th fibonacci numbers and calculates the 2n+20th and 2n+21th fibonacci numbers. I chain them rather haphazardly to get 1 billion and grab the first 1000 digits.

Answer 9

Haskell, 81 bytes

f n|n<3=1|even n=fk*(2*f(k+1)-fk)|1>0=f(k+1)^2+fk^2 where k=n`div`2;fk=f k
f$10^9

Explanation

f n recursively computes the nth fibonacci number using the recurrence from xnor's answer with common-subexpression elimination. Unlike the other solutions which have been posted, which use O(log(n)) multiplications, we have a O(log(n))-depth recursion with a branching factor of 2, for a complexity of O(n) multiplications.

However, all is not lost! Because almost all calls will be near the bottom of the recursion tree, we can use fast native arithmetic where possible and avoid lots of manipulation of huge bignums. It spits out an answer in a couple of minutes on my box.

Answer 10

T-SQL, 422 414 453 bytes (Verified, now competing!)

EDIT 2: Changed to INT BIGINT DECIMAL(37,0), Gained a few bytes but increased speed enough to complete to 1 billion! Completed in 45 hours 29 minutes, verifies against the given string, and displays an additional 8 characters (which may or may not be right due to rounding errors).

T-SQL has no native "huge number" support, so had to roll my own text-based huge number adder using 1008-character strings:

DECLARE @a char(1008)=REPLICATE('0',1008),@ char(1008)=REPLICATE('0',1007)+'1',@c varchar(max),@x bigint=1,@y int,@t varchar(37),@f int=0o:SELECT @x+=1,@c='',@y=1i:SELECT @t=CONVERT(DECIMAL(37,0),RIGHT(@a,36))+CONVERT(DECIMAL(37,0),RIGHT(@,36))+@f,@a=RIGHT(@a,36)+@a,@=RIGHT(@,36)+@,@c=RIGHT(REPLICATE('0',36)+@t,36)+@c,@y+=1IF LEN(@t)>36SET @f=1 ELSE SET @f=0IF @y<29GOTO i
IF @f=1SELECT @a='0'+@,@='1'+@c ELSE SELECT @a=@,@=@c
If @x<1e9 GOTO o
PRINT @

Here's the formatted version with comments:

DECLARE @a char(1008)=REPLICATE('0',1008)       --fib(a), have to manually fill
       ,@ char(1008)=REPLICATE('0',1007)+'1'    --fib(b), shortened variable
       ,@c varchar(max), @x bigint=1, @y int, @t varchar(37), @f int=0
o:  --outer loop
    SELECT @x+=1, @c='', @y=1
    i:  --inner loop
        SELECT @t=CONVERT(DECIMAL(37,0),RIGHT(@a,36))      --adds last chunk of string
                 +CONVERT(DECIMAL(37,0),RIGHT(@,36)) + @f
              ,@a=RIGHT(@a,36)+@a                          --"rotates" the strings
              ,@=RIGHT(@,36)+@
              ,@c=RIGHT(REPLICATE('0',36)+@t,36)+@c        --combines result
              ,@y+=1
        IF LEN(@t)>36 SET @f=1 ELSE SET @f=0               --flag for carrying the 1
     IF @y<29 GOTO i                                       --28 * 36 digits = 1008 places
     IF @f=1 SELECT @a='0'+@, @='1'+@c                     --manually carries the 1
        ELSE SELECT @a=@, @=@c
If @x<1e9 GOTO o
PRINT @

Basically I'm manually manipulating 1008-character zero-filled strings representing my two Fibonacci variables, @a and @.

I add them 8 18 36 digits at a time, by stripping off the last 36 digits, converting to a manageable numeric type (DECIMAL(37,0)), adding them up, then smashing it back into another long string @c. I then "rotate" @a and @ by moving the last 36 digits to the front, and repeating the process. 28 rotations * 36 digits covers all 1008. I have to "carry the one" manually.

Once our number starts to exceed my string length, I "shift left" and we start to lose some precision, but the error is well within my extra characters.

I tried using a SQL table full of INTs and BIGINTs, with similar logic, and it was dramatically slower. Weird.

Answer 11

PARI/GP, 45 bytes

\p1100
s=sqrt(5)
((1+s)/2)^1e9/s/1e208986640

Somehow \p1000 isn't enough. This doesn't work with 32 bit systems. The final division is to avoid the decimal point in scientific notation.

Answer 12

Pari/GP, 15 + 5 = 20 bytes

fibonacci(10^9)

Run with the command line option -s1g to allocate 1 Gbytes of memory.

Answer 13

Ruby, 63 bytes

man, I'm bad at golfing ruby; but the BigInt class does wonders for this kind of stuff. We use the same algorithm as Anders Kaseorg.

require 'matrix'
m=Matrix
puts m[[1,1],[1,0]]**10**9*m[[1],[1]]