11 = (1+2+3+4+5) - (1+2+3) + (6) - (4)

Question

Given a positive integer N, your task is to return the number of steps required by the following algorithm to reach N:

1. Find the smallest triangular number T_i such that T_i ≥ N. Build the corresponding list L = [ 1, 2, ..., i ].

2. While the sum of the terms of L is greater than N, remove the first term from the list.

3. If the sum of the terms of L is now less than N, increment i and append it to the list. Go on with step #2.

We stop as soon as N is reached. Only the first step is systematically executed. Steps #2 and #3 may not be processed at all.

Examples

Below is an example for N = 11:

So the expected output for N = 11 is 4.

Other examples:

• N = 5 - We start with T₃ = 1 + 2 + 3 = 6, followed by 2 + 3 = 5. Expected output: 2.
• N = 10 - Only the first step is required because 10 is a triangular number: T₄ = 1 + 2 + 3 + 4 = 10. Expected output: 1.

First 100 values

Below are the results for 1 ≤ N ≤ 100:

  1,  2,  1,  4,  2,  1,  2, 10,  2,  1,  4,  2,  6,  2,  1, 22,  8,  2, 10,  2,
  1,  2, 12,  6,  2,  4,  2,  1, 16,  2, 18, 50,  2,  6,  2,  1, 22,  6,  2,  4,
 26,  2, 28,  2,  1,  8, 30, 16,  2,  6,  4,  2, 36,  2,  1,  2,  4, 12, 40,  2,
 42, 14,  2,108,  2,  1, 46,  2,  6,  4, 50,  2, 52, 18,  2,  4,  2,  1, 56, 12,
  2, 20, 60,  4,  2, 22, 10,  2, 66,  2,  1,  4, 10, 24,  2, 40, 72,  8,  2,  6

Rules

• You may write either a full program or a function, that either prints or returns the result.
• You're required to process any N ≤ 65536 in less than one minute on mid-range hardware.
• Given enough time, your program/function should theoretically work for any value of N that is natively supported by your language. If it doesn't, please explain why in your answer.
• This is code golf, so the shortest answer in bytes wins!

Answer 1

Jelly, 29 31 bytes

ÆDµ’H+Ṛ%1$ÐḟṂ
>TḢ_@Ç}‘Ḥ
R+\ðċȯç

A monadic link that returns the result (N=65536 takes less than two seconds).

Try it online!

How?

For a thorough explanation of the algorithm see the fantastic post by Martin Ender.

ÆDµ’H+Ṛ%1$ÐḟṂ - Link 1, smallest natural number, M, that satisfies the below*, N
              - * N = T(M) - T(i) for some non-negative integer i <= M
ÆD            - divisors of N
  µ           - monadic chain separation, call that d
   ’          - increment d (vectorises)
    H         - halve (vectorises
      Ṛ       - reverse d
     +        - add (vectorises)
          Ðḟ  - filter discard if:
       %1$    -   modulo one is truthy (those which are the result of even divisors)
            Ṃ - minimum

>TḢ_@Ç}‘Ḥ - Link 2, evaluate result for non-triangular: list of T(1) to T(N), N
>         - T(i) > N
 T        - truthy indexes
  Ḣ       - head (yields the first i for which T(i) > N)
     Ç}   - call last link (1) as a monad converted to a dyad using the right argument
   _@     - subtract with reverse @rguments
       ‘  - increment
        Ḥ - double 

R+\ðċȯç - Main link: N
R       - range -> [1,2,...,N]
 +\     - reduce with addition -> [1,3,6,10,...T(N)]
   ð    - dyadic chain separation, call that t
    ċ   - count occurrences of N in t (1 if N is triangular else 0)
      ç - call last link (2) as a dyad(t, N)
     ȯ  - or

---

The 29 byte full-program implementation I created of the algorithm described takes 4 min 30 for N=65536 on my laptop, so I suppose it does not count.

Ṁ‘ṭµS<³µ¿
ḊµS>³µ¿
0®Ḃ‘©¤ĿÐĿL’

Using a while loop for every step 3 and reusing it as step 1 is equal in length to what I can manage with initialising the list since no check on step 3 means building a list until nothing remains and then finding the first index of the value:

ḊµS>³µ¿
Ṁ‘ṭ
Ḥ½_.ĊR®Ḃ‘©¤ĿÐĿS€i

Answer 2

Mathematica, 79 bytes

Min[2#/(d=Divisors@#~Cases~_?OddQ)+d]-2⌊(2#)^.5+.5⌋+⌈Sqrt[8#+1]~Mod~1⌉&

Explanation

I couldn't be bothered to implement the algorithm in the challenge, so I wanted to look for a shortcut to the solution. While I found one, unfortunately it doesn't beat the Mathematica answer that does implement the algorithm. That said, I'm sure this isn't optimally golfed yet, and there might be other languages who can benefit from this approach or some of the insights gained in the process.

So I claim that the sequence we're supposed to compute is:

f(n) = 2*(A212652(n) - A002024(n)) + 1 + A023532(n-1)

Alternatively, it's f(n) = 1 if n is a triangular number and f(n) = 2*(A212652(n) - A002024(n) + 1) otherwise.

In the first expression, A023532 simply encodes these two different cases. The other two sequences (plus 1) are the difference between the the largest integer k in the longest decomposition of n into consecutive integers (k-i+1) + (k-i+2) + ... + k = n and the largest integer j so that 1 + 2 + ... + j < n.

In somewhat simpler words, here is how we find the answer for non-triangular numbers: first, find the largest triangular number T_j which is less than n. Then j is the penultimate integer that gets added during step 1 (because after adding j+1 we will have exceeded n). Then decompose n into as many (or as small) consecutive integers as possible and call the maximum among these numbers k. The result is simply 2*(k-j). The intuitive reason for this is that the maximum in the decomposition grows by 1 every other step and we stop when we reach k.

We need to show four things to prove that this works:

1. f(n) = 1 for triangular numbers. This is trivially the case, because the first step simply iterates through all triangular numbers. If we hit n exactly during this process we're done and there was only one step to compute.
2. For all other numbers, we always end after a deletion step, never after an insertion step. That means all other f(n) are even.
3. In each insertion step after the first, we only add a single number. This guarantees that we'll reach a decomposition including k after k-j pairs of steps.
4. The final decomposition of n that we obtain is always the longest possible decomposition of n into consecutive integers, or in other words, it's always the decomposition of n with the lowest maximum among the summed numbers. In other words, the last number we add to the sum is always A212652(n).

We've already shown why (1) is true. Next, we prove that we can't end on an insertion step except the initial one (which doesn't happen for non-triangular numbers).

Suppose we ended on an insertion step, reaching n after adding a value p to the sum. That means that before this insertion step, the value was n-p (or less if we added multiple values at once). But this insertion step was preceded by a deletion step (since we couldn't have hit n during step 1). The last value q we removed during this deletion step was necessarily less than p due to the way the algorithm works. But that means before we removed q we had n-p+q (or less) which is less than n. But that's a contradiction, because we would have had to stop removing integers when we hit n-p+q instead of removing another q. This proves point (2) above. So now we know that we always end on a deletion step and that therefore all non-triangular numbers have even outputs.

Next we prove (3), that each insertion step can only insert one value. This is essentially a corollary of (2). We have shown that after adding one value we cannot hit n exactly and since the prove was using an inequality, we also cannot end up below n (since then n-p+q would still be less than n and we shouldn't have removed that many values in the first place). So whenever we add a single value, we're guaranteed to exceed n because we went below n by removing a smaller value. Hence, we know that the upper end of the sum grows by 1 every other step. We know the initial value of this upper end (it's the smallest m such that T_m > n). Now we just need to figure out this upper end once we've reached the final sum. Then the number of steps is simply twice the difference (plus 1).

To do this, we prove (4), that the final sum is always the decomposition of n into as many integers as possible, or the decomposition where the maximum in that decomposition is minimal (i.e. it's the earliest possible decomposition). We'll again do this by contradiction (the wording in this part could be a bit more rigorous, but I've already spent way too much time on this...).

Say the earliest/longest possible decomposition of n is some a + (a+1) + ... (b-1) + b, a ≤ b, and say the algorithm skips it. That means at the time that b gets added, a must no longer be part of the sum. If a was part of the sum s, then we'd have n ≤ s at that moment. So either the sum only contains the values from a to b, which equals n and we stop (hence we didn't skip this decomposition), or there is at least one value less than a in the sum, win which case n < s and that value would get removed until we hit the exact sum (again, the decomposition wasn't skipped). So we'd have to get rid of a before adding b. But that means we'd have to reach a situation in which a is the smallest component of the sum, and the largest isn't b yet. However, at that point we can't remove a, because the sum is clearly less than n (since b is missing), so we're required to add values first until we add b and hit n exactly. This proves (4).

So taking these things together: we know that the first pair of steps gives us a maximum value of A002024(n). We know that the maximum value of the final decomposition is A212652(n). And we know that this maximum is incremented once in every pair of steps. Hence, the final expression is 2*(A212652(n) - A002024(n) + 1). This formula almost works for triangular numbers, except that for those we only need 1 step instead of 2, which is why we correct the result with the indicator function of the triangular numbers (or its inverse, whichever is more convenient).

Finally, as for the implementation. For the former sequence, I'm using the formula MIN(odd d|n; n/d + (d-1)/2) from OEIS. It turns out to save a few bytes if we take the factor of 2 into this expression to get MIN(odd d|n; 2n/d + d-1), because that -1 then cancels with the +1 in my first version of f(n) which directly encodes the two cases for triangular and non-triangular numbers. In the code, this is:

Min[2#/(d=Divisors@#~Cases~_?OddQ)+d]

For the latter sequence (1, 2, 2, 3, 3, 3, ...), we can use a simple closed form:

⌊(2#)^.5+.5⌋

And finally, the inverse indicator function of the triangular numbers is 0 whenever 8n+1 is a perfect square. This can be expressed in Mathematica as

⌈Sqrt[8#+1]~Mod~1⌉

There are a lot of ways to express these last two sequences and to shift some constant offset between them, so I'm sure this is not an optimal implementation yet, but I hope this might give others a starting point to look into new approaches in their own languages.

Since I went to all this trouble, here is a plot of the sequence up to n = 1000 (I could also compute 100k in a couple of seconds, but it doesn't really show any additional insights):

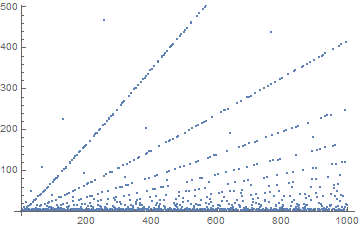
It might be interesting to look into the variations about those very straight lines, but I'll leave that to someone else...

Answer 3

Mathematica, 72 bytes

(For[l=u=c=k=0,k!=#,c++,If[#>k,While[#>k,k+=++u],While[#<k,k-=l++]]];c)&

Pure function taking an integer argument.

How it works

For[ ... ]

A For loop.

l=u=c=k=0

Initialization; set l (lower), u (upper), c (counter), and k (sum) to 0.

k!=#

Condition; repeat while k is not equal to the input.

c++

Increment; increment the counter c.

If[#>k,For[,#>k,,k+=++u],For[,#<k,,k-=l++]]

Body

If[#>k, ... ]

If the input is greater than k:

While[#>k,k+=++u]

While the input is greater than k, increment u and increment k by u.

If the input is not greater than k:

While[#<k,k-=l++]

While the input is less than k, decrement k by l and increment l.

( ... ;c)

Return c after the loop.

Answer 4

Haskell, 70 63 68 64 bytes

EDIT:

• -7 bytes: Got rid of a space, two signs, and some parentheses by negating the sense of a. Fixed off-by-one errors in the explanation.
• +5 bytes: Argh, completely missed that 65536 requirement, and it turns out (1) powers of 2 are particularly expensive, because they only get hit when you get to the number itself (2) so is summing long ranges (that wrap around zero) all the time. Replaced the sum with a mathematical formula.
• -4 bytes: Adjusted a and b linearly to get terms in the summation formula to cancel.

1#1 is an anonymous function taking and returning an integer.

Use as (1#1) 100.

1#1
(a#b)n|s<-a*a-b*b=sum$[a#(b+2)$n|s>8*n]++[(b#a)(-n)+1|s<8*n]

Try it online!

How it works

• (a#b)n represents the current step of calculation. a, b are numbers in 1, 3, 5, .., while n can be either positive or negative depending on the step.
  • When in step 1 or 3, it represents the list [(a+1)/2,(a+3)/2..(b-1)/2] and goal number -n.
  • When in step 2, it represents the list [(b+1)/2,(b+3)/2..(a-1)/2] and goal number n.
• The strange correspondence between a, b and the lists is in order to be able to do summation with the short expression s=a*a-b*b.
  • In step 1 and 3, this is the same as s= -8*sum[(a+1)/2..(b-1)/2].
  • In step 2, this is the same as s=8*sum[(b+1)/2..(a-1)/2].
• Branching is done by having list comprehensions that produce elements in only one case each, and summing the results.
  • If s>8*n, then b is incremented by 2 before recursing.
    • In step 1 and 3, this grows the list, while in step 2, this shrinks it.
  • If s<8*n, then recursion changes the step by swapping a and b, and negating n, and 1 is added to the result.
  • If s==8*n, then neither of the two list comprehensions gives any elements, so the sum is 0.
• (1#1) n represents a dummy "stage 2" before starting, that immediately gets changed to step 1, building the list from [1..0]=[].

Answer 5

Python 2, 104 bytes

N=input();i=s=0;l=()
while N!=sum(l):exec'while sum(l)'+['<N:i+=1;l+=i,','>N:l=l[1:]'][s%2];s+=1
print s

Try it online!

Alternates between adding terms to the end of the list, and removing terms from the beginning.

Answer 6

PHP>=7.0, 74 Bytes

while($i=$r<=>$argn)for($s++;($r<=>$argn)==$i;)$r+=$i+1?-++$y:++$x;echo$s;

use the spaceship operator

Try it online!

Expanded

while($i=$r<=>$argn) # if input is not equal sum of array
  for($s++;  # raise count steps
  ($r<=>$argn)==$i;)
  # so long as value compare to input has not change to lower/higher to higher/lower or equal  
    $r+=$i+1
      ?-++$y # if $i was higher remove the first integer
      :++$x;} # if $i was lower add the next highest integer     
echo$s; # Output steps

Answer 7

C, 94 91 bytes

Try Online

c;s;m;M;f(n){while(s-n){while(s<n)s+=++M;c++;if(s==n)break;while(s>n)s-=++m;c++;}return c;}

Answer 8

Python 3, 150 138 bytes

n=int(input())
S=sum
l=[1]
i=s=1
while S(l)<n:i+=1;l+=[i]
while S(l)!=n:
 while S(l)>n:l.pop(0)
 s+=1
 if S(l)<n:i+=1;l+=[i];s+=1
print(s)

Changelog:

• Changed append to +=, removed else (thanks musicman523, Loovjo; -12 bytes)

Answer 9

JavaScript (ES6), 82 bytes

D=(o,a=0,b=1,d=1,c=0)=>a<o?D(o,a+=b,b+1,d,c+(a>=o)):a>o?D(o,a-=d,b,d+1,c+(a<=o)):c

Test Snippet

D=(o,a=0,b=1,d=1,c=0)=>a<o?D(o,a+=b,b+1,d,c+(a>=o)):a>o?D(o,a-=d,b,d+1,c+(a<=o)):c

<input type="number" oninput="o.textContent=D(this.value)"></input>
<pre id='o'></pre>

Answer 10

dc, 61 bytes

dsN[ddd9k4*d2*1+dv-0k2/-d1+*2/-d[q]s.0=.-lN-0lN-sNlFx]dsFxz2-

Try it online!

Explanation

Main recursive macro:

ddd9k4*d2*1+dv-0k2/-d1+*2/-d[q]s.0=.-lN-0lN-sNlFx
   9k4*d2*1+dv-0k2/-                              # Compute triangular root
                    d1+*2/                        # Compute triangular number
  d                       -d[q]s.0=.              # Check if sum is exact
 d                                  -lN-          # Compute S-N or S+N
                                        0lN-sN    # Update N := -N
d                                             lFx # Leave the trail and recurse

This macro:

1. Finds minimum triangular number that exceeds the current number on the stack (using the modified triangular root formula).
2. Checks if triangular sum S represents the current number exactly. Exits if it does.
3. Proceeds to step 1 with either S+N (over-approximation) or S-N (under-approximation), the choice alternates between iterations.

When it does exit, the trail left on the stack tells the main program how many iterations it took.

Answer 11

Python 2, 86 81 bytes

n=input()
l=u=i=s=0
while n:k=n>0;i+=k^s;s=k;l+=k;n-=l*k;u+=k^1;n+=u*-~-k
print i

Try it online!

Computes the 65536 test case in 0.183s on TIO.

---

This recursive version at 84 bytes is not able to compute all values up to 65536:

def f(n,l=[0],m=1):k=n>sum(l);return n==sum(l)or f(n,[l[1:],l+[l[-1]+1]][k],k)+(m^k)

Try it online!

Answer 12

Batch, 126 bytes

@echo off
set/an=s=l=u=0
:l
if %s% lss %1 set/as+=u+=1,n+=!!l&goto l
if %s% gtr %1 set/as-=l+=1&goto l
cmd/cset/an+n+2-!l

Explanation: l is zero if step 2 has never executed. This allows n to track number of iterations of step 3. Since the algorithm never stops at step 3, it must therefore have run step 1 once and step 2 n+1 times for a total of n+n+2 steps. However if the parameter is a triangular number then step 2 never executes so we need to subtract one step.

Answer 13

Mathematica, 92 bytes

(For[q=a=b=0;t={},t~AppendTo~q;q!=#,If[q<#,q+=++b,q-=++a]];Length@Split@Sign@Differences@t)&

Pure function taking an integer argument and returning an integer.

The variables a and b stand for the (constantly changing) beginning and end numbers in the sum under consideration, while q stands for the running total (of the numbers from a+1 to b); t keeps track of all the values of q encountered so far. After initializing these variables, the For loop keeps executing If[q<#,q+=++b,q-=++a], which either adds a new number on to the end or subtracts the number at the front as dictated by the spec, until q equals the input.

Now we just have to extract the number of steps from t, the list of q values encountered along the way. For example, when the input is 11, the For loop exits with t equaling {0,1,3,6,10,15,14,12,9,15,11}. The best way I found to calculate the number of steps from this is to count how many times the differences switch from going up to going down; that's what the verbose command Length@Split@Sign@Differences@t does, but I suspect that can be improved.

Answer 14

C (tcc), 71 bytes (61+10)

Command-line arguments (including a space):

-Dw=while

Source:

c,m,M,s;f(n){w(++c,s-n){w(c&s<n)s+=++M;w(~c&s>n)s-=m++;}--c;}

How it works:

c counts the number of steps. m and M store the minimum and maximum of the range, s the sum. Initially, they're all zero.

Continuously, c is increased, and s is compared to n. As long as they're unequal:

• If c is odd, then as long as s<n, add an integer to the end of the range: increase M by one, and s by M.

• If c is even, then as long as s>n, remove an integer from the start of the range: decrease s by m, and increase m by one.

When the loop exits, c has been increased one too many times. Decrementing it produces the correct result, and it happens to be calculated in the correct register to act as the return value.

Amusingly happens to use the exact same variable names as Khaled.K's C answer. They aren't copied.

Answer 15

Perl 6, 114 bytes

{((0,0,1),->(\a,\b,\c){b,(a..*).first(->\d{(d,b).minmax.sum*c>=$_*c}),-c}...->(\a,\b,\c){(a,b).minmax.sum==$_})-1}

(inspired by an earlier Haskell implementation)

Try it
It runs with an input of 65536 in under 45 seconds on my computer, but I have been unable to get it to run in under 60 seconds with TIO.run.
I have Rakudo v2017.04+ , where it has v2017.01.
Rakudo/NQP/MoarVM gets optimizations almost daily, so there could be any number of them from the interim that are needed to get it in under time.

---

Expanded

{
  (

    # generate a sequence

    (0,0,1),           # initial value 

    -> (\a,\b,\c) {
      b,               # swap the first two values

      (a..*)
      .first(          # find the first number that brings us to or past the input

        -> \d {
          (d,b).minmax # get a Range object regardless of which is larger
          .sum * c     # sum it, and negate it every other time

          >=           # is it equal to or greater than

          $_ * c       # negate the original input every other time
        }

      ),

      -c               # invert for next round
    }

    ...                # keep doing that until

    -> (\a,\b,\c) {
     (a,b).minmax.sum == $_ # it finally reaches the input
    }

  ) - 1 # count the number of elements in the sequence
        # and subtract one for the initializer
}

Note that Rakudo has an optimization for Range.sum so that it doesn't have to iterate through all of the values.