51
6
Consider the positive integer powers of five in decimal. Here are the first 25, right aligned:
X 5^X
1 5
2 25
3 125
4 625
5 3125
6 15625
7 78125
8 390625
9 1953125
10 9765625
11 48828125
12 244140625
13 1220703125
14 6103515625
15 30517578125
16 152587890625
17 762939453125
18 3814697265625
19 19073486328125
20 95367431640625
21 476837158203125
22 2384185791015625
23 11920928955078125
24 59604644775390625
25 298023223876953125
Notice that the rightmost column of the powers is all 5's. The second column from the right is all 2's. The third column from the right, read from top to bottom, alternates 1, 6, 1, 6, etc. The next column starts 3, 5, 8, 0 and then cycles.
In fact, every column (if we go down far enough) has a cycling sequence of digits whose length is twice that of the previous cycle, except for the initial 5's and 2's cycles.
Calling N the column number, starting with N = 1 at the right, the first few cycles are:
N cycle at column N
1 5
2 2
3 16
4 3580
5 17956240
6 3978175584236200
7 19840377976181556439582242163600
8 4420183983595778219796176036355599756384380402237642416215818000
Challenge
Given a positive integer N, output the decimal digits of the cycle at column N, as described above. For example, the output for N = 4 would be 3580.
The digits may be output as a list such as [3, 5, 8, 0] or in another reasonable format so long as:
- The digits are in order as read from top to bottom in the power columns. e.g.
0853is invalid. - The cycle starts with the top number in its power column. e.g.
5803is invalid as the 4th column starts with3not5. - Exactly one cycle is output. e.g.
358or35803or35803580would all be invalid.
Your code must work for at least N = 1 through 30.
If desired you may assume the columns are 0-indexed instead of 1-indexed. So N = 0 gives 5, N = 1 gives 2, N = 2 gives 16, N = 3 gives 3580, etc.
The shortest code in bytes wins.
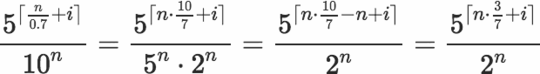
The order makes this quite tricky. – Dennis – 2017-02-25T05:35:31.480
9The cycle length is always
2^(N-2)exceptN = 1– JungHwan Min – 2017-02-25T05:36:38.8571
Can approximations be used? The output is valid until N=72, which would theoretically print 2.36E+21 digits.
– JungHwan Min – 2017-02-25T08:02:34.020Is this sequence in the OEIS? – StarWeaver – 2017-02-26T15:16:28.983
@StarWeaver Nope. – Mego – 2017-06-10T11:49:17.260