Zig-zag lemma

In mathematics, particularly homological algebra, the zig-zag lemma asserts the existence of a particular long exact sequence in the homology groups of certain chain complexes. The result is valid in every abelian category.

Statement

In an abelian category (such as the category of abelian groups or the category of vector spaces over a given field), let ${\displaystyle ({\mathcal {A}},\partial _{\bullet }),({\mathcal {B}},\partial _{\bullet }')}$ and ${\displaystyle ({\mathcal {C}},\partial _{\bullet }'')}$ be chain complexes that fit into the following short exact sequence:

${\displaystyle 0\longrightarrow {\mathcal {A}}{\stackrel {\alpha }{\longrightarrow }}{\mathcal {B}}{\stackrel {\beta }{\longrightarrow }}{\mathcal {C}}\longrightarrow 0}$

Such a sequence is shorthand for the following commutative diagram:

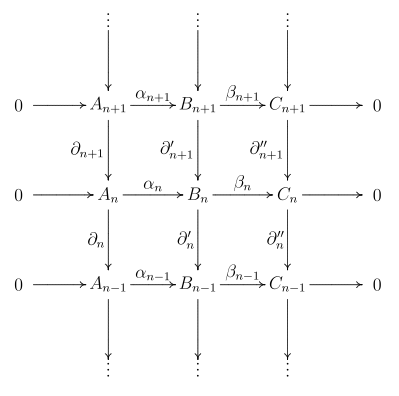
where the rows are exact sequences and each column is a chain complex.

The zig-zag lemma asserts that there is a collection of boundary maps

${\displaystyle \delta _{n}:H_{n}({\mathcal {C}})\longrightarrow H_{n-1}({\mathcal {A}}),}$

that makes the following sequence exact:

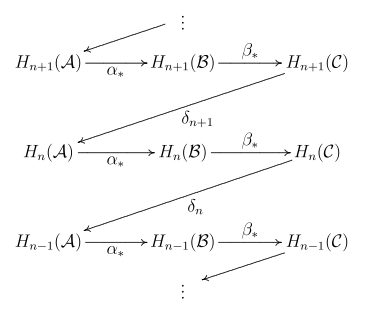
The maps ${\displaystyle \alpha _{*}^{}}$ and ${\displaystyle \beta _{*}^{}}$ are the usual maps induced by homology. The boundary maps ${\displaystyle \delta _{n}^{}}$ are explained below. The name of the lemma arises from the "zig-zag" behavior of the maps in the sequence. A variant version of the zig-zag lemma is commonly known as the "snake lemma" (it extracts the essence of the proof of the zig-zag lemma given below).

Construction of the boundary maps

The maps ${\displaystyle \delta _{n}^{}}$ are defined using a standard diagram chasing argument. Let ${\displaystyle c\in C_{n}}$ represent a class in ${\displaystyle H_{n}({\mathcal {C}})}$, so ${\displaystyle \partial _{n}''(c)=0}$. Exactness of the row implies that ${\displaystyle \beta _{n}^{}}$ is surjective, so there must be some ${\displaystyle b\in B_{n}}$ with ${\displaystyle \beta _{n}^{}(b)=c}$. By commutativity of the diagram,

${\displaystyle \beta _{n-1}\partial _{n}'(b)=\partial _{n}''\beta _{n}(b)=\partial _{n}''(c)=0.}$

By exactness,

${\displaystyle \partial _{n}'(b)\in \ker \beta _{n-1}=\mathrm {im} \alpha _{n-1}.}$

Thus, since ${\displaystyle \alpha _{n-1}^{}}$ is injective, there is a unique element ${\displaystyle a\in A_{n-1}}$ such that ${\displaystyle \alpha _{n-1}(a)=\partial _{n}'(b)}$. This is a cycle, since ${\displaystyle \alpha _{n-2}^{}}$ is injective and

${\displaystyle \alpha _{n-2}\partial _{n-1}(a)=\partial _{n-1}'\alpha _{n-1}(a)=\partial _{n-1}'\partial _{n}'(b)=0,}$

since ${\displaystyle \partial ^{2}=0}$. That is, ${\displaystyle \partial _{n-1}(a)\in \ker \alpha _{n-2}=\{0\}}$. This means ${\displaystyle a}$ is a cycle, so it represents a class in ${\displaystyle H_{n-1}({\mathcal {A}})}$. We can now define

${\displaystyle \delta _{}^{}[c]=[a].}$

With the boundary maps defined, one can show that they are well-defined (that is, independent of the choices of c and b). The proof uses diagram chasing arguments similar to that above. Such arguments are also used to show that the sequence in homology is exact at each group.

See also

• Mayer–Vietoris sequence

References

• Hatcher, Allen (2002). Algebraic Topology. Cambridge University Press. ISBN 0-521-79540-0.
• Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556
• Munkres, James R. (1993). Elements of Algebraic Topology. New York: Westview Press. ISBN 0-201-62728-0.