Z-channel (information theory)

In coding theory and information theory, a Z-channel (binary asymmetric channel) is a communications channel used to model the behaviour of some data storage systems.

The Z-channel sees each 0 bit of a message transmitted correctly always and each 1 bit transmitted correctly with probability 1–p, due to noise across the transmission medium.

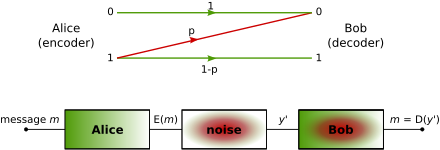
Definition

A Z-channel is a channel with binary input and binary output, where each 0 bit is transmitted correctly, but each 1 bit has probability p of being transmitted incorrectly as a 0, and probability 1–p of being transmitted correctly as a 1. In other words, if X and Y are the random variables describing the probability distributions of the input and the output of the channel, respectively, then the crossovers of the channel are characterized by the conditional probabilities:[1]

${\displaystyle {\begin{aligned}\operatorname {Pr} [Y=0|X=0]&=1\\\operatorname {Pr} [Y=0|X=1]&=p\\\operatorname {Pr} [Y=1|X=0]&=0\\\operatorname {Pr} [Y=1|X=1]&=1-p\end{aligned}}}$

Capacity

The channel capacity ${\displaystyle {\mathsf {cap}}(\mathbb {Z} )}$ of the Z-channel ${\displaystyle \mathbb {Z} }$ with the crossover 1 → 0 probability p, when the input random variable X is distributed according to the Bernoulli distribution with probability ${\displaystyle \alpha }$ for the occurrence of 0, is given by the following equation:

${\displaystyle {\mathsf {cap}}(\mathbb {Z} )={\mathsf {H}}\left({\frac {1}{1+2^{{\mathsf {s}}(p)}}}\right)-{\frac {{\mathsf {s}}(p)}{1+2^{{\mathsf {s}}(p)}}}=\log _{2}(1{+}2^{-{\mathsf {s}}(p)})=\log _{2}\left(1+(1-p)p^{p/(1-p)}\right)}$

where ${\displaystyle {\mathsf {s}}(p)={\frac {{\mathsf {H}}(p)}{1-p}}}$ for the binary entropy function ${\displaystyle {\mathsf {H}}(\cdot )}$.

This capacity is obtained when the input variable X has Bernoulli distribution with probability ${\displaystyle \alpha }$ of having value 1 and ${\displaystyle 1-\alpha }$ of value 0, where:

${\displaystyle \alpha ={\frac {1}{(1-p)(1+2^{{\mathsf {H}}(p)/(1-p)})}},}$

For small p, the capacity is approximated by

${\displaystyle {\mathsf {cap}}(\mathbb {Z} )\approx 1-0.5{\mathsf {H}}(p)}$

as compared to the capacity ${\displaystyle 1{-}{\mathsf {H}}(p)}$ of the binary symmetric channel with crossover probability p.

Calculation[2]

${\displaystyle {\mathsf {cap}}(\mathbb {Z} )=\max _{\alpha }\{{\mathsf {H}}(Y)-{\mathsf {H}}(Y\mid X)\}=\max _{\alpha }{\Bigl \{}{\mathsf {H}}(Y)-\sum _{x\in \{0,1\}}{\mathsf {H}}(Y\mid X=x){\mathsf {Prob}}\{X=x\}{\Bigr \}}}$ ${\displaystyle =\max _{\alpha }\{{\mathsf {H}}((1-\alpha )(1-p))-{\mathsf {H}}(Y\mid X=1){\mathsf {Prob}}\{X=1\}\}}$ ${\displaystyle =\max _{\alpha }\{{\mathsf {H}}((1-\alpha )(1-p))-(1-\alpha ){\mathsf {H}}(p)\},}$ To find the maximum we differentiate ${\displaystyle {\frac {d}{d\alpha }}{\mathsf {cap}}(\mathbb {Z} )=-(1-p)\log _{2}\left({\frac {1-(1-\alpha )(1-p)}{(1-\alpha )(1-p)}}\right)+{\mathsf {H}}(p)}$ And we see the maximum is attained for ${\displaystyle \alpha =1-{\frac {1}{(1-p)(1+2^{{\mathsf {H}}(p)/(1-p)})}},}$ yielding the following value of ${\displaystyle {\mathsf {cap}}(\mathbb {Z} )}$ as a function of p ${\displaystyle {\mathsf {cap}}(\mathbb {Z} )={\mathsf {H}}\left({\frac {1}{1+2^{{\mathsf {s}}(p)}}}\right)-{\frac {{\mathsf {s}}(p)}{1+2^{{\mathsf {s}}(p)}}}=\log _{2}(1{+}2^{-{\mathsf {s}}(p)})=\log _{2}\left(1+(1-p)p^{p/(1-p)}\right)\;{\textrm {where}}\;{\mathsf {s}}(p)={\frac {{\mathsf {H}}(p)}{1-p}}.}$

For any p, ${\displaystyle \alpha <0.5}$ (i.e. more 0s should be transmitted than 1s) because transmitting a 1 introduces noise. As ${\displaystyle p\rightarrow 1}$, the limiting value of ${\displaystyle \alpha }$ is ${\displaystyle {\frac {1}{e}}}$.[2]

Bounds on the size of an asymmetric-error-correcting code

Define the following distance function ${\displaystyle {\mathsf {d}}_{A}(\mathbf {x} ,\mathbf {y} )}$ on the words ${\displaystyle \mathbf {x} ,\mathbf {y} \in \{0,1\}^{n}}$ of length n transmitted via a Z-channel

${\displaystyle {\mathsf {d}}_{A}(\mathbf {x} ,\mathbf {y} ){\stackrel {\vartriangle }{=}}\max \left\{{\big |}\{i\mid x_{i}=0,y_{i}=1\}{\big |},{\big |}\{i\mid x_{i}=1,y_{i}=0\}{\big |}\right\}.}$

Define the sphere ${\displaystyle V_{t}(\mathbf {x} )}$ of radius t around a word ${\displaystyle \mathbf {x} \in \{0,1\}^{n}}$ of length n as the set of all the words at distance t or less from ${\displaystyle \mathbf {x} }$, in other words,

${\displaystyle V_{t}(\mathbf {x} )=\{\mathbf {y} \in \{0,1\}^{n}\mid {\mathsf {d}}_{A}(\mathbf {x} ,\mathbf {y} )\leq t\}.}$

A code ${\displaystyle {\mathcal {C}}}$ of length n is said to be t-asymmetric-error-correcting if for any two codewords ${\displaystyle \mathbf {c} \neq \mathbf {c} '\in \{0,1\}^{n}}$, one has ${\displaystyle V_{t}(\mathbf {c} )\cap V_{t}(\mathbf {c} ')=\emptyset }$. Denote by ${\displaystyle M(n,t)}$ the maximum number of codewords in a t-asymmetric-error-correcting code of length n.

The Varshamov bound. For n≥1 and t≥1,

${\displaystyle M(n,t)\leq {\frac {2^{n+1}}{\sum _{j=0}^{t}{\left({\binom {\lfloor n/2\rfloor }{j}}+{\binom {\lceil n/2\rceil }{j}}\right)}}}.}$

The constant-weight code bound. For n > 2t ≥ 2, let the sequence B₀, B₁, ..., B_n-2t-1 be defined as

${\displaystyle B_{0}=2,\quad B_{i}=\min _{0\leq j<i}\{B_{j}+A(n{+}t{+}i{-}j{-}1,2t{+}2,t{+}i)\}}$ for ${\displaystyle i>0}$.

Then ${\displaystyle M(n,t)\leq B_{n-2t-1}.}$

Notes

1. MacKay (2003), p. 148.
2. MacKay (2003), p. 159.

References

• MacKay, David J.C. (2003). Information Theory, Inference, and Learning Algorithms. Cambridge University Press. ISBN 0-521-64298-1.
• Kløve, T. (1981). "Error correcting codes for the asymmetric channel". Technical Report 18–09–07–81. Norway: Department of Informatics, University of Bergen.
• Verdú, S. (1997). "Channel Capacity (73.5)". The electrical engineering handbook (second ed.). IEEE Press and CRC Press. pp. 1671–1678.
• Tallini, L.G.; Al-Bassam, S.; Bose, B. (2002). On the capacity and codes for the Z-channel. Proceedings of the IEEE International Symposium on Information Theory. Lausanne, Switzerland. p. 422.