Young's inequality for products

In mathematics, Young's inequality for products is a mathematical inequality about the product of two numbers.[1] The inequality is named after William Henry Young and should not be confused with Young's convolution inequality.

Young's inequality for products can be used to prove Hölder's inequality. It is also widely used to estimate the norm of nonlinear terms in PDE theory, since it allows one to estimate a product of two terms by a sum of the same terms raised to a power and scaled.

Standard version for conjugate Hölder exponents

The standard form of the inequality is the following:

Theorem — If a and b are nonnegative real numbers and p and q are real numbers greater than 1 such that 1/p + 1/q = 1, then

${\displaystyle ab\leq {\frac {a^{p}}{p}}+{\frac {b^{q}}{q}}~.}$

The equality holds if and only if a^p = b^q.

This form of Young's inequality can be proved by Jensen's inequality and can be used to prove Hölder's inequality.

Proof —

The claim is certainly true if a = 0 or b = 0. Therefore, assume a > 0 and b > 0 in the following. Put t = 1/p, and (1 − t) = 1/q. Then since the logarithm function is concave,

${\displaystyle \ln(ta^{p}+(1-t)b^{q})\geq t\ln(a^{p})+(1-t)\ln(b^{q})=\ln(a)+\ln(b)=\ln(ab)}$

with the equality holding if and only if a^p = b^q. Young's inequality follows by exponentiating.

Young's inequality may equivalently be written as

${\displaystyle a^{\alpha }b^{\beta }\leq \alpha a+\beta b,\qquad \,0\leq \alpha ,\beta \leq 1,\quad \ \alpha +\beta =1~.}$

Where this is just the concavity of the logarithm function. Equality holds if and only if a = b or ${\displaystyle \{\alpha ,\beta \}=\{0,1\}}$.

Generalizations

Theorem[2] — Suppose a > 0 and b > 0. If 1 < p < ∞ and q := p/p - 1 then

ab = min0 < t < ∞ t ^p a ^p/p + t ^{- q} b ^q/q.

Note that by letting t = 1 and replacing a (resp. b) with a^1/p (resp. b^1/q), we obtain

a^1/p b^1/q ≤ a/p + b/q

which is useful for proving Hölder's inequality.

Proof[2] —

Define a real-valued function f on the positive real numbers by

f (t) := t ^p a ^p/p + t ^-q b ^q/q

for every t > 0 and then calculate its minimum.

Theorem — :${\displaystyle \prod _{i}{a_{i}}^{\alpha _{i}}\leq \sum _{i}\alpha _{i}a_{i},\quad 0\leq \alpha _{i}\leq 1,\quad \ \sum _{i}\alpha _{i}=1~.}$ The equality holds if and only if all the ${\displaystyle a_{i}}$s with non-zero ${\displaystyle \alpha _{i}}$s are equal.

Elementary case

An elementary case of Young's inequality is the inequality with exponent 2,

${\displaystyle ab\leq {\frac {a^{2}}{2}}+{\frac {b^{2}}{2}},}$

which also gives rise to the so-called Young's inequality with ε (valid for every ε > 0), sometimes called the Peter–Paul inequality. [3] This name refers to the fact that tighter control of the second term is achieved at the cost of losing some control of the first term – one must "rob Peter to pay Paul"

${\displaystyle ab\leq {\frac {a^{2}}{2\varepsilon }}+{\frac {\varepsilon b^{2}}{2}}.}$

Proof

Young's inequality with exponent 2 is the special case p = q = 2. However, it has a more elementary proof.

Start by observing that the square of every real number is zero or positive. Therefore, for every pair of real numbers a and b we can write:

${\displaystyle 0\leq (a-b)^{2}}$

Work out the square of the right hand side:

${\displaystyle 0\leq a^{2}-2ab+b^{2}}$

Add '2ab' to both sides:

${\displaystyle 2ab\leq a^{2}+b^{2}}$

Divide both sides by 2 and we have Young's inequality with exponent 2:

${\displaystyle ab\leq {\frac {a^{2}}{2}}+{\frac {b^{2}}{2}}}$

Young's inequality with ε follows by substituting ${\displaystyle a'}$ and ${\displaystyle b'}$ as below into Young's inequality with exponent 2:

${\displaystyle a'=a/{\sqrt {\varepsilon }},{\text{ }}b'={\sqrt {\varepsilon }}b.}$

Matricial generalization

T. Ando proved a generalization of Young's inequality for complex matrices ordered by Loewner ordering.[4] It states that for any pair A, B of complex matrices of order n there exists a unitary matrix U such that

${\displaystyle U^{*}|AB^{*}|U\preceq {\frac {1}{p}}|A|^{p}+{\frac {1}{q}}|B|^{q},}$

where * denotes the conjugate transpose of the matrix and ${\displaystyle |A|={\sqrt {A^{*}A}}}$.

Standard version for increasing functions

The area of the rectangle a,b can't be larger than sum of the areas under the functions ${\displaystyle f}$ (red) and ${\displaystyle f^{-1}}$ (yellow)

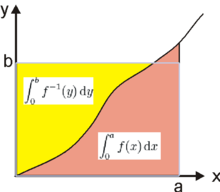
For the standard version[5][6] of the inequality, let f denote a real-valued, continuous and strictly increasing function on [0, c] with c > 0 and f(0) = 0. Let f⁻¹ denote the inverse function of f. Then, for all a ∈ [0, c] and b ∈ [0, f(c)],

${\displaystyle ab\leq \int _{0}^{a}f(x)\,dx+\int _{0}^{b}f^{-1}(x)\,dx}$

with equality if and only if b = f(a).

With ${\displaystyle f(x)=x^{p-1}}$ and ${\displaystyle f^{-1}(y)=y^{q-1}}$, this reduces to standard version for conjugate Hölder exponents.

For details and generalizations we refer to the paper of Mitroi & Niculescu [7].

Generalization using Fenchel–Legendre transforms

If f is a convex function and its Legendre transformation (convex conjugate) is denoted by g, then

${\displaystyle ab\leq f(a)+g(b).}$

This follows immediately from the definition of the Legendre transform.

More generally, if f is a convex function defined on a real vector space ${\displaystyle X}$ and its convex conjugate is denoted by ${\displaystyle f^{\star }}$ (and is defined on the dual space ${\displaystyle X^{\star }}$), then

${\displaystyle \langle u,v\rangle \leq f^{\star }(u)+f(v).}$

where ${\displaystyle \langle \cdot ,\cdot \rangle :X^{\star }\times X\to \mathbb {R} }$ is the dual pairing.

Examples

• The Legendre transform of f(a) = a^p/p is g(b) = b^q/q with q such that 1/p + 1/q = 1, and thus Young's inequality for conjugate Hölder exponents mentioned above is a special case.
• The Legendre transform of f(a) = e^a – 1 is g(b) = 1 − b + b ln b, hence ab ≤ e^a − b + b ln b for all non-negative a and b. This estimate is useful in large deviations theory under exponential moment conditions, because b ln b appears in the definition of relative entropy, which is the rate function in Sanov's theorem.

See also

• Convex conjugate
• Integral of inverse functions
• Legendre transformation

Notes

1. Young, W. H. (1912), "On classes of summable functions and their Fourier series", Proceedings of the Royal Society A, 87 (594): 225–229, doi:10.1098/rspa.1912.0076, JFM 43.1114.12, JSTOR 93236
2. Jarchow 1981, pp. 47-55. sfn error: no target: CITEREFJarchow1981 (help)
3. Tisdell, Chris (2013), The Peter Paul Inequality, YouTube video on Dr Chris Tisdell's YouTube channel,
4. T. Ando (1995). "Matrix Young Inequalities". In Huijsmans, C. B.; Kaashoek, M. A.; Luxemburg, W. A. J.; et al. (eds.). Operator Theory in Function Spaces and Banach Lattices. Springer. pp. 33–38. ISBN 978-3-0348-9076-2.
5. Hardy, G. H.; Littlewood, J. E.; Pólya, G. (1952) [1934], Inequalities, Cambridge Mathematical Library (2nd ed.), Cambridge: Cambridge University Press, ISBN 0-521-05206-8, MR 0046395, Zbl 0047.05302, Chapter 4.8
6. Henstock, Ralph (1988), Lectures on the Theory of Integration, Series in Real Analysis Volume I, Singapore, New Jersey: World Scientific, ISBN 9971-5-0450-2, MR 0963249, Zbl 0668.28001, Theorem 2.9
7. Mitroi, F. C., & Niculescu, C. P. (2011). An extension of Young's inequality. In Abstract and Applied Analysis (Vol. 2011). Hindawi.

References

• Jarchow, Hans (1981). Locally convex spaces. Stuttgart: B.G. Teubner. ISBN 978-3-519-02224-4. OCLC 8210342.CS1 maint: ref=harv (link)

External links

• Young's Inequality at PlanetMath
• Weisstein, Eric W. "Young's Inequality". MathWorld.