Whitney's planarity criterion

In mathematics, Whitney's planarity criterion is a matroid-theoretic characterization of planar graphs, named after Hassler Whitney.[1] It states that a graph G is planar if and only if its graphic matroid is also cographic (that is, it is the dual matroid of another graphic matroid).

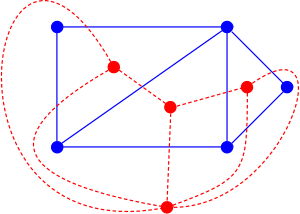
A planar graph and its dual. Every cycle in the blue graph is a minimal cut in the red graph, and vice versa, so the two graphs are algebraic duals and have dual graphic matroids.

In purely graph-theoretic terms, this criterion can be stated as follows: There must be another (dual) graph G'=(V',E') and a bijective correspondence between the edges E' and the edges E of the original graph G, such that a subset T of E forms a spanning tree of G if and only if the edges corresponding to the complementary subset E-T form a spanning tree of G'.

Algebraic duals

An equivalent form of Whitney's criterion is that a graph G is planar if and only if it has a dual graph whose graphic matroid is dual to the graphic matroid of G. A graph whose graphic matroid is dual to the graphic matroid of G is known as an algebraic dual of G. Thus, Whitney's planarity criterion can be expressed succinctly as: a graph is planar if and only if it has an algebraic dual.

Topological duals

If a graph is embedded into a topological surface such as the plane, in such a way that every face of the embedding is a topological disk, then the dual graph of the embedding is defined as the graph (or in some cases multigraph) H that has a vertex for every face of the embedding, and an edge for every adjacency between a pair of faces. According to Whitney's criterion, the following conditions are equivalent:

  • The surface on which the embedding exists is topologically equivalent to the plane, sphere, or punctured plane
  • H is an algebraic dual of G
  • Every simple cycle in G corresponds to a minimal cut in H, and vice versa
  • Every simple cycle in H corresponds to a minimal cut in G, and vice versa
  • Every spanning tree in G corresponds to the complement of a spanning tree in H, and vice versa.[2]

It is possible to define dual graphs of graphs embedded on nonplanar surfaces such as the torus, but these duals do not generally have the correspondence between cuts, cycles, and spanning trees required by Whitney's criterion.

gollark: Shame PC speakers aren't around so you can't remotely beep them.
gollark: That makes you a BLASPH.
gollark: Ah. I see.
gollark: <@&198138780132179968> <@270035320894914560>/aus210 has stolen my (enchanted with Unbreaking something/Mending) elytra.I was in T79/i02p/n64c/pjals' base (aus210 wanted help with some code, and they live in the same place with some weird connecting tunnels) and came across an armor stand (it was in an area of the base I was trusted in - pjals sometimes wants to demo stuff to me or get me to help debug, and the claim organization is really odd). I accidentally gave it my neural connector, and while trying to figure out how to get it back swapped my armor onto it (turns out shiftrightclick does that). Eventually I got them both back, but while my elytra was on the stand aus210 stole it. I asked for it back and they repeatedly denied it.They have claimed:- they can keep it because I intentionally left it there (this is wrong, and I said so)- there was no evidence that it was mine so they can keep it (...)EDIT: valithor got involved and got them to actually give it back, which they did after ~10 minutes of generally delaying, apparently leaving it in storage, and dropping it wrong.
gollark: Someone had a problem with two mutually recursive functions (one was defined after the other), so I fixed that for them. Then I explained stack overflows and how that made their design (`mainScreen` calls `itemScreen` calls `mainScreen`...) problematic. Their suggested solution was to just capture the error and restart the program. Since they weren't entirely sure how to do *that*, their idea was to make it constantly ping their webserver and have another computer reboot it if it stopped.

References
  1. Whitney, Hassler (1932), "Non-separable and planar graphs", Transactions of the American Mathematical Society, 34 (2): 339–362, doi:10.1090/S0002-9947-1932-1501641-2.
  2. Tutte, W. T. (1965), "Lectures on matroids", Journal of Research of the National Bureau of Standards, 69B: 1–47, doi:10.6028/jres.069b.001, MR 0179781. See in particular section 2.5, "Bon-matroid of a graph", pp. 5–6, section 5.6, "Graphic and co-graphic matroids", pp. 19–20, and section 9, "Graphic matroids", pp. 38–47.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.