Volterra's function
In mathematics, Volterra's function, named for Vito Volterra, is a real-valued function V defined on the real line R with the following curious combination of properties:
- V is differentiable everywhere
- The derivative V ′ is bounded everywhere
- The derivative is not Riemann-integrable.
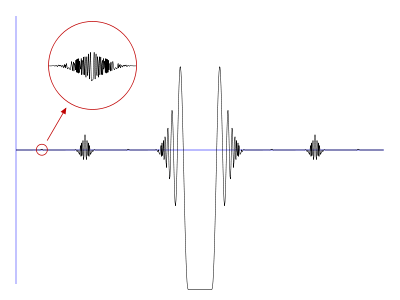
Definition and construction
The function is defined by making use of the Smith–Volterra–Cantor set and "copies" of the function defined by for and . The construction of V begins by determining the largest value of x in the interval [0, 1/8] for which f ′(x) = 0. Once this value (say x0) is determined, extend the function to the right with a constant value of f(x0) up to and including the point 1/8. Once this is done, a mirror image of the function can be created starting at the point 1/4 and extending downward towards 0. This function will be defined to be 0 outside of the interval [0, 1/4]. We then translate this function to the interval [3/8, 5/8] so that the resulting function, which we call f1, is nonzero only on the middle interval of the complement of the Smith–Volterra–Cantor set. To construct f2, f ′ is then considered on the smaller interval [0,1/32], truncated at the last place the derivative is zero, extended, and mirrored the same way as before, and two translated copies of the resulting function are added to f1 to produce the function f2. Volterra's function then results by repeating this procedure for every interval removed in the construction of the Smith–Volterra–Cantor set; in other words, the function V is the limit of the sequence of functions f1, f2, ...
Further properties
Volterra's function is differentiable everywhere just as f (as defined above) is. One can show that f ′(x) = 2x sin(1/x) - cos(1/x) for x ≠ 0, which means that in any neighborhood of zero, there are points where f ′ takes values 1 and −1. Thus there are points where V ′ takes values 1 and −1 in every neighborhood of each of the endpoints of intervals removed in the construction of the Smith–Volterra–Cantor set S. In fact, V ′ is discontinuous at every point of S, even though V itself is differentiable at every point of S, with derivative 0. However, V ′ is continuous on each interval removed in the construction of S, so the set of discontinuities of V ′ is equal to S.
Since the Smith–Volterra–Cantor set S has positive Lebesgue measure, this means that V ′ is discontinuous on a set of positive measure. By Lebesgue's criterion for Riemann integrability, V ′ is not Riemann integrable. If one were to repeat the construction of Volterra's function with the ordinary measure-0 Cantor set C in place of the "fat" (positive-measure) Cantor set S, one would obtain a function with many similar properties, but the derivative would then be discontinuous on the measure-0 set C instead of the positive-measure set S, and so the resulting function would have a Riemann integrable derivative.