Virtual displacement

In analytical mechanics, a branch of applied mathematics and physics, a virtual displacement δr_i "is an assumed infinitesimal change of system coordinates occurring while time is held constant. It is called virtual rather than real since no actual displacement can take place without the passage of time."[1]^:263 This way, virtual displacements are spatial displacements exclusively – time is fixed while they occur. When computing virtual differentials of quantities that are functions of space and time coordinates, no dependence on time is considered (formally equivalent to saying δt = 0).

For the particle trajectory ${\displaystyle x(t)}$ and its virtual trajectory ${\displaystyle x'(t)}$, at position ${\displaystyle x_{1}}$, time ${\displaystyle t_{1}}$, the virtual displacement is ${\displaystyle \delta x}$ 。 The starting and ending positions for both trajectories are at ${\displaystyle x_{0}}$ and ${\displaystyle x_{2}}$ respectively.

One degree of freedom.

Two degrees of freedom.

Constraint force C and virtual displacement δr for a particle of mass m confined to a curve. The resultant non-constraint force is N. The components of virtual displacement are related by a constraint equation.

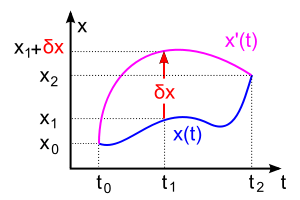
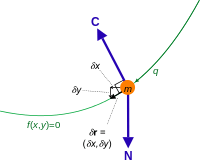
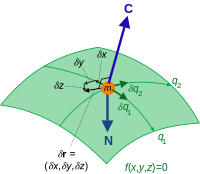
In modern terminology virtual displacement is a tangent vector to the manifold representing the constraints at a fixed time. Unlike regular displacement which arises from differentiating with respect to time parameter t along the path of the motion (thus pointing in the direction of the motion), virtual displacement arises from differentiating with respect to the parameter ε enumerating paths of the motion varied in a manner consistent with the constraints (thus pointing at a fixed time in the direction tangent to the constraining manifold). The symbol δ is traditionally used to denote the corresponding derivative

${\displaystyle \delta =\left.{\frac {\partial }{\partial \epsilon }}\right|_{\epsilon =0}\,.}$

Comparison between virtual and actual displacements

Here we consider the total differential of any set of system position vectors, r_i, that are functions of other variables

${\displaystyle \lbrace q_{1},q_{2},...,q_{m}\rbrace }$

and time t. These position vectors are "on-shell" meaning they satisfy the Euler-Lagrange equations and solve for the true evolution trajectories of the system. In other words, these vectors move according to the constraint forces and actual forces of the system at every instant in time. The actual displacement is the differential of the on-shell solution:

${\displaystyle d\mathbf {r} _{i}={\frac {\partial \mathbf {r} _{i}}{\partial t}}dt+\sum _{j=1}^{m}{\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}dq_{j}}$

Now, imagine if we have an arbitrary path through the configuration space/manifold. This means it has to satisfy the constraints of the system but not the actual applied forces. We can think of that as the off-shell differential:

${\displaystyle \delta \mathbf {r} _{i}=\sum _{j=1}^{m}{\frac {\partial \mathbf {r} _{i}}{\partial q_{j}}}\delta q_{j}}$

This equation is used in Lagrangian mechanics to relate generalized coordinates, q_j, to virtual work, δW, and generalized forces, Q_j.

In the two degree-of-freedom example on the right, the actual displacement is the true trajectory of the particle moving on the two-dimensional surface. The virtual displacement is any tangent vector to the surface.

Virtual work

In analytical mechanics the concept of a virtual displacement, related to the concept of virtual work, is meaningful only when discussing a physical system subject to constraints on its motion. A special case of an infinitesimal displacement (usually notated dr), a virtual displacement (denoted δr) refers to an infinitesimal change in the position coordinates of a system such that the constraints remain satisfied [2].

For example, if a bead is constrained to move on a hoop, its position may be represented by the position coordinate θ, which gives the angle at which the bead is situated. Say that the bead is at the top. Moving the bead straight upwards from its height z to a height z + dz would represent one possible infinitesimal displacement, but would violate the constraint. The only possible virtual displacement would be a displacement from the bead's position, θ to a new position θ + δθ (where δθ could be positive or negative).

See also

• D'Alembert principle
• Virtual work

References

1. Torby, Bruce (1984). "Energy Methods". Advanced Dynamics for Engineers. HRW Series in Mechanical Engineering. United States of America: CBS College Publishing. ISBN 0-03-063366-4.
2. Goldstein, H.; Poole, C. P.; Safko, J. L. (2001). Classical Mechanics (3rd ed.). Addison-Wesley. p. 16. ISBN 978-0-201-65702-9.