Tunnel of Eupalinos

The Tunnel of Eupalinos or Eupalinian aqueduct (Greek: Ευπαλίνιον όρυγμα, romanized: Efpalinion orygma) is a tunnel of 1,036 m (3,399 ft) length running through Mount Kastro in Samos, Greece, built in the 6th century BC to serve as an aqueduct.[1] The tunnel is the second known tunnel in history which was excavated from both ends (Ancient Greek: ἀμφίστομον, romanized: amphistomon, "having two openings"), and the first with a geometry-based approach in doing so.[2] Today it is a popular tourist attraction.

Tunnel of Eupalinos
Inside one of the most spacious parts of the Eupalinian aqueduct.
Overview
LocationSamos Island, Greece
Coordinates37°41′38″N 26°55′48″E
StatusOpen
Operation
Openedcirca 6th century BCE
Technical
Design engineerEupalinos
Length1036 m

Early history
Inside the aqueduct

The Eupalinian aqueduct is described by Herodotus (Histories 3.60), without whom it might not have been discovered:

I have dwelt longer upon the history of the Samians than I should otherwise have done, because they are responsible for three of the greatest building and engineering feats in the Greek world: the first is a tunnel nearly a mile long, eight feet wide and eight feet high, driven clean through the base of a hill nine hundred feet in height. The whole length of it carries a second cutting thirty feet deep and three broad, along which water from an abundant source is led through pipes into the town. This was the work of a Megarian named Eupalinus, son of Naustrophus.[3]

The tunnel might also be referred to in the Homeric Hymn to Apollo, which mentions "watered Samos."[4] The tunnel was dug in the mid-sixth century BC, by two groups working under the direction of the engineer Eupalinos from Megara, in order to supply the ancient capital of Samos (today called Pythagoreion) with fresh water. This was necessary for demographic reasons: the city of Samos had outgrown the capacity of the wells and cisterns within the city's limits, but main source of fresh water on the island was on the other side of Mount Kastro from the city. It was of the utmost defensive importance; because the aqueduct ran underground, it could not easily be found by an enemy, who might otherwise cut off the water supply. The date of construction is not entirely clear. Herodotus mentions the tunnel in the context of his account of the tyrant Polycrates who ruled c. 540-522 BC, but he does not explicitly say that Polycrates was responsible for its construction. Aideen Carty suggests that it should be connected with the regime that overthrew the Geomori in the early sixth century BC, which granted citizenship to a large number of Megarians, perhaps including Eupalinos.[5] The Eupalinian aqueduct was used as an aqueduct for 1100 years, before it began to silt up. In the seventh century AD, the south end was used as a defensive refuge.[6]

Description

Spring and reservoir

The tunnel took water from an inland spring, located about 52 metres (171 ft) above sea level near the modern village of Ayiades. It discharges about 400 m3 of water per day. This spring was covered over. Two rectangular openings, each measuring 28 by 26 centimetres (11 by 10 in), feed the water into a large reservoir with a roughly elliptical ground plan. Fifteen large stone pillars support a roof of massive stone slabs. The spring was thus completely concealed from enemies. The construction of this reservoir seems to have caused the outlet of the spring to subside by several metres. At some point before the nineteenth century, a church dedicated to St John was built over the top of this reservoir, further hiding the spring's location.[7]

North channel

From the spring, a buried channel winds along the hillside to the northern tunnel mouth. The channel is 890 metres (2,920 ft) long, although the distance from the spring to the tunnel mouth as the crow flies is only 370 metres (1,210 ft). The channel is 60–70 centimetres (24–28 in) wide and about 5 metres (16 ft) deep. After it had been cut out of the bedrock, it was covered over with stone slabs and then buried. There are inspection shafts at regular intervals along the channel's course. The last 150 metres (490 ft) of this channel pass under a small hill. Vertical shafts were dug from the surface at intervals of 30–50 metres (98–164 ft) and then linked up to create a short tunnel, which brings the water .[8]

Tunnel of Eupalinos
Reinforced section of the tunnel, with pointed roof and polygonal masonry walls.

The tunnel through Mount Kastro carried the water for a distance of 1,036 metres (3,399 ft). The tunnel is generally 1.8 by 1.8 metres (5.9 by 5.9 ft). The southern half of the tunnel was dug to larger dimensions than the northern half, which in places is just wide enough for one person to squeeze through. The southern half, by contrast, benefits from being dug through a more stable rock stratum.[9] In three sections, a pointed roof of stone slabs was installed to prevent rockfalls. Two of these sections, covering 153 metres (502 ft), are near the north end of the tunnel; the third section is 12 metres (39 ft) m at the southern end of the tunnel. The walls of the tunnel were also faced with masonry in these sections, using polygonal masonry at the south end and large slabs at the northern end. In the Roman Imperial period, barrel vaults were built with small stones and plaster to reinforce other sections of the tunnel.[10]

The width of the tunnel means that there would have been space for only two diggers to work at a time. To speed up the process, the tunnel was dug from both ends simultaneously. H. J. Kienast calculates that such workers would have been able to dig out 12–15 centimetres (4.7–5.9 in) of stone per day, meaning that the entire tunnel took at least eight years to dig.[9]

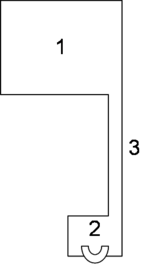
Cross-section of the tunnel (1), with the water channel containing the actual water-pipe (2), and a vertical shaft linking the two (3).

The floor of the tunnel is nearly horizontal and roughly 3 metres (9.8 ft) above the level of the water at its source. Apparently, the subsidence at the spring lowered the level of the water after work had begun, leaving the tunnel too high. A separate channel had to be dug below the east half of the tunnel to carry the water itself. It increases in depth over the course of the tunnel, from 4 metres (13 ft) m deep at the north end to 8.5 metres (28 ft) at the southern end. Vertical shafts link this channel to the main tunnel roughly every ten metres. These were dug from the tunnel and then linked together to create the channel; once construction was finished, they served as inspection shafts. Debris from this channel was simply dumped in the main tunnel.[11]

A number of symbols and letters painted on the wall testify to a wide range of measurements. Three of them (Κ, Ε, and ΚΒ on the east wall), clearly mark the points where vertical shafts were cut. On the west wall, there are letters in alphabetical order at a regular interval of 20.59 metres (67.6 ft), which indicate that this was the basic unit of measurement used by Eupalinos (it is one fiftieth of the planned course through the mountain). The meanings of the other symbols have not yet been determined.[12]

Within the channel, the water was transported in a pipe made from terracotta sections, which were 72 centimetres (28 in) long and 26 centimetres (10 in) in diameter. The full pipe must have required around 5,000 of these sections. They were joined to one another with lime mortar. The top quarter of the pipes was cut open to allow sediment and other detritus to be removed, so that the aqueduct did not silt up. A break in the pipe near the north entrance of tunnel led to large amounts of mud entering the pipe, which had to be cleared out regularly.[13]

In the seventh century AD, when the aqueduct had ceased to operate, the southern section of the tunnel was converted to serve as refuge. This included the construction of a cistern 400 metres (1,300 ft) from the southern entrance to collect water dripping from a vein in the rock.[14]

Southern channel

Shortly before the southern mouth of the tunnel, the water channel diverges from the main tunnel and heads through the rock in a hidden channel like that to the north of the tunnel, which is buried just below the surface of the ground. It carries the water eastwards to the town of Pythagoreion. Only about 500 metres (1,600 ft) of this channel have been excavated, but its total length must have been around 1,000 metres (3,300 ft). Two monumental fountains on the hillside inside the city seem to be on the line of this channel. They contained a reservoir and basins from which people could collect the water and carry it to their homes.[15]

Surveying techniques & construction

In order to align the two tunnels, Eupalinos first constructed a "mountain line", running over the top of the mountain at the easiest part of the summit even though this gave a non-optimal position both for feeding water into the tunnel and for water delivery to the city. He connected a “south line” to the mountain line at the south side going straight into the mountain, which formed the south tunnel. At the north side a “north line” is connected to the mountain line, guiding the cut into the mountain from the north side.[16] As the workers dug, they checked that their course remained straight by making sightings back towards the entrance of the tunnel. This is shown by a point in the southern half of the tunnel where the course accidentally diverged to the west and had to be corrected; a notch has been cut out of the rock on the inside of the curve, in order to restore the sight line.[17]

After 273 metres (896 ft) from the northern end, an area full of water, weak rock and mud forced Eupalinos to modify his plan and direct the tunnel to the west. When leaving the line Eupalinos planned his diversion as an isosceles triangle, with angles 22.5, 45, and 22.5 degrees. Measuring errors occurred and Eupalinos slightly overshot. When this was realised, the north tunnel was redirected to the east once more. The cutting of the south tunnel was completely straight, but stopped after 390 metres (1,280 ft).[16][18]

Eupalinos used a unit of 20.59 metres (67.6 ft) metres for distance measurements and a unit of 7.5 degrees (1/12 of a right angle) for setting out directions.[16][19]

Meeting point

The north and south halves of the tunnel meet in the middle of the mountain at a dog-leg, a technique to assure they did not miss each other (This method is documented by Hermann J. Kienast and other researchers). In planning the dig, Eupalinos used now well-known principles of geometry, codified by Euclid several centuries later. With a length of 1,036 metres (3,399 ft), the Eupalinian subterranean aqueduct is famous today as one of the masterpieces of ancient engineering. When the two tunnels reach within earshot, which can be estimated for this type of rock to approximate 12 metres (39 ft), the tunnels could be directed towards each other, but a high level of accuracy was required to reach that point. Errors in measurement and staking could cause Eupalinos to miss the meeting point of the two teams, either horizontally or vertically. He therefore employed the following techniques.

In the horizontal plane

Eupalinos calculated the expected position of the meeting point in the mountain. Since two parallel lines never meet, an error of more than two metres (6.6 ft) horizontally meant that the north and south tunnels would never meet. Therefore, Eupalinos changed the direction of both tunnels, as shown in the picture (the north tunnel to the left and the south tunnel to the right). This gave a 17 metres (56 ft) wider catching width, so that a crossing point would be guaranteed, even if the tunnels were previously parallel and far away. They thus meet at nearly a right angle.[20]

In the vertical plane

At the start of work, Eupalinos levelled around the mountain probably following a contour line in order to ensure that both tunnels were started at the same altitude. The possibility of vertical deviations in the process of excavation remained, however. He increased the possibility of the two tunnels meeting each other, by increasing the height of both tunnels at the point near the join. In the north tunnel he kept the floor horizontal and increased the height of the roof by 2.5 metres (8.2 ft), while in the south tunnel he kept the roof horizontal and lowered the level of the floor by 0.6 metres (2.0 ft). His precautions as to vertical deviation proved unnecessary, however, since measurements show that there was very little error. At the rendezvous, the closing error in altitude for the two tunnels was a few millimetres.[16][21]

Rediscovery and excavation
The sign at the end of the part of the Eupalinian aqueduct that is open to the public.

Scholars began searching for the tunnel in the 19th century, inspired by the reference to it in Herodotus. The French archaeologist, Victor Guérin identified the spring that feeds the aqueduct in 1853 and the beginnings of the channel. In 1882, work began on clearing the tunnel with the goal of bringing it back into use. This proved too difficult and the effort was called off, but it allowed Ernst Fabricius to investigate the tunnel on behalf of the German Archaeological Institute. He published the results in 1884 as "Die Wasserleitung des Eupalinos."[22] Full excavations of the tunnel were carried out by Ulf Jantzen from 1971-1973, who finally cleared the full length of the tunnel, which had become filled with silt. A full survey of the tunnel with detailed geodetic measurements was carried out by Hermann J. Kienast.[23] Portions of the tunnel are open to the public.

gollark: Perhaps some combination of wool, skystone and sandstone could work nicely.
gollark: No.
gollark: I was thinking about red sandstone and skyblocks, but that sounds also horrible.
gollark: That sounds aesthetically horrible.
gollark: I'm trying to design a nice-looking AE2 controller room, any ideas?

References
  1. Andreas Nikolaos Angelakis; Larry W. Mays; Demetris Koutsoyiannis (2012). Evolution of Water Supply Through the Millennia. IWA Publishing. pp. 85–87, 264, 355, 407. ISBN 9781843395409.
  2. The oldest known tunnel at which two teams advanced simultaneously is the Siloam tunnel in Jerusalem, completed around 700 BC. It has been posited that it was dug by maintaining depths close enough to the surface of the solid karst that the diggers could hear loud banging from the surface guiding the two teams towards one another. Frumkin, Amos; Shimron, Aryeh (2006). "Tunnel engineering in the Iron Age: Geoarchaeology of the Siloam Tunnel, Jerusalem". Journal of Archaeological Science. 33 (2): 227–237. doi:10.1016/j.jas.2005.07.018.
  3. Herodotus (1954). The Histories. Translated by Aubrey de Sélincourt. Harmondsworth: Penguin. pp. 199–200.
  4. Homeric Hymn to Apollo, 41
  5. Carty, Aideen (2015). Polycrates, Tyrant of Samos: New Light on Archaic Greece. Stuttgart: Franz Steiner Verlag. p. 31. ISBN 9783515108980.
  6. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 16 & 35.
  7. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 17–20.
  8. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 20–22.
  9. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 22–24.
  10. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 28–31.
  11. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 24–27.
  12. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 47–51.
  13. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 31–35.
  14. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 35–36.
  15. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 17–18, 24–25.
  16. Olson, Åke (2012). "How Eupalinos navigated his way through the mountain: An empirical approach to the geometry of Eupalinos". Anatolia Antiqua. Institut Français d’Études Anatoliennes. XX: 25–34. doi:10.3406/anata.2012.1323.
  17. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 41–42.
  18. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 46 & 52–55.
  19. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 52–55.
  20. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 43–44, 52–55.
  21. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 40 & 56–57.
  22. Fabricius in Mitteilungen des Deutschen Archäologischen Instituts (Athen) 9 (1884) pp. 165–192.
  23. Kienast, H. J. (2005). The Aqueduct of Eupalinos on Samos. Athens. pp. 14–16.

Literature
  • Apostol, Tom M. (2004). "The Tunnel of Samos" (PDF). Engineering and Science. 1: 30–40.
  • Kienast, Hermann J. (2005). The Aqueduct of Eupalinos on Samos. Athens: Ministry of Culture Archaeological Receipts Fund. p. 60. ISBN 960-214-424-6.
  • Olson, Åke (2012). "How Eupalinos navigated his way through the mountain-An empirical approach to the geometry of Eupalinos". Anatolia Antiqua, Institut Français d'Études Anatoliennes. XX: 25–34.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.