Truncated triakis icosahedron
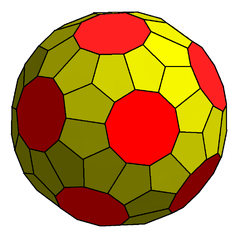
The truncated triakis icosahedron, or more precisely an order-10 truncated triakis icosahedron, is a convex polyhedron with 72 faces: 10 sets of 3 pentagons arranged in an icosahedral arrangement, with 12 decagons in the gaps.
| Truncated triakis icosahedron | |
|---|---|
 | |
| Conway notation | t10kI = dk10tD |
| Faces | 12 decagons 60 pentagons |
| Edges | 210 |
| Vertices | 140 |
| Dual | Decakis truncated dodecahedron |
| Vertex configuration | 12 (5.5.5) 60 (5.5.10) |
| Symmetry group | Ih |
| Properties | convex |
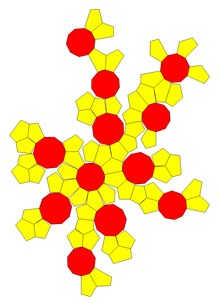 Net | |
Triakis icosahedron
It is constructed from taking a triakis icosahedron by truncating the order-10 vertices. This creates 12 regular decagon faces, and leaves 60 mirror-symmetric pentagons.
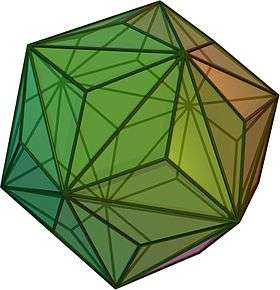 Triakis icosahedron |
Decakis truncated dodecahedron
The dual of the truncated triakis icosahedron is called a decakis truncated dodecahedron. It can be seen as a truncated dodecahedron with decagonal pyramids augmented to the faces.
 Truncated dodecahedron |
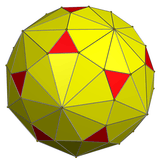 Decakis truncated dodecahedron |
 Net |
gollark: Oh, just make it n-dimensional, that's always fun.
gollark: Exactly!
gollark: Just add more dimensions until it's unique.
gollark: How about BF, but with a *3D* program?
gollark: If your language doesn't specify limited memory somehow, then it is (well, can be) TC even if the implementations don't run on infinite-memory computrons.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.