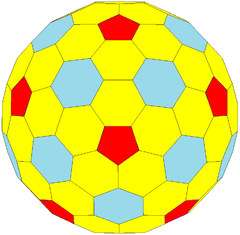
Truncated pentakis dodecahedron
The truncated pentakis dodecahedron is a convex polyhedron constructed as a truncation of the pentakis dodecahedron. It is Goldberg polyhedron GV(3,0), with pentagonal faces separated by an edge-direct distance of 3 steps.
| Truncated pentakis dodecahedron | |
|---|---|
 | |
| Conway notation | tkD |
| Goldberg polyhedron | GPV(3,0) or {5+,3}3,0 |
| Fullerene | C180[1] |
| Faces | 92: 12 pentagons 20+60 hexagons |
| Edges | 270 (2 types) |
| Vertices | 180 (2 types) |
| Vertex configuration | (60) 5.6.6 (120) 6.6.6 |
| Symmetry group | Icosahedral (Ih) |
| Dual polyhedron | Pentahexakis truncated icosahedron |
| Properties | convex |
Related polyhedra
It is in an infinite sequence of Goldberg polyhedra:
| Index | GP(1,0) | GP(2,0) | GP(3,0) | GP(4,0) | GP(5,0) | GP(6,0) | GP(7,0) | GP(8,0)... |
|---|---|---|---|---|---|---|---|---|
| Image |  D |
 kD |
 tkD |
 |
 |
 |
 |
 |
| Duals |  I |
 cD |
 ktI |
 |
 |
gollark: It can't be forked because no.
gollark: I was considering making a config generator to generate the config.
gollark: I only have 600 lines of config.
gollark: Nginx """"works"".
gollark: They made it more annoying so I dropped it.
References
- Deza, A.; Deza, M.; Grishukhin, V. (1998), "Fullerenes and coordination polyhedra versus half-cube embeddings", Discrete Mathematics, 192 (1): 41–80, doi:10.1016/S0012-365X(98)00065-X, archived from the original on 2007-02-06.
- Antoine Deza, Michel Deza, Viatcheslav Grishukhin, Fullerenes and coordination polyhedra versus half-cube embeddings, 1998 PDF
External links
- VTML polyhedral generator Try "tkD" (Conway polyhedron notation)
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.