Troppy effect

Troppy effect – a phenomenon of formation of irregular residual surface wave-like damages resulting from a non-stationary process of cyclic elastoplastic deformation in the zone of contact at rolling friction. It was openly and studied by professor L. A. Sosnovskiy with staff in the framework of Tribo-Fatigue.[1][2][3][4][5][6][7][8]

Physics of the phenomenon

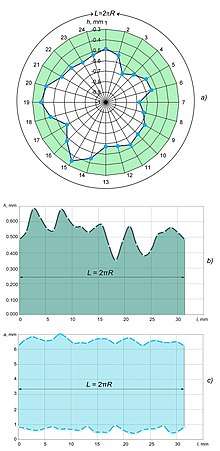
The troppy effect is a result of the loss of stability of the roller movement along the shaft due to the accumulation of residual wear-fatigue damage at loads exceeding the rolling fatigue limit. The loss of motion stability is characterized by self-excitation of vibrations in the roller / shaft system and is accompanied by elastoplastic deformation of bodies in the contact area. Under certain conditions, it leads to the appearance of an unsteady vibro-shock process with a variable frequency and repeatedly variable contact load. This leads to the formation of residual wave-like damages on the contact surfaces with half-barrel-shaped dimples, the sizes of which in the circumferential, axial and radial directions turn out to be unequal (Figure 1). Sources (cause) of oscillations in three directions are, firstly, distortions of the contact geometry and, secondly, local non-isotropy of the mechanical properties of the material in different contact zones. A significant role is also played by fretting fatigue in the main directions (circumferential and axial) of the contact plane.

Figure 1 – Typical radial residual deformations (a) and their scan along the circumference L=2πR (b); c – axial residual deformations

Among the numerous and diverse phenomena of loss of stability of motion, we can distinguish those in which disturbing motion factors are due to the complex interaction of elements (in the general case of a different nature) of the mechanical system. Such, for example, are flutter and shimmy, the description of which was given in the works of M. V. Keldysh[9]. In addition to the design features of the wing (flutter) and aircraft landing gear (shimmy), their loss of stability during movement occurs as a result of a special kind of interaction either with the air flow (with flutter) or with the ground (with shimmy). Although the phenomenon of troppy is on a par with the phenomena of flutter and shimmy in the complexity of the nature of the interaction, nevertheless, troppy has significant features. Firstly, in the tribo-fatigue system, two solid deformable bodies interact. Secondly, for troppy, the history of movement and loading (damage to the elements of the tribo-fatigue system) is important, which determines the change in the conditions of interaction over time. If during flutter and shimmy the disturbing factors are external to the mechanical system and do not depend on it, then during troppy the disturbing factors are determined by the mechanical parameters of the system, which change during movement and damage. In other words, the inverse effect of motion on disturbing factors is realized.

Troppy effect in real systems

The troppy effect can be regarded as fundamental; in practice, its particular species are found. So, for example, under certain operating conditions of rails and railway wheels, similar irregular damages of both elements are formed, which initiate strong vibrations of the rolling stock, and sometimes the train goes off the rails[10][11][12]. Such damage was found, for example, on the rails of tram lines and railways (Figure 2). The analysis shows that in systems such as tire / road, gears similar damages also occur in severe operating conditions. A peculiar realization of the troppy effect is a forest or meadow path; it is this image that underlies the name of the effect.

Figure 2 – Wave-like rail damage

Troppy model

The troppy model was developed by Professor S. S. Sherbakov[5][7][8]

The following representations are the basis of the theoretical solution of the troppy problem:

  • stresses caused by contact and non-contact loads in the roller / shaft system act simultaneously in a single area;
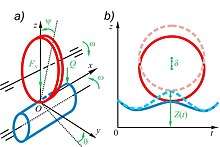
  • during the movement, excitation of the oscillations of the roller in the xz, xy planes and along the z axis is possible (Figure 3);
  • as a result of the loss of stability of motion, the basic parameters of the Hertz contact change: the dimensions of the semiaxes a and b of the contact ellipse, the largest pressure p0 in the center of the contact, the convergence of the δ axes;
  • loss of motion stability over time can also be initiated by a change in local mechanical properties on the rolling track;
  • in the general case, the description of the conditions for the loss of stability of motion takes into account both the action of disturbing force factors and the time variation of the geometric dimensions in the contact area; these changes may result from permanent deformations.
Figure 3 – Calculated schemes

The system of equations of motion under conditions of troppy, taking into account the gyroscopic moment, has the form:

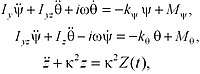
where Iy, Iz, Iyz respectively, the moments of inertia of the roller relative to the axes y and z and the centrifugal moment, i is the moment of inertia of the roller relative to its axis of rotation, and force factors

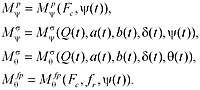
According to the presented model, the non-stationary process of deformation under the analyzed conditions is accompanied by fluctuations in all contact parameters, as well as contact pressure.

Experimental study

An experimental study of the troppy effect was conducted with the participation of Ph.D. S. A. Tyurin and V. A. Yakovlev[13][14]

The troppy effect was experimentally studied in laboratory conditions on SI-series machines when testing tribo-fatigue roller / shaft systems for mechano-rolling fatigue (Figure 4, see the test scheme). In the working zone, both cyclic stresses occur during volumetric deformation (bending by load Q) and the contact stress field under contact load FN.

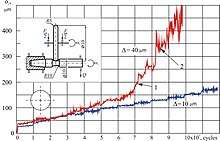
Figure 4 – Influence of the error in the manufacture of the shaft on the excitation of the troppy during mechano-rolling fatigue

The mechano-rolling fatigue tests were subjected to the tribo-fatigue system steel 25HGT (roller) / steel 45 (shaft). A characteristic feature of this system was that the strength of the shaft metal is significantly less than that of the roller, therefore, during the tests, residual deformations and damage are found only in the vicinity of the roller track on the shaft, while the dimensions of the roller remain almost undistorted. The influence of the manufacturing error of the shaft on the excitation of the troppy is shown in the graphs of Figure 4. For deviations of Δ=10 μm, the movement of the roller along the shaft was stable during the entire test period. But if the manufacturing error was Δ=40 μm, there was a loss of motion stability (see mark 1 in Figure 4). The development of wave-like residual damage leads to a shock-fatigue process (see mark 2 in Figure 4). This process is unsteady in amplitude and frequency. Consequently, the geometry of the elements and the accuracy in contact are factors that largely form the conditions for the occurrence of residual wave-like damage during mechano-rolling fatigue tests.

In the case of an initial local violation of the shaft geometry (flat on its surface – see Figure 5), the movement of the roller along the shaft is practically unsteady initially. And this unsteadiness is enhanced due to the residual change in the size of the contact area and the local properties of the material along the rolling track. This is due to the fact that after the jump on the flat, the roller impacts the metal in the vicinity of the next point 2. Next, a similar process of the formation of wave-like damages occurs already in the vicinity of point 3. It turns out that the residual wave-like damage rolls from point to point. When the shock-fatigue process begins, they are formed along the entire length of the rolling track during a very short test time and become deep and wide.

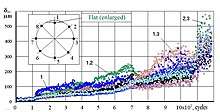
Figure 5 – Change in the convergence of the δc axes in time with rolling fatigue of a friction shaft (steel 45) / roller (steel 25HGT): values at 8 points (1, 2, ..., 8) along the circumference of the shaft L=2πR

The role of the anisotropy of the mechanical properties of the material at different points along the shaft circumference on the excitation of vibrations in the system is shown in Figure 6. The first scan of the shaft circumference without contact load (FN=0) was obtained after 1,129 rotation cycles. Further, the family of such scans is given depending on the values of FN and N (measurements were carried out at six marked points). It is clearly seen that the influence of the anisotropy of the local properties of the metal is detected at FN=100 and 200 H after N=50,000 cycles.

Figure 6 – Effect of local anisotropy of material properties

Figure 7, a shows photographs of residual surface wave-like damage in the vicinity of the shaft roller track. In the case when the roller and shaft are made of the same steel and have the same surface properties, residual wave-like damages under certain test conditions are formed on the working surfaces of both elements simultaneously (see Figure 7, b).

Figure 7 – The nature of damage to the shaft (a) and roller (b) after mechano-rolling fatigue tests

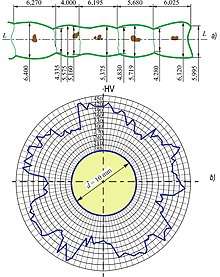
Figure 8 shows that when the troppy effect is realized under the conditions of the experiments, the surface hardness on the rolling track varies from 330 to 450 HV, i.e. by 36 %. And the value of relative plastic deformation reaches 62 %.

Figure 8 – Surface residual wave-like damage (pitting holes are blackened) (a) and the distribution of microhardness along the length L=2πR of the shaft raceway (b)
gollark: --remind 5m test
gollark: Did that one work correctly? Oh, right, real autobotrobot.
gollark: --remind 0m test
gollark: What *is* it doing? Bees this utterly.
gollark: Consistency.

References
  1. Sosnovskiy, L. A. "Troppy Phenomenon" / L. A. Sosnovskiy, S. S. Shcharbakou // Proc. of World Tribology Congress III [Electronic resource] : Washington, D.C. USA, September 12–16, 2005. – Washington, 2005.
  2. Sosnovskiy, L. A. "Troppy Phenomenon" (CM104) / L. A. Sosnovskiy, S. S. Sherbakov. – Proceedings of 7th International Conference on Contact Mechanics and Wear of Rail / Wheel Systems (Brisbane, Australia, Sept. 24–27, 2006). – Brisbane. – 2006. – V. 1. – P. 115–125.
  3. Sosnovskiy, L.A. Tribo-Fatigue. Wear-Fatigue Damage and Its Prediction / L.A. Sosnovskiy // Series : Foundations of Engineering Mechanics, Springer, 2005. – P. 228–230.
  4. 摩擦疲劳学 磨损 – 疲劳损伤及其预测. L.A. 索斯洛-夫斯基著, 高万振译 – 中国矿业大学出版社, 2013. – 324 p.
  5. Sosnovskiy, L. A. "Vibro-Impact in Rolling Contact" / L. A. Sosnovskiy, S. S. Sherbakov // Journal of Sound and Vibration. – 2007. – № 308. – P. 489–503.
  6. Sosnovskiy, L. A. Wear-fatigue mechanics / L. A. Sosnovskiy. – Gomel : BelSUT, 2007. – 434 p. (in Russian).
  7. Sosnovskiy, L. A. Surprises of Tribo-Fatigue / L. A. Sosnovskiy, S. S. Sherbakov. – Minsk : Magic Book, 2009. – 200 p.
  8. Sherbakov, S. S. "Theoretical and experimental studies of the troppy phenomenon / S. S. Sherbakov // Tribo-Fatigue : proc. of VI Intern. Symposium on Tribo-Fatigue ISTF 2010, Minsk, oct. 25 – Nov. 1, 2010. : in 2 p. / Belarusian State University ; ed. board. : M. A. Zhuravkov (prev.) [et al.]. – Minsk : BSU Press, 2010. – V. 2. – P. 233–242. (in Russian).
  9. Keldysh, M. V. "Shimmy during the movement of the wheel of a three-wheeled chassis" / M. V. Keldysh // Selected Works. Mechanics. – M .: Nauka, 1985. – P. 491–530. (in Russian).
  10. Alias, J. "Characteristics of wave formation in rails" / J. Alias // Rail International. – 1986. November. – P. 17–23.
  11. "Combating the roaring-rail by grinding using a mobile train formation" // Rail Engineering International. – 1972. February-March, – Vol. 2. – № 2. – P. 81–86.
  12. Hampton, R. D. "Rail corrugation – experience of US transit properties" // R. D. Hampton // Transp. Res. Rec. – 1986. – № 1071. – P. 16–18.
  13. Tyurin, S. A. Mechano-rolling fatigue : research methods and general laws : Ph. D. thesis : 01.02.06 / S. A. Tyurin. – Gomel : BelSUT, 2003
  14. Yakovlev, V. A. About one criterion of the limiting state in mechano-rolling fatigue / V. A. Yakovlev, L. A. Sosnovsky, S. A. Tyurin // Modern Problems of Engineering: Materials of the Intern. scientific and technical conf. - Gomel: GSTU named after P.O. Sukhoi, 2000. - V. 1. - P. 177–179.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.