Trilinear polarity

In geometry, trilinear polarity is a certain correspondence between the points in the plane of a triangle not lying on the sides of the triangle and lines in the plane of the triangle not passing through the vertices of the triangle. "Although it is called a polarity, it is not really a polarity at all, for poles of concurrent lines are not collinear lines."[1] It was Poncelet (1788–1867), a French engineer and mathematician, who introduced the idea of the trilinear polar of a point in 1865.[1][2]

Definitions
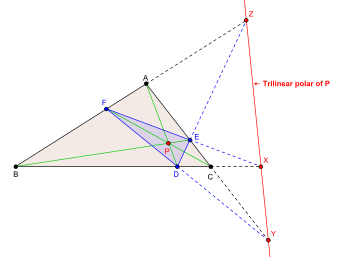
Diagram illustrating the definition of the trilinear polar of a point.

Let ABC be a plane triangle and let P be any point in the plane of the triangle not lying on the sides of the triangle. Briefly, the trilinear polar of P is the axis of perspectivity of the cevian triangle of P and the triangle ABC.

In detail, let the line AP, BP, CP meet the sidelines BC, CA, AB at D, E, F respectively. Triangle DEF is the cevian triangle of P with reference to triangle ABC. Let the pairs of line (BC, EF), (CA, FD), (DE, AB) intersect at X, Y, Z respectively. By Desargues' theorem the points X, Y, Z are collinear. The line of collinearity is the axis of perspectivity of triangle ABC and triangle DEF. The line XYZ is the trilinear polar of the point P.[1]

The points X, Y, Z can also be obtained as the harmonic conjugates of D, E, F with respect to the pairs of points (B,C), (C, A), (A, B) respectively. Poncelet used this idea to define the concept of trilinear polars.[1]

If the line L is the trilinear polar of the point P with respect to the reference triangle ABC then P is called the trilinear pole of the line L with respect to the reference triangle ABC.

Trilinear equation

Let the trilinear coordinates of the point P be (p : q : r). Then the trilinear equation of the trilinear polar of P is[3]

x / p + y / q + z / r = 0.

Construction of the trilinear pole
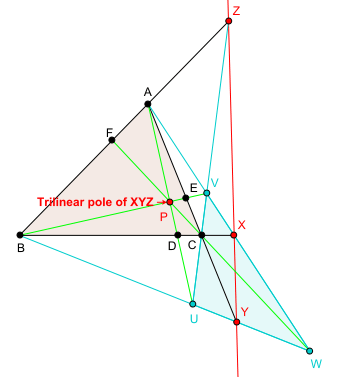
Diagram illustrating the construction of the trilinear pole of a given line XYZ

Let the line L meet the sides BC, CA, AB of triangle ABC at X, Y, Z respectively. Let the pairs of lines (BY, CZ), (CZ, AX), (AX, BY) meet at U, V, W. Triangles ABC and UVW are in perspective and let P be the center of perspectivity. P is the trilinear pole of the line L.

Some trilinear polars

Some of the trilinear polars are well known.[4]

  • The trilinear polar of the centroid of triangle ABC is the line at infinity.
  • The trilinear polar of the symmedian point is the Lemoine axis of triangle ABC.
  • The trilinear polar of the orthocenter is the orthic axis.
  • Trilinear polars are not defined for points coinciding with the vertices of triangle ABC.

Poles of pencils of lines
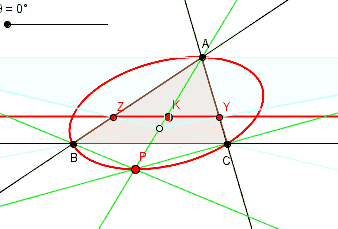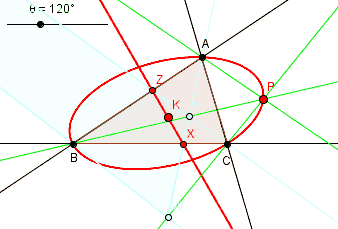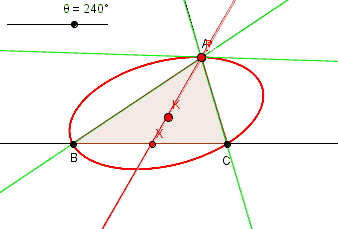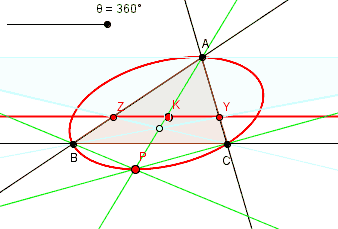
Animation illustrating the fact that the locus of the trilinear poles of a pencil of lines passing through a fixed point K is a circumconic of the reference triangle.

Let P with trilinear coordinates ( X : Y : Z ) be the pole of a line passing through a fixed point K with trilinear coordinates ( x0 : y0 : z0 ). Equation of the line is

  • x / X + y / Y + z / Z =0.

Since this passes through K,

  • x0 / X + y0 / Y + z0 / Z =0.

Thus the locus of P is

  • x0 / x + y0 / y + z0 / z =0.

This is a circumconic of the triangle of reference ABC. Thus the locus of the poles of a pencil of lines passing through a fixed point is a circumconic of the triangle of reference.

gollark: Many things are on Netflix.
gollark: Ah yes, stop using what's basically the cleanest power source which is actually practical while carbon dioxide emissions are a huge problem, intelligence 1000.
gollark: I kind of want to know what stuff got deleted now...
gollark: <@128643042537111552> Incognito mode just stops your *browser* from putting stuff in the history on *your computer*. It stops absolutely nobody else.
gollark: Because of stupid political stuff nobody seems to actually want to *fix* that sort of problem, and politicians just go "More good things! Less bad things! Outgroup bad!".

References
  1. Coxeter, H.S.M. (1993). The Real Projective Plane. Springer. pp. 102–103. ISBN 9780387978895.
  2. Coxeter, H.S.M. (2003). Projective Geometry. Springer. pp. 29. ISBN 9780387406237.
  3. Weisstein, Eric W. "Trilinear Polar". MathWorld—A Wolfram Web Resource. Retrieved 31 July 2012.
  4. Weisstein, Eric W. "Trilinear Pole". MathWorld—A Wolfram Web Resource. Retrieved 8 August 2012.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.