Traffic bottleneck

A traffic bottleneck is a localized disruption of vehicular traffic on a street, road, or highway. As opposed to a traffic jam, a bottleneck is a result of a specific physical condition, often the design of the road, badly timed traffic lights, or sharp curves. They can also be caused by temporary situations, such as vehicular accidents.

Bottleneck caused by construction.

Bottlenecks can also occur in other methods of transportation. Capacity bottlenecks are the most vulnerable points in a network and are very often the subject of offensive or defensive military actions. Capacity bottlenecks of strategic importance - such as the Panama Canal where traffic is limited by the infrastructure - are normally referred to as choke points; capacity bottlenecks of tactical value are referred to as mobility corridors.

Causes

Traffic bottlenecks are caused by a wide variety of things:

• Construction zones where one or more existing lanes become unavailable (as depicted in the diagram on the right)
• Accident sites that temporarily close lanes
• Narrowing a low-capacity highway road
• Terrain (e.g., uphill sections, very sharp curves)
• Poorly timed traffic lights
• Slow vehicles that disrupt upstream traffic flow upstream (also known as a "moving bottleneck")
• Rubbernecking

Rubbernecking is an example of how bottlenecks can be induced by psychological factors; for example, vehicles safely pulled to the shoulder by a police car often result in passing drivers to slow down to "get a better look" at the situation.

Graphical and theoretical representation

Traffic flow theory can be used to model and represent bottlenecks.

Stationary bottleneck

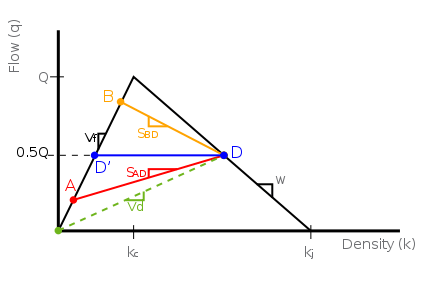
Consider a stretch of highway with two lanes in one direction. Suppose that the fundamental diagram is modeled as shown here. The highway has a peak capacity of Q vehicles per hour, corresponding to a density of k_c vehicles per mile. The highway normally becomes jammed at k_j vehicles per mile.

Before capacity is reached, traffic may flow at A vehicles per hour, or a higher B vehicles per hour. In either case, the speed of vehicles is v_f (or "free flow"), because the roadway is under capacity.

Now, suppose that at a certain location x₀, the highway narrows to one lane. The maximum capacity is now limited to D’, or half of Q, since only one lane of the two is available. State D shares the same flow rate as state D', but its vehicular density is higher.

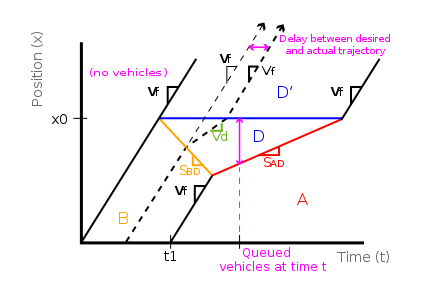
Using a time-space diagram, we may model the bottleneck event. Suppose that at time t₀, traffic begins to flow at rate B and speed v_f. After time t₁, vehicles arrive at the lighter flowrate A.

Before the first vehicles reach location x₀, the traffic flow is unimpeded. However, downstream of x₀, the roadway narrows, reducing the capacity by half—and to below that of state B. Due to this, vehicles will begin queuing upstream of x₀. This is represented by high-density state D. The vehicle speed in this state is the slower v_d, as taken from the fundamental diagram. Downstream of the bottleneck, vehicles transition to state D', where they again travel at free-flow speed v_f.

Once vehicles arrive at rate A starting at time t₁, the queue will begin to clear and eventually dissipate. State A has a flowrate below the one-lane capacity of states D and D'.

On the time-space diagram, a sample vehicle trajectory is represented with a dotted arrow line. The diagram can readily represent vehicular delay and queue length. It's a simple matter of taking horizontal and vertical measurements within the region of state D.

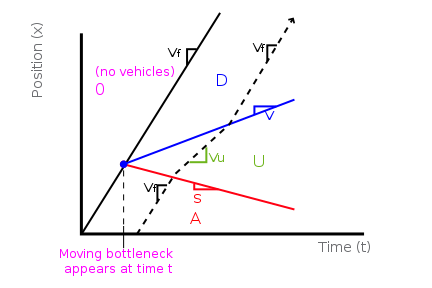
Dynamic bottleneck

A slow tractor creates a moving bottleneck.

For this example, consider three lanes of traffic in one direction. Assume that a truck starts traveling at speed v, more slowly than at the free-flow speed v_f. As shown on the fundamental diagram below, speed q_u represents the reduced capacity (two-thirds of Q, i.e., 2 out of 3 lanes available) around the truck.

State A represents normal approaching traffic flow, again at speed v_f. State U, with flowrate q_u, corresponds to the queuing upstream of the truck. On the fundamental diagram, vehicle speed v_u is slower than speed v_f. But once drivers have navigated around the truck, they can again speed up and transition to downstream state D. While this state travels at free flow, the vehicle density is less because fewer vehicles get around the bottleneck.

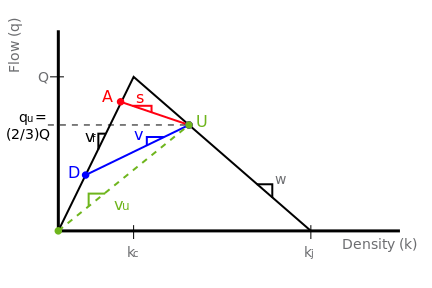
Suppose that, at time t, the truck slows from the free-flow rate to v. A queue builds behind the truck, represented by state U. Within the region of state U, vehicles more slowly, as indicated by the sample trajectory. Because state U limits to a smaller flow than state A, the queue will back up behind the truck and eventually crowd out the entire highway (slope s is negative). If state U had the higher flow, there would still be a growing queue. However, it would not back up because the slope s would be positive.[1]

Identifying Bottlenecks

In recent articles, percolation theory has been applied to study traffic congestion in a city. The quality of the global traffic in a city at a given time is by a single parameter, the percolation critical threshold. The critical threshold represent the velocity below which one can travel in a large fraction of city network. The method is able to identify repetitive traffic bottlenecks.[2] Critical exponents characterizing the cluster size distribution of good traffic are similar to those of percolation theory.[3]     An empirical study regarding the size distribution of traffic jams has been performed recently by Zhang et al[4] . They found an approximate universal power law for the jam sizes distribution.

See also

• Choke point
• Kerner’s breakdown minimization principle
• Three-phase traffic theory
• Traffic congestion
• Traffic congestion: Reconstruction with Kerner’s three-phase theory

References

1. Daganzo, Robert, ed. (1997). Fundamentals of Transportation and Transportation Operations. Pergamon-Elsevier, Oxford, UK
2. Li, Daqing; Fu, Bowen; Wang, Yunpeng; Lu, Guangquan; Berezin, Yehiel; Stanley, H. Eugene; Havlin, Shlomo (2015). "Percolation transition in dynamical traffic network with evolving critical bottlenecks". Proceedings of the National Academy of Sciences. 112 (3): 669–672. Bibcode:2015PNAS..112..669L. doi:10.1073/pnas.1419185112. ISSN 0027-8424. PMC 4311803. PMID 25552558.
3. G Zeng, D Li, S Guo, L Gao, Z Gao, HE Stanley, S Havlin (2019). "Switch between critical percolation modes in city traffic dynamics". Proceedings of the National Academy of Sciences. 116 (1): 23–28. doi:10.1073/pnas.1801545116.CS1 maint: multiple names: authors list (link)
4. Limiao Zhang, Guanwen Zeng, Daqing Li, Hai-Jun Huang, H Eugene Stanley, Shlomo Havlin (2019). "Scale-free resilience of real traffic jams". Proceedings of the National Academy of Sciences. 116 (18): 8673–8678. doi:10.1073/pnas.1814982116.CS1 maint: multiple names: authors list (link)