T-coloring
In graph theory, a T-Coloring of a graph , given the set T of nonnegative integers containing 0, is a function that maps each vertex to a positive integer (color) such that if u and w are adjacent then .[1] In simple words, the absolute value of the difference between two colors of adjacent vertices must not belong to fixed set T. The concept was introduced by William K. Hale.[2] If T = {0} it reduces to common vertex coloring.
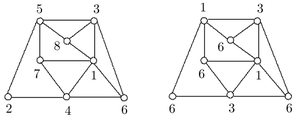
The T-chromatic number, is the minimum number of colors that can be used in a T-coloring of G.
The complementary coloring of T-coloring c, denoted is defined for each vertex v of G by
where s is the largest color assigned to a vertex of G by the c function.[1]
Relation to Chromatic Number
- Proposition. .[3]
Proof. Every T-coloring of G is also a vertex coloring of G, so Suppose that and Given a common vertex k-coloring function using the colors We define as
For every two adjacent vertices u and w of G,
so Therefore d is a T-coloring of G. Since d uses k colors, Consequently,
T-span
The span of a T-coloring c of G is defined as
The T-span is defined as:
Some bounds of the T-span are given below:
- For every k-chromatic graph G with clique of size and every finite set T of nonnegative integers containing 0,
- For every graph G and every finite set T of nonnegative integers containing 0 whose largest element is r, [5]
- For every graph G and every finite set T of nonnegative integers containing 0 whose cardinality is t, [5]
See also
References
- Chartrand, Gary; Zhang, Ping (2009). "14. Colorings, Distance, and Domination". Chromatic Graph Theory. CRC Press. pp. 397–402.
- W. K. Hale, Frequency assignment: Theory and applications. Proc. IEEE 68 (1980) 1497–1514.
- M. B. Cozzens and F. S. Roberts, T -colorings of graphs and the Channel Assignment Problem. Congr. Numer. 35 (1982) 191–208.
- Chartrand, Gary; Zhang, Ping (2009). "14. Colorings, Distance, and Domination". Chromatic Graph Theory. CRC Press. p. 399.
- M. B. Cozzens and F. S. Roberts, T -colorings of graphs and the Channel Assignment Problem. Congr. Numer. 35 (1982) 191–208.