Symmetry element

A symmetry element is a point of reference about which symmetry operations can take place. In particular, symmetry elements can be identities, mirror planes, axes of rotation (both proper and improper), and centers of inversion.[1] A symmetry element corresponds to a symmetry operation that generates the same representation of an object.

Identity

The identity symmetry element is found in all objects and is denoted E.[2] It corresponds to an operation of doing nothing to the object.

Mirror planes
Main article: Reflection (mathematics)

Mirror planes are denoted by σ. In particular, a vertical mirror plane is denoted σv.

Rotational symmetry
Main article: Rotational symmetry

Rotational symmetry, also known as radial symmetry, is represented by an axis about which the object rotates in its corresponding symmetry operation. A group of proper rotations is denoted as Cn, where n is the order of rotation.[3]. The Cn notation is also used for the related, more abstract, cyclic group. An improper rotation is the composition of a rotation about an axis and a reflection in a plane perpendicular to that axis. It's group is denoted by Sn.

Inversion
Main article: Point reflection

For inversion, denoted i, there must be a point in the center of an object that is the inversion center. In the inversion operation for 3D coordinates, the inversion center is the origin (0,0,0). When an object is inverted, the position vector of a point in an object, ⟨x,y,z⟩, is inverted to ⟨-x,-y,-z⟩.

  • Example of vertical mirror plane.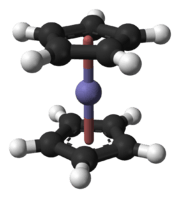
  • Ferrocene molecule, an example of S10 symmetry element.
gollark: EACH PERSON gives each option a score of 0 to 5, I mean, and they're all summed up.
gollark: You give each option an arbitrary score from 0 to 5 or something and whichever gets the highest total wins.
gollark: That idea of resource allocation doesn't seem very good, though.
gollark: Although score voting is simple too and apparently might be better.
gollark: Yes, I know how approval voting works.

See also

References
  1. Robert G. Mortimer (10 June 2005). Mathematics for Physical Chemistry. Academic Press. pp. 276–. ISBN 978-0-08-049288-9.
  2. Glazer, Michael; Burns, Gerald; Glazer, Alexander. Space groups for solid state scientists.
  3. Glazer, Michael; Burns, Gerald; Glazer, Alexander. Space groups for solid state scientists.


This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.