Studentized range distribution

In probability and statistics, studentized range distribution is the continuous probability distribution of the studentized range of an i.i.d. sample from a normally distributed population.

Studentized range distribution

Probability density function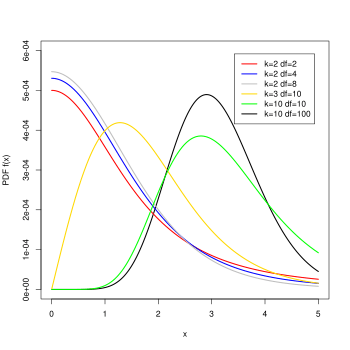
Cumulative distribution function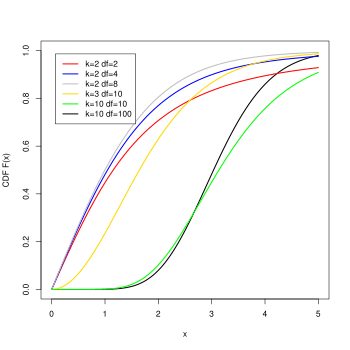
Parameters	k > 1, the number of groups ${\displaystyle \nu }$ > 0, the degrees of freedom
Support	${\displaystyle q\in (0,+\infty )}$
PDF	${\displaystyle {\begin{matrix}f_{\text{R}}(q;k,\nu )={\frac {\,{\sqrt {2\pi \,}}\,k\,(k-1)\,\nu ^{\nu /2}\,}{\Gamma (\nu /2)\,2^{\left(\nu /2-1\right)}}}\int _{0}^{\infty }s^{\nu }\,\varphi ({\sqrt {\nu \,}}\,s)\,\times \\[0.5em]\left[\int _{-\infty }^{\infty }\varphi (z+q\,s)\,\varphi (z)\,\left[\Phi (z+q\,s)-\Phi (z)\right]^{k-2}\,\mathrm {d} z\right]\,\mathrm {d} s\end{matrix}}}$
CDF	${\displaystyle {\begin{matrix}F_{\text{R}}(q;k,\nu )={\frac {\,{\sqrt {2\pi \,}}\,k\,\nu ^{\nu /2}\,}{\,\Gamma (\nu /2)\,2^{\left(\nu /2-1\right)}}}\int _{0}^{\infty }s^{\nu -1}\,\varphi ({\sqrt {\nu \,}}\,s)\,\times \\[0.5em]\qquad \left[\int _{-\infty }^{\infty }\varphi (z)\,\left[\Phi (z+q\,s)-\Phi (z)\right]^{k-1}\,\mathrm {d} z\right]\,\mathrm {d} s\end{matrix}}}$

Suppose that we take a sample of size n from each of k populations with the same normal distribution N(μ, σ²) and suppose that ${\displaystyle {\bar {y}}_{\min }}$ is the smallest of these sample means and ${\displaystyle {\bar {y}}_{\max }}$ is the largest of these sample means, and suppose s² is the pooled sample variance from these samples. Then the following random variable has a Studentized range distribution.

${\displaystyle q={\frac {{\overline {y}}_{\max }-{\overline {y}}_{\min }}{s/{\sqrt {n\,}}}}}$

Definition

Probability density function

Differentiating the cumulative distribution function with respect to q gives the probability density function.

${\displaystyle f_{\text{R}}(q;k,\nu )={\frac {{\sqrt {2\pi \,}}\,k\,(k-1)\,\nu ^{\nu /2}}{\Gamma (\nu /2)\,2^{\left(\nu /2-1\right)}}}\int _{0}^{\infty }s^{\nu }\,\varphi ({\sqrt {\nu \,}}\,s)\,\left[\int _{-\infty }^{\infty }\varphi (z+q\,s)\,\varphi (z)\,\left[\Phi (z+q\,s)-\Phi (z)\right]^{k-2}\,\mathrm {d} z\right]\,\mathrm {d} s}$

Note that in the outer part of the integral, the equation

${\displaystyle \varphi ({\sqrt {\nu \,}}\,s)\,{\sqrt {2\pi \,}}=e^{-\left(\nu \,s^{2}/2\right)}}$

was used to replace an exponential factor.

Cumulative distribution function

The cumulative distribution function is given by [1]

${\displaystyle F_{\text{R}}(q;k,\nu )={\frac {{\sqrt {2\pi \,}}\,k\,\nu ^{\nu /2}}{\,\Gamma (\nu /2)\,2^{(\nu /2-1)}\,}}\int _{0}^{\infty }s^{\nu -1}\varphi ({\sqrt {\nu \,}}\,s)\left[\int _{-\infty }^{\infty }\varphi (z)\left[\Phi (z+q\,s)-\Phi (z)\right]^{k-1}\,\mathrm {d} z\right]\,\mathrm {d} s}$

Special cases

If k is 2 or 3,[2] the studentized range probability distribution function can be directly evaluated, where ${\displaystyle \varphi (z)}$ is the standard normal probability density function and ${\displaystyle \Phi (z)}$ is the standard normal cumulative distribution function.

${\displaystyle f_{R}(q;k=2)={\sqrt {2\,}}\,\varphi \left(\,q/{\sqrt {2\,}}\right)}$

${\displaystyle f_{R}(q;k=3)=6{\sqrt {2\,}}\,\varphi \left(\,q/{\sqrt {2\,}}\right)\left[\Phi \left(q/{\sqrt {6\,}}\right)-{\tfrac {1}{2}}\right]}$

When the degrees of freedom approaches infinity the studentized range cumulative distribution can be calculated for any k using the standard normal distribution.

${\displaystyle F_{R}(q;k)=k\,\int _{-\infty }^{\infty }\varphi (z)\,{\Bigl [}\Phi (z+q)-\Phi (z){\Bigr ]}^{k-1}\,\mathrm {d} z=k\,\int _{-\infty }^{\infty }\,{\Bigl [}\Phi (z+q)-\Phi (z){\Bigr ]}^{k-1}\,\mathrm {d} \Phi (z)}$

Uses

Critical values of the studentized range distribution are used in Tukey's range test.

The studentized range is used to calculate significance levels for results obtained by data mining, where one selectively seeks extreme differences in sample data, rather than only sampling randomly.

Derivation of the studentized range distribution function

The studentized range distribution function arises from re-scaling the sample range R by the sample standard deviation s, since the studentized range is customarily tabulated in units of standard deviations, with the variable q = ​^R⁄_s . The derivation begins with a perfectly general form of the distribution function of the sample range, which applies to any sample data distribution.

In order to obtain the distribution in terms of the "studentized" range q, we will change variable from R to s and q. Assuming the sample data is normally distributed, the standard deviation s will be χ distributed. By further integrating over s we can remove s as a parameter and obtain the re-scaled distribution in terms of q alone.

General form

For any probability density function f_X, the range probability density f_R is:[2]

${\displaystyle f_{R}(r;k)=k\,(k-1)\int _{-\infty }^{\infty }f_{X}\left(t+{\tfrac {1}{2}}r\right)f_{X}\left(t-{\tfrac {1}{2}}r\right)\left[\int _{t-{\tfrac {1}{2}}r}^{t+{\tfrac {1}{2}}r}f_{X}(x)\,\mathrm {d} x\right]^{k-2}\,\mathrm {d} \,t}$

What this means is that we are adding up the probabilities that, given k draws from a distribution, two of them differ by r, and the remaining k − 2 draws all fall between the two extreme values. If we change variables to u where ${\displaystyle u=t-{\tfrac {1}{2}}r}$ is the low-end of the range, and define F_X as the cumulative distribution function of f_X, then the equation can be simplified:

${\displaystyle f_{R}(r;k)=k\,(k-1)\int _{-\infty }^{\infty }f_{X}(u+r)\,f_{X}(u)\,\left[\,F_{X}(u+r)-F_{X}(u)\,\right]^{k-2}\,\mathrm {d} \,u}$

We introduce a similar integral, and notice that differentiating under the integral-sign gives

${\displaystyle {\begin{aligned}{\frac {\partial }{\partial r}}&\left[k\,\int _{-\infty }^{\infty }f_{X}(u)\,{\Bigl [}\,F_{X}(u+r)-F_{X}(u)\,{\Bigr ]}^{k-1}\,\mathrm {d} \,u\right]\\[5pt]={}&k\,(k-1)\int _{-\infty }^{\infty }f_{X}(u+r)\,f_{X}(u)\,{\Bigl [}\,F_{X}(u+r)-F_{X}(u)\,{\Bigr ]}^{k-2}\,\mathrm {d} \,u\end{aligned}}}$

which recovers the integral above,[lower-alpha 1] so that last relation confirms

${\displaystyle {\begin{aligned}F_{R}(r;k)&=k\int _{-\infty }^{\infty }f_{X}(u){\Bigl [}\,F_{X}(u+r)-F_{X}(u)\,{\Bigr ]}^{k-1}\,\mathrm {d} \,u\\&=k\int _{-\infty }^{\infty }{\Bigl [}\,F_{X}(u+r)-F_{X}(u)\,{\Bigr ]}^{k-1}\,\mathrm {d} \,F_{X}(u)\end{aligned}}}$

because for any continuous cdf

${\displaystyle {\frac {\partial F_{R}(r;k)}{\partial r}}=f_{R}(r;k)}$

Special form for normal data

The range distribution is most often used for confidence intervals around sample averages, which are asymptotically normally distributed by the central limit theorem.

In order to create the studentized range distribution for normal data, we first switch from the generic f_X and F_X to the distribution functions φ and Φ for the standard normal distribution, and change the variable r to s·q, where q is a fixed factor that re-scales r by scaling factor s:

${\displaystyle f_{R}(q;k)=s\,k\,(k-1)\int _{-\infty }^{\infty }\varphi (u+sq)\varphi (u)\,\left[\,\Phi (u+sq)-\Phi (u)\right]^{k-2}\,\mathrm {d} u}$

Choose the scaling factor s to be the sample standard deviation, so that q becomes the number of standard deviations wide that the range is. For normal data s is chi distributed[lower-alpha 2] and the distribution function f_S of the chi distribution is given by:

${\displaystyle f_{S}(s;\nu )\,\mathrm {d} s={\begin{cases}{\dfrac {\nu ^{\nu /2}\,s^{\nu -1}e^{-\nu \,s^{2}/2}\,}{2^{\left(\nu /2-1\right)}\Gamma (\nu /2)}}\,\mathrm {d} s&{\text{for }}\,0<s<\infty ,\\[4pt]0&{\text{otherwise}}.\end{cases}}}$

Multiplying the distributions f_R and f_S and integrating to remove the dependence on the standard deviation s gives the studentized range distribution function for normal data:

${\displaystyle f_{R}(q;k,\nu )={\frac {\nu ^{\nu /2}\,k\,(k-1)}{2^{\left(\nu /2-1\right)}\Gamma (\nu /2)}}\int _{0}^{\infty }s^{\nu }e^{-\nu s^{2}/2}\int _{-\infty }^{\infty }\varphi (u+sq)\,\varphi (u)\,\left[\,\Phi (u+sq)-\Phi (u)\right]^{k-2}\,\mathrm {d} u\,\mathrm {d} s}$

where

q is the width of the data range measured in standard deviations,

ν is the number of degrees of freedom for determining the sample standard deviation,[lower-alpha 3] and

k is the number of separate averages that form the points within the range.

The equation for the pdf shown in the sections above comes from using

${\displaystyle e^{-\nu \,s^{2}/2}={\sqrt {2\pi \,}}\,\varphi ({\sqrt {\nu \,}}\,s)}$

to replace the exponential expression in the outer integral.

Notes

1. Technically, the relation is only true for points ${\displaystyle u}$ where ${\displaystyle f_{X}(u+r)>0}$, which holds everywhere for normal data as discussed in the next section, but not for distributions whose support has an upper bound, like uniformly distributed data.
2. Note well the absence of "squared": The text refers to the χ distribution, not the χ² distribution.
3. Usually ${\displaystyle \nu =n-1}$, where n is the total number of all datapoints used to find the averages that are the values in the range.

References

1. Lund, R.E.; Lund, J.R. (1983). "Algorithm AS 190: Probabilities and upper quantiles for the studentized range". Journal of the Royal Statistical Society. 32 (2): 204–210. JSTOR 2347300.
2. McKay, A.T. (1933). "A note on the distribution of range in samples of n". Biometrika. 25 (3): 415–420. doi:10.2307/2332292. JSTOR 2332292.

• Pearson, E.S.; Hartley, H.O. (1942). "The probability integral of the range in samples of N observations from a normal population". Biometrika. 32 (3): 301–310. doi:10.1093/biomet/32.3-4.309. JSTOR 2332134.
• Hartley, H.O. (1942). "The range in random samples". Biometrika. 32 (3): 334–348. doi:10.2307/2332137. JSTOR 2332137.
• Dunlap, W.P.; Powell, R.S.; Konnerth, T.K. (1977). "A FORTRAN IV function for calculating probabilities associated with the studentized range statistic". Behavior Research Methods & Instrumentation. 9 (4): 373–375. doi:10.3758/BF03202264.