Structural fracture mechanics
Structural fracture mechanics is the field of structural engineering concerned with the study of load-carrying structures that includes one or several failed or damaged components. It uses methods of analytical solid mechanics, structural engineering, safety engineering, probability theory, and catastrophe theory to calculate the load and stress in the structural components and analyze the safety of a damaged structure.
There is a direct analogy between fracture mechanics of solid and structural fracture mechanics:
| Fracture mechanics | Structural fracture mechanics | |
|---|---|---|
| Model | Solid with a crack | Multi-component structure with a failed component |
| Defect driving force | Stress intensity factor | Overload stress |
| System property | Fracture toughness | Reserve ability / Structural robustness |
There are different causes of the first component failure: 1) mechanical overload, fatigue (material), unpredicted scenario, etc. 2) “human intervention” like unprofessional behavior or a terrorist attack.
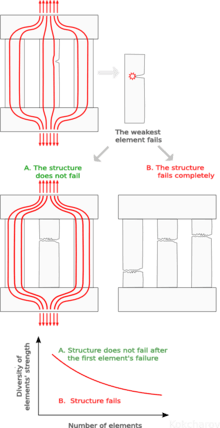
There are two typical scenarios:
A. A localized failure does NOT cause immediate collapse of the entire structure.
B. The entire structure fails immediately after one of its components fails.
If the structure does not collapse immediately there is a limited period of time until the catastrophic structural failure of the entire structure. There is a critical number of structural elements that defines whether the system has reserve ability or not.[1]
Safety engineers use the failure of the first component as an indicator and try to intervene during the given period of time to avoid the catastrophe of the entire structure. For example, “Leak-Before-Break”[2] methodology means that a leak will be discovered prior to a catastrophic failure of the entire piping system occurring in service. It has been applied to pressure vessels, nuclear piping, gas and oil pipelines, etc.
The methods of structural fracture mechanics are used as checking calculations to estimate sensitivity of a structure to its component failure.[3]
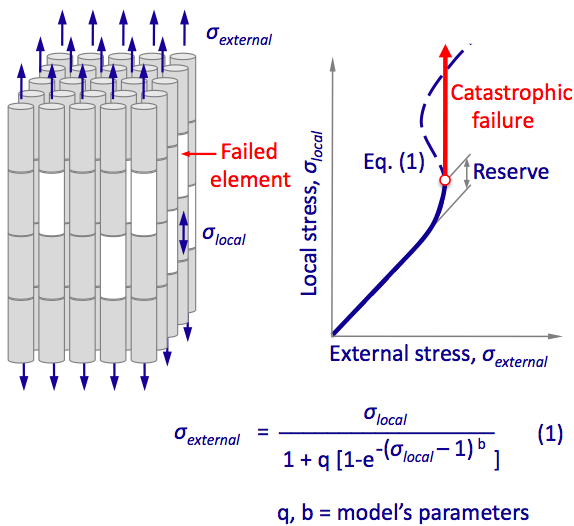
The failure of a complex system with parallel redundancy can be estimated based on probabilistic properties of the system elements. The model[4] supposes that failure of several elements causes neighboring elements overloading. The model equation (1) shows the relationship between local and external stresses. The equation (1) is similar to the cusp catastrophe behavior. The theory predicts reserve ability of the complex system and the critical external stress.
See also
- Catastrophic failure – Sudden and total failure from which recovery is impossible
- Catastrophe theory – Area of mathematics
- Fracture mechanics – Field of mechanics concerned with the study of the propagation of cracks in materials
- Nuclear safety and security
- Progressive collapse
- Safety engineering – Engineering discipline which assures that engineered systems provide acceptable levels of safety
- Structural integrity and failure – Engineering event in which the structural integrity of a construction is compromised due to failure of components of the structure
References
- Kokcharov I. Reserve ability of parallel system with failed elements. Theoretical and Applied Fracture Mechanics, Volume 48, Issue 3, December 2007, Pages 225-230
- Applicability of the leak before break concept. Report of the IAEA Extrabudgetary Programme on the Safety of WWER-440 Model 230 Nuclear Power Plants, 1993
- Kokcharov I., Burov A. Structural Integrity Analysis. Part 6. Structural Safety. 2013
- Kokcharov I. Failure probability assessment of parallel redundant structures. Theoretical and Applied Fracture Mechanics, Volume 36, Issue 2, September–October 2001, Pages 109-114