Strictly convex space
In mathematics, a strictly convex space is a normed vector space (X, || ||) for which the closed unit ball is a strictly convex set. Put another way, a strictly convex space is one for which, given any two distinct points x and y on the unit sphere ∂B (i.e. the boundary of the unit ball B of X), the segment joining x and y meets ∂B only at x and y. Strict convexity is somewhere between an inner product space (all inner product spaces being strictly convex) and a general normed space in terms of structure. It also guarantees the uniqueness of a best approximation to an element in X (strictly convex) out of a convex subspace Y, provided that such an approximation exists.
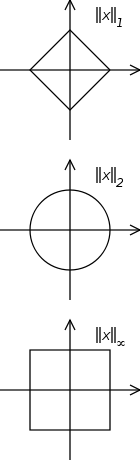
If the normed space X is complete and satisfies the slightly stronger property of being uniformly convex (which implies strict convexity), then it is also reflexive by Milman-Pettis theorem.
Properties
The following properties are equivalent to strict convexity.
- A normed vector space (X, || ||) is strictly convex if and only if x ≠ y and || x || = || y || = 1 together imply that || x + y || < 2.
- A normed vector space (X, || ||) is strictly convex if and only if x ≠ y and || x || = || y || = 1 together imply that || αx + (1 − α)y || < 1 for all 0 < α < 1.
- A normed vector space (X, || ||) is strictly convex if and only if x ≠ 0 and y ≠ 0 and || x + y || = || x || + || y || together imply that x = cy for some constant c > 0;
- A normed vector space (X, || ||) is strictly convex if and only if the modulus of convexity δ for (X, || ||) satisfies δ(2) = 1.
References
- Goebel, Kazimierz (1970). "Convexity of balls and fixed-point theorems for mappings with nonexpansive square". Compositio Mathematica. 22 (3): 269–274.