Star product

In mathematics, the star product is a method of combining graded posets with unique minimal and maximal elements, preserving the property that the posets are Eulerian.

Not to be confused with the Moyal product, also sometimes referred to as the star product.

Definition

The star product of two graded posets ${\displaystyle (P,\leq _{P})}$ and ${\displaystyle (Q,\leq _{Q})}$, where ${\displaystyle P}$ has a unique maximal element ${\displaystyle {\widehat {1}}}$ and ${\displaystyle Q}$ has a unique minimal element ${\displaystyle {\widehat {0}}}$, is a poset ${\displaystyle P*Q}$ on the set ${\displaystyle (P\setminus \{{\widehat {1}}\})\cup (Q\setminus \{{\widehat {0}}\})}$. We define the partial order ${\displaystyle \leq _{P*Q}}$ by ${\displaystyle x\leq y}$ if and only if:

1. ${\displaystyle \{x,y\}\subset P}$, and ${\displaystyle x\leq _{P}y}$;

2. ${\displaystyle \{x,y\}\subset Q}$, and ${\displaystyle x\leq _{Q}y}$; or

3. ${\displaystyle x\in P}$ and ${\displaystyle y\in Q}$.

In other words, we pluck out the top of ${\displaystyle P}$ and the bottom of ${\displaystyle Q}$, and require that everything in ${\displaystyle P}$ be smaller than everything in ${\displaystyle Q}$.

Example

For example, suppose ${\displaystyle P}$ and ${\displaystyle Q}$ are the Boolean algebra on two elements.

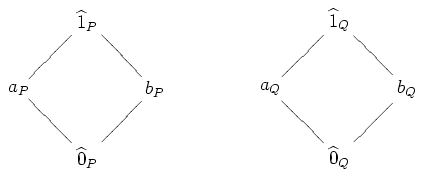
Then ${\displaystyle P*Q}$ is the poset with the Hasse diagram below.

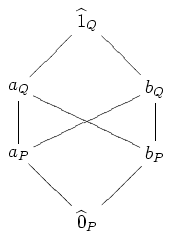
Properties

The star product of Eulerian posets is Eulerian.

See also

• Product order, a different way of combining posets

References

• Stanley, R., Flag ${\displaystyle f}$-vectors and the ${\displaystyle \mathbf {cd} }$-index, Math. Z. 216 (1994), 483-499.

This article incorporates material from star product on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.