Stadium (geometry)

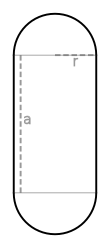
A stadium is a two-dimensional geometric shape constructed of a rectangle with semicircles at a pair of opposite sides.[1] The same shape is known also as a discorectangle,[2] obround,[3][4] or sausage body.[5]

Parameters of a stadium
The Bunimovich stadium, a chaotic dynamical system based on the stadium shape
The bottom of this plastic basket is stadium-shaped.

The shape is based on a stadium, a place used for athletics and horse racing tracks.

A stadium may be constructed as the Minkowski sum of a disk and a line segment.[5] Alternatively, it is the neighborhood of points within a given distance from a line segment. A stadium is a type of oval. However, unlike some other ovals such as the ellipses, it is not an algebraic curve because different parts of its boundary are defined by different equations.

Formulas

The perimeter of a stadium is calculated by the formula where a is the length of the straight sides and r is the radius of the semicircles. With the same parameters, the area of the stadium is .[6]

Bunimovich stadium

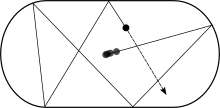
When this shape is used in the study of dynamical billiards, it is called the Bunimovich stadium. Leonid Bunimovich used this shape to show that it is possible for billiard tracks to exhibit chaotic behavior (positive Lyapunov exponent and exponential divergence of paths) even within a convex billiard table.[7]

A capsule is produced by revolving a stadium around the line of symmetry that bisects the semicircles.

gollark: No.
gollark: Desmos is implicitly doing y = f(x) for that line.
gollark: Why does what happen?
gollark: Yes, that is a channel.
gollark: The output is turned into the Y coordinate when plotted like this.

References
  1. "Stadium - from Wolfram MathWorld". Mathworld.wolfram.com. 2013-01-19. Retrieved 2013-01-31.
  2. Dzubiella, Joachim; Matthias Schmidt; Hartmut Löwen (2000). "Topological defects in nematic droplets of hard spherocylinders". Physical Review E. 62: 5081. arXiv:cond-mat/9906388. Bibcode:2000PhRvE..62.5081D. doi:10.1103/PhysRevE.62.5081.
  3. Ackermann, Kurt. "Obround - Punching Tools - VIP, Inc". www.vista-industrial.com. Retrieved 2016-04-29.
  4. "Obround Level Gauge Glass : L.J. Star Incorporated". L.J.Star Incorporated. Archived from the original on 2016-04-22. Retrieved 2016-04-29.
  5. Huang, Pingliang; Pan, Shengliang; Yang, Yunlong (2015). "Positive center sets of convex curves". Discrete & Computational Geometry. 54 (3): 728–740. doi:10.1007/s00454-015-9715-9. MR 3392976.
  6. "Stadium Calculator". Calculatorsoup.com. Retrieved 2013-01-31.
  7. Bunimovič, L. A. (1974). "The ergodic properties of certain billiards". Funkcional. Anal. i Priložen. 8 (3): 73–74. MR 0357736.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.