Spider diagram
In mathematics, a unitary spider diagram adds existential points to an Euler or a Venn diagram. The points indicate the existence of an attribute described by the intersection of contours in the Euler diagram. These points may be joined together forming a shape like a spider. Joined points represent an "or" condition, also known as a logical disjunction.
A spider diagram is a boolean expression involving unitary spider diagrams and the logical symbols . For example, it may consist of the conjunction of two spider diagrams, the disjunction of two spider diagrams, or the negation of a spider diagram.
Example
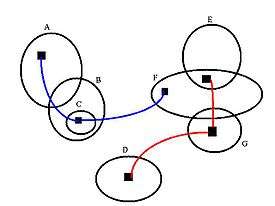
In the image shown, the following conjunctions
In the universe of discourse defined by this Euler diagram, in addition to the conjunctions specified above, all possible sets from A through B and D through G are available separately. The set C is only available as a subset of B. Often, in complicated diagrams, singleton sets and/or conjunctions may be obscured by other set combinations.
The two spiders in the example correspond to the following logical expressions:
- Red spider:
- Blue spider:
References
- Howse, J. and Stapleton, G. and Taylor, H. Spider Diagrams London Mathematical Society Journal of Computation and Mathematics, (2005) v. 8, pp. 145–194. ISSN 1461-1570 Accessed on January 8, 2012 here
- Stapleton, G. and Howse, J. and Taylor, J. and Thompson, S. What can spider diagrams say? Proc. Diagrams, (2004) v. 168, p. 169–219. Accessed on January 4, 2012 here
- Stapleton, G. and Jamnik, M. and Masthoff, J. On the Readability of Diagrammatic Proofs Proc. Automated Reasoning Workshop, 2009. PDF
External links
| Wikimedia Commons has media related to Spider diagrams. |