Slepian–Wolf coding

In information theory and communication, the Slepian–Wolf coding, also known as the Slepian–Wolf bound, is a result in distributed source coding discovered by David Slepian and Jack Wolf in 1973. It is a method of theoretically coding two lossless compressed correlated sources.[1]

Problem setup

Distributed coding is the coding of two, in this case, or more dependent sources with separate encoders and a joint decoder. Given two statistically dependent i.i.d. finite-alphabet random sequences ${\displaystyle X^{n}}$ and ${\displaystyle Y^{n}}$, the Slepian–Wolf theorem gives a theoretical bound for the lossless coding rate for distributed coding of the two sources.

Theorem

The bound for the lossless coding rates as shown below:[1]

${\displaystyle R_{X}\geq H(X|Y),\,}$

${\displaystyle R_{Y}\geq H(Y|X),\,}$

${\displaystyle R_{X}+R_{Y}\geq H(X,Y).\,}$

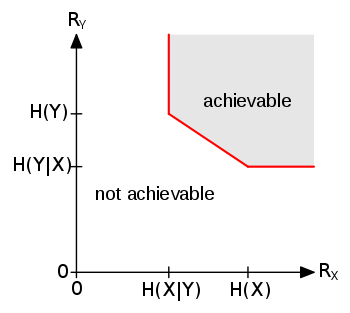
If both the encoder and the decoder of the two sources are independent, the lowest rate it can achieve for lossless compression is ${\displaystyle H(X)}$ and ${\displaystyle H(Y)}$ for ${\displaystyle X}$ and ${\displaystyle Y}$ respectively, where ${\displaystyle H(X)}$ and ${\displaystyle H(Y)}$ are the entropies of ${\displaystyle X}$ and ${\displaystyle Y}$. However, with joint decoding, if vanishing error probability for long sequences is accepted, the Slepian–Wolf theorem shows that much better compression rate can be achieved. As long as the total rate of ${\displaystyle X}$ and ${\displaystyle Y}$ is larger than their joint entropy ${\displaystyle H(X,Y)}$ and none of the sources is encoded with a rate smaller than its entropy, distributed coding can achieve arbitrarily small error probability for long sequences.[1]

A special case of distributed coding is compression with decoder side information, where source ${\displaystyle Y}$ is available at the decoder side but not accessible at the encoder side. This can be treated as the condition that ${\displaystyle R_{Y}=H(Y)}$ has already been used to encode ${\displaystyle Y}$, while we intend to use ${\displaystyle H(X|Y)}$ to encode ${\displaystyle X}$. In other words, two isolated sources can compress data as efficiently as if they were communicating with each other. The whole system is operating in an asymmetric way (compression rate for the two sources are asymmetric).[1]

This bound has been extended to the case of more than two correlated sources by Thomas M. Cover in 1975,[2] and similar results were obtained in 1976 by Aaron D. Wyner and Jacob Ziv with regard to lossy coding of joint Gaussian sources.[3]

See also

• Data compression
• Data synchronization
  • Synchronization (computer science)
• DISCUS
• Timeline of information theory

References

1. Slepian & Wolf 1973, pp. 471–480.
2. Cover 1975, pp. 226–228.
3. Wyner & Ziv 1976, pp. 1–10.

Sources

• Cover, Thomas M. (March 1975). "A proof of the data compression theorem of Slepian and Wolf for ergodic sources" by T.". IEEE Transactions on Information Theory. 21 (2): 226–228. doi:10.1109/TIT.1975.1055356. ISSN 0018-9448.CS1 maint: ref=harv (link)
• Slepian, David S.; Wolf, Jack K. (July 1973). "Noiseless coding of correlated information sources". IEEE Transactions on Information Theory. 19 (4): 471–480. doi:10.1109/TIT.1973.1055037. ISSN 0018-9448.CS1 maint: ref=harv (link)
• Wyner, Aaron D.; Ziv, Jacob (January 1976). "The rate-distortion function for source coding with side information at the decoder". IEEE Transactions on Information Theory. 22 (1): 1–10. CiteSeerX 10.1.1.137.494. doi:10.1109/TIT.1976.1055508. ISSN 0018-9448.CS1 maint: ref=harv (link)

External links

• Wyner-Ziv Coding of Video algorithm for video compression that performs close to the Slepian–Wolf bound (with links to source code).